
I see that Erik Lentz (Göttingen University) has just begun a personal blog, something that may begin to attract attention given that Dr. Lentz has offered up a new paper on faster than light travel. At the moment, the blog is bare-bones, listing only the paper itself (citation below) and an upcoming online talk that may be of interest. Here’s what the Lentz blog has on this:
Upcoming online talk to be given on 18 March 2021 at 3pm Eastern Standard Time for the Science Speaker Series at the Jim and Linda Lee Planetarium: https://youtu.be/6O8ji46VBK0
I checked the URL and found the page with a countdown timer, so I assume the event is publicly accessible. I would imagine it will draw a number of curious scientists and lay-people.
On the subject of faster than light travel, much of the work in the journals has evolved from Miguel Alcubierre’s now well known paper “The Warp Drive: Hyper-fast travel within general relativity,” which presented the idea of a ‘bubble’ of spacetime within which a volume of flat space could exist. In other words, it might be possible to enclose a spacecraft within such a bubble. While there is a physical restriction on objects within spacetime moving faster than the speed of light, spacetime itself is theoretically capable of expansion without limit — this is essentially the notion of ‘inflation’ that drives most current thinking about the earliest moments of the universe.
Alcubierre’s paper ran in May, 1994 in the prestigious journal Classical and Quantum Gravity, a venue whose demanding standards of peer review and acceptance give it high credibility. In other words, papers in this journal rightfully attract attention because of the demanding requirements of publication. I had more or less overlooked the new paper by Dr. Lentz until I realized that it was published here, after which I began to take notice.
This does not mean, of course, that either the Alcubierre ‘warp drive’ concept or the much different ideas of Erik Lentz can ever be engineered, but it does offer a great deal of interest from the standpoint of the mathematics of warped spacetime. After the Alcubierre paper, much of the ongoing work has been involved in exploring how negative energy operates, for ‘negative energy density’ is exotic and vast amounts would be required to form the needed ‘bubble’ of spacetime. The Lentz paper does away with negative energy. I’m hearing it described as an idea more in conformance with conventional physics, though that may also need clarification.
The essential notion put forward by Dr. Lentz is that there are configurations of spacetime curvature that can be explored as ‘solitons,’ which are a solution he deems physically viable, and thus not dependent on negative energy at all. Here we’re already in deep water. A soliton, as I have been learning, is a wave that can retain its shape and move at constant velocity. That such curiosities are within the realm of physical possibility is made clear by the origin of the study of solitons. They actually go back to an observation by British engineer John S. Russell in 1834. In a famous and oft-quoted passage delivered ten years later to the British Association for the Advancement of Science, Russell had this to say about what he called a ‘wave of translation’:
I was observing the motion of a boat which was rapidly drawn along a narrow channel by a pair of horses, when the boat suddenly stopped – not so the mass of water in the channel which it had put in motion; it accumulated round the prow of the vessel in a state of violent agitation, then suddenly leaving it behind, rolled forward with great velocity, assuming the form of a large solitary elevation, a rounded, smooth and well-defined heap of water, which continued its course along the channel apparently without change of form or diminution of speed. I followed it on horseback, and overtook it still rolling on at a rate of some eight or nine miles an hour, preserving its original figure some thirty feet long and a foot to a foot and a half in height. Its height gradually diminished, and after a chase of one or two miles I lost it in the windings of the channel. Such, in the month of August 1834, was my first chance interview with that singular and beautiful phenomenon which I have called the Wave of Translation.
Thus was born the study of solitons, which now extends into nuclear physics, optics and other fields, now including exotic propulsion. Notice that what Russell describes is a wave that is stable and can travel. His use of the word ‘translation’ means that this is not a wave made up of the same water that travels the length of the channel he was observing, but rather a wave that moves through the medium. Water is moving but being displaced in the process. We can think of the wave of translation — or at least I’ve seen it referred to this way — as a ‘wave packet’ that can maintain its shape, as it did in Scotland’s Union Canal for Russell.
I turned to Hilborn and Cross’ Chaos and Nonlinear Dynamics (Oxford University Press, 2000) to see solitons described as ‘nonlinear wave phenomena.’ Thus:
A soliton is a spatially localized wave disturbance that can propagate over long distances without changing itsshape. In brief, many nonlinear spatial modes become synchronized to produce a stable localized disturbance.
Solitons turn out to be remarkably stable. A great deal of mathematics has gone on since as solition concepts evolved, all much beyond my pay grade. I looked again at Dr. Lentz’ website to get a notion of what he was proposing in his own words, because I find it hard to make the considerable jump from the early observations of Russell to today’s understanding of solitons. Here’s Lentz with a vest-pocket description of faster than light travel that does not violate Einsteinian relativity:
Hyper-fast (as in faster than light) solitons within modern theories of gravity have been a topic of energetic speculation for the past three decades. One of the most prominent critiques of compact mechanisms of superluminal motion within general relativity is that the geometry must largely be sourced from a form of negative energy density, though there are no such known macroscopic sources in particle physics. I was recently able [to] disprove this position by constructing a new class of hyper-fast soliton solutions within general relativity that are sourced purely from positive energy densities, thus removing the need for exotic negative-energy-density sources. This is made possible through considering hyperbolic relations between components of the space-time metric’s shift vector. Further, these solutions are sourceable by a classical electronic plasma, placing superluminal phenomena into the purview of known physics. This is a very exciting breakthrough that I hope to have more [to] report on soon.
I take this to mean that there are mathematical solutions for spacetime curvature that use solitons as the mode of organization. Alcubierre’s ‘warp bubble’ becomes, in soliton mode, a wave that maintains its shape and moves at constant velocity. The key here, Lentz believes, is that this is a way of altering spacetime geometry without the use of exotic negative energy. Moreover, Lentz’ equations evidently show that tidal forces within the bubble can be minimized. The passage of time inside the soliton can be adjusted to match the time outside the bubble.
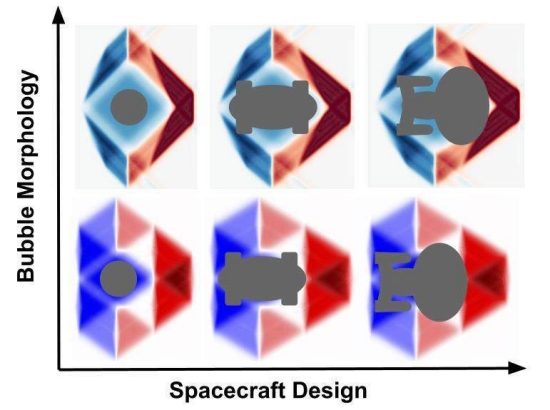
Image: Artistic impression of different spacecraft designs considering theoretical shapes of different kinds of “warp bubbles.” Credit: E Lentz.
We would still need enormous amounts of energy, but we are dealing with the kind of energy we understand rather than the far more amorphous ‘negative energy.’ Here’s Lentz again:
“The energy required for this drive travelling at light speed encompassing a spacecraft of 100 meters in radius is on the order of hundreds of times of the mass of the planet Jupiter. The energy savings would need to be drastic, of approximately 30 orders of magnitude to be in range of modern nuclear fission reactors… Fortunately, several energy-saving mechanisms have been proposed in earlier research that can potentially lower the energy required by nearly 60 orders of magnitude.”
Such energy savings methods would be prodigious indeed and it is to these that Dr. Lentz apparently turns next. The paper is Lentz, “Breaking the Warp Barrier: Hyper-Fast Solitons in Einstein-Maxwell-Plasma Theory,” Classical and Quantum Gravity Vol. 38, No. 7 (March, 2021). Abstract. We are in very deep mathematical waters here, so all I want to do is point to the paper and urge those interested to take in Dr. Lentz’ talk on the 18th.



While 100m spacecraft is very Str Trek, I would be happy if it could push 1gm spacecraft faster than light. How much energy is needed for that?FTL communication systems (pushing memory chips) could hold a KIII civilization together reducing the time delays for coordination. If this is possible, are these solitons detectable?
You just described a WMD, with emphasis on the M.
As a semi-pro writer, I’ve long admired, and frequently sought to emulate (!) Paul’s unique and invariably charming writing style. This morning I had to laugh out loud! Paul wrote
We can now add ‘massive understatement’ to Paul’s toolkit.
Deep and getting deeper, Michael!
And the deep water is glowing blue, from Cerenkov radiation (due to particles exceeding the speed of light–in water)!
I’m curious how it doesn’t violate Special Relativity. That was an issue with the original Alcubierre Warp Drive – if you could get it to work, then you have a time machine capable of going backwards in time.
I am not sure this is entirely correct in the sense it is often invoked. Going FTL is still moving forward in time, but an observer appears to see events arriving in reverse, apparently violating causality. A starship traveling FTL would appear to arrive from nowhere, then at the same time appear to be traveling in reverse to its point of origin. If it stopped instantaneously to the observer, both the arrived ship and the image of the ship traveling backwards would be seen.
The linking of FTL with time travel in special relativity has to do with a feature of the theory called the “relativity of simultaneity”, which says that different inertial frames disagree about which sets of events happened “simultaneously” at the same time-coordinate, along with another feature, the first of the two basic “postulates of special relativity”, which says all laws of physics work the same (obey the same equations) in all inertial frames.
The math of the relativity of simulataneity works out so that if you could have a signal which moved FTL but forward in time in one inertial frame, it would always be possible to find another inertial frame which defines simultaneity in a different way such that the signal moved back in time in that frame (the event of the signal being received happened at an earlier time than the event of it being sent). And the first postulate of relativity implies that if it’s possible to have a signal that moves back in time in one inertial frame, this must be possible in all inertial frames.
By itself, a lone FTL signal moving in one direction won’t lead to any causal loops (which is what physicists mean by causality violations). But because of these two features of the theory, the existence of FTL would imply that a setup involving two FTL signals going in opposite directions, sent by FTL transmitters at rest in different inertial frames, could create a causal loop. The basic idea is that you have two transmitters A and B moving away from each other at some large fraction of the speed of light, and A sends a signal that moves FTL in A’s rest frame but backwards in time in B’s rest frame, and after receiving it B sends a reply that moves FTL in B’s frame but backwards in time in A’s frame, and the net result is that A gets the reply from B before the moment that A sent the signal in the first place. See the “tachyonic antitelephone” for details: https://en.wikipedia.org/wiki/Tachyonic_antitelephone
Something similar turns out to be true for the Alcubierre warp bubble solution — a single bubble moving in one direction doesn’t create any causality violations, but if you have two bubbles passing each other in opposite directions it can violate causality (as demonstrated in the paper at http://exvacuo.free.fr/div/Sciences/Dossiers/Time/A%20E%20Everett%20-%20Warp%20drive%20and%20causality%20-%20prd950914.pdf ). So I suspect that Lentz’s solution, if it does genuinely allow for FTL travel, could also violate causality in a properly constructed scenario involving two bubbles passing by one another in opposite directions.
Sure so that makes FTL space battles much more lively. Han shot first but backwards in time ?
Any kind of FTL solution is going to need universal editing of excluded collapse States using something like sum over histories more globally than we are used to.
Special Relativity says, no object can travel faster than light through spacetime. This restriction is not applicable to spacetime itself. General Relativity allows space itself to expand, contract or mover faster than light. Here, the Spacetime bubble itself is moving..not the spaceship within it. The ship is at rest inside the bubble (or may be moving with subluminal velocity) with respect to the bubble. Hence it’s not violating Special Relativity.
I mail a letter in an FTL envelope. At the destination the envelope is opened and discarded. The letter followed a non-time like curve. Yes, that does violate SR. The envelope doesn’t change that result, and its consequent effects.
True, but Special Relativity deals with a specific set of circumstances (non rotating, non accelerating reference frames) withing General Relativity. GR does allow for FTL movement, as long as it is only observed to happen for objects at some distance from the observer – GR deals with rotating reference frames, for example, and if I spin around (rotate my reference frame) the Moon can legitimately be considered to have taken and FTL movement in my rotating frame. So, yes and no: We are talking about something that violates SR, but it is occurring in a set of circumstances SR doesn’t cover – they’re covered by GR, and GR does allow such things to happen, within certain conditions.
“the Moon can legitimately be considered to have taken and FTL movement in my rotating frame”
No! Not even close. There is no relative motion. There is no FTL in this context, nor can there be. Angular momentum has nothing to do with this, nor is GR required for the scenario you posed.
But general relativity does need to be able to account for the motion of distant objects in a rotating reference frame – or would you expect that Einstein never considered such frames? This is literally the standard, textbook, way general relativity works, such as this example here: https://link.springer.com/chapter/10.1007/3-540-27700-5_8 . The speed of light is only invariant in inertial frames, in non-inertial frames the speed of light is only locally invariant – ie you cannot see an object directly approach you at speeds greater than c, but you can se an object pass you by at such a speed – compared to the value of c on a path that does directly approach you at least. In the case of a distant object in a spinning frame (to stick to the previous example) those criteria are satisfied, and causality preserved: The distant object never overtakes any light rays, in any reference frame – in the rotating frame it has exceeded c, but so have all light rays that approach it, by the same amount, and in the objects own, inertial, frame it is at rest, and all light rays that directly approach it are moving at c.
Perhaps a better way (and still totally valid) to describe it for you would be that there are two definitions of velocity in General relativity: Proper velocity and co-ordinate velocity. Proper velocity is motion through a co-ordinate system and cannot exceed c, but co-ordinate velocity is motion i/of/i a co-ordinate system and can exceed c. The motion of a distant object. in a rotating frame, and the motion due to expanding or contracting space-time in things like inflation theory and the Alcubierre metric are examples of
co-ordinate velocity.
Apologies for the duff punctuation, grammar and formatting – I was typing with a 4 year old on my lap who wanted to join in!
“but you can se an object pass you by at such a speed”
As I first guessed, this is the nub of your misconception. I’ll give you a simpler example of the same phenomenon. You ought to understand this before leaping into deeper water.
I have a laser pointer. I point it skyward. I then sweep it across the sky. At some distant point the light beam can be said to be traveling FTL. Except, *nothing* is traveling FTL. Not mass, not energy.
Think about it. This is a wave phenomenon akin to group velocity of light whereby features of the wave appear to travel FTL although no photon is doing so. This is relevant to the Lentz paper currently under discussion.
If I understand you aright, that is the opposite scenario to observing a distant object in an inertial frame from within a rotating (or otherwise non-inertial) frame: You, holding the laser pointer, are observing from an inertial reference frame, while the laser pen swung in an arc is in a non-inertial frame. As you are in an inertial frame GR is effectively the same as SR, and doesn’t predict you’d see any FTL motion at a distance (plus the laser pointer photons are on a path that passes through the observer, so it doubly wouldn’t). The difference between wave phase velocity and group velocity is a distinction you then have to make because of that.
That’s all consistent with GR as normally interpreted, and gives rise to what you say about group vs phase velocity, but it has no effect on how an observer i/in/i a rotating reference frame sees things: You are – if i understand right – giving a counter example involving an observer in a non rotating reference frame. So, with respect, I think you’ve effectively got your reference frames mixed up.
I am, perhaps, not explaining myself super well, as this is a well accepted and non-controversial part of GR. I am working directly from the textbooks on GR, if that helps at all, and there’s lots about this on university physics websites. The University of California, among many others, has a fairly accessible bit of text on the subject, so perhaps it would be better if I point towards that? https://math.ucr.edu/home/baez/physics/Relativity/SR/rotatingCoordinates.html
The most relevant quote is:
“If we spin around on the spot, we see the Moon move around us in a huge circle, so isn’t it travelling faster than light in our frame? It is travelling faster than the tabulated value of “c”, but it is not travelling faster than light in its locality; after all, we agree that light is still escaping from its surface. In the language of special relativity, the Moon’s world line always remains within its local light cone; it remains “timelike”. In fact, this behaviour is no different to the well-accepted and well-understood behaviour of light in a uniformly accelerated frame, where the measured speed of light depends upon where in that frame it currently is. This speed can in fact have any value, from zero to infinity. (See the FAQ entry Do moving clocks always run slowly? for further discussion of this.) It’s only in inertial frames that light’s speed is postulated to have the value “c”. ”
…but I’d recommend reading the whole thing so it is in proper context.
I am very familiar with Baez’s work, and I have a shelf full of GR texts. At this point I have nothing to add that will help you with your misconception. Nothing in these examples is moving FTL.
Hey, my response to that would just be the quote I already gave – at this point I’m literally just going to end up referring you to the same mainstream sources and reasoning. If you don’t find them explicitly and repeatedly saying things like “…the measured speed of light depends upon where in that [uniformly accelerating] frame it currently is. This speed can in fact have any value, from zero to infinity….” reason to not hold c as a cut-and-dried absolute to all viewpoints and reference frames described by GR… then I’m happy to agree to disagree. If you enjoy having the last word please do so with my blessing.
We’re getting nowhere, and I really have nothing to add. Yes, rotation is non-inertial, and it certainly messes with measurements. SR describes it perfectly; GR is superfluous in this context. And, again, nothing is moving FTL. Believe what you wish.
That gave a me a double take, so apologies for breaking my promise, but honesty compels me to make clear: Yes, you can do an analysis of a non inertial frame in SR, although the main method I was taught is to treat an accelerating frame as a series of non-accelerating frames and integrate. I apologise for giving the impression I am asserting that you flat out cannot – although IMHO it is much less awkward in GR- and I admit, on re-reading, what I’ve said above could be taken that way.
However I’m afraid I stand by my position here: Doing such an SR analysis of a non-inertial frame yields the same result : The speed of light is only locally invariant, non-local objects may be seen to exceed the local value of C. This is not merely a measurement error, it is a result of there being no preferred reference frame, and is consistent with the basic postulates of relativity:
1: The laws of physics are the same in all i/inertial/i frames of reference.
2: The speed of light in free space has the same value in all i/inertial/i frames of reference in all directions.
OK, honour satisfied I really will butt out now.
Further clarification: There are no preferred frames in GR – inertial frames i/are i/preferred over non-inertial frames in SR, which leads to some motions and forces in an SR analysis of a non-inertial frame having to be excused (defined, if you prefer) as “due to things outside the frame”, hence why GR is usually i/preferred/i for analysing non-inertial frames (including rotating frames) – but, yes, to reiterate: A valid SR analysis of a rotating or accelerating frame can be done.
What do you mean by “moving FTL”? GR has a concept of local inertial frames (only defined in the infinitesimal neighborhood of a point in spacetime) and it’s still true that nothing can move FTL as measured by such a local frame. But GR also allows for arbitrary non-inertial coordinate systems covering large regions of space time (in fact any coordinate system covering a non-infinitesimal region of curved spacetime must be non-inertial). And in such a coordinate system, the coordinate speed (change in coordinate position divided by coordinate time) of a real physical object at one location can be faster than the coordinate system of a light beam at a different location in a non-inertial coordinate system, as is true in Schwarzschild coordinates for example (this is even true for non-inertial coordinate systems in SR, see ‘Rindler coordinates’ where a light beam gets slower and slower, approaching a speed of zero, as it approaches the ‘Rindler horizon’ in this coordinate system). Do you disagree with anything I’m saying here? If not, I think this is all that John was saying as well.
What is FTL in the context I’m using it? Go higher up and read my comments since I thought I was quite clear about it and I didn’t bother repeating my words again and again.
You never defined what coordinate system you were using to define FTL motion–exclusively local inertial frames, or other types of non-inertial coordinate systems as well? Note that I am not talking about phenomenon like laser pointer spots and shadows, only distinct massive particles (of known types, not tachyons) or other massive objects–do you disagree these can have a greater coordinate velocity than light beams in non-inertial coordinate systems like Rindler coordinates?
It’s the light cone you forgot to mention. Nothing can go faster than light according SR. Anything outside the light cone would be faster than light but only a warp drive can do that. Spinning your head or even using a spot light does not add anything to the speed of light which always remains the same. The illusion is the spot light beam doesn’t go to a spot in the night sky instantly. One only sees it in local space in the atmosphere, but it still takes one and half seconds to go to the Moon and more than thirty minutes to get to Mars and further. For example pointing the beam at Canis major and then moving it to Canis minor back and forth quickly won’t make it go faster than light.
I use the perfectly ordinary inertial frame. You can indeed measure velocities higher than c in a non-inertial frame, however, there is no space-like curve (FTL). It’s an artifact of doing the measurement under acceleration. Nothing is travelling FTL. Coordinate systems are neither mass nor energy; they are nothing more than (useful) mathematical constructs.
“however, there is no space-like curve (FTL)”
OK, defining FTL as a space-like curve is a clear definition. But in the context of “warp drive” ideas from GR, it’s worth noting that some physicists have defined a different definition of “effective FTL” in asymptotically flat spacetimes, and may casually refer to something like the Alcubierre drive as “FTL” even though it is only effectively FTL. Details can be found at http://cds.cern.ch/record/367460/files/9810026.pdf — I think the basic idea is that in GR there can be locally strongly curved regions of asymptotically flat spacetimes (spacetimes that approach the metric of SR far from the locally curved region), like traversable wormholes and Alcubierre bubbles, with the property that an observer following a time-like curve can travel through the strongly curved region and get from one location to another much faster than a light beam traveling between the same two locations through the flat region. So this observer would have taken an “effectively FTL” trip even without a space-like worldline.
“can travel through the strongly curved region and get from one location to another much faster than a light beam”
I already had a discussion about this towards the bottom of this article’s comments. Have a look.
We are not dealing with glabally flat Minkowsky space here. Spacetime is curved (for the “warp bubble” or “soliton”). SR (as a limit of GR) says, LOCALLY speed of light is constant and the highest. Here, the letter/spacecraft never even moved relative to the bubble frame. It stands still w.r.t. an observer inside “warp bubble” where spacetime is flat. But for an observer outside of the bubble, GR allows FTL travel of the space itself. The faraway galaxies beyond Hubble radius travel faster than light w.r.t. us- because of metric expansion of space (and so they don’t violate SR locally as well). Something similar is happening here. Warp bubble as a curved spacetime structure itself is moving, not the object within it. SR is not applicable in curved spacetime globally but applicable in curved spacetime locally.
Vibration – The 5th Dimension To Redefine Spacetime Measurements.
“Although our collective scientific understanding has made significant progress over the past several decades, there remain several unsolved and important mysteries of a fundamental nature. Theories have explained the physical properties of a particle or a state of a system in terms of position and time by using the 4-vector space-time measurement. However, determining a system’s state along with all the functioning details can be more completely understood by expansion of this 4-vector measurement system as set forth by Einstein. This paper proposes and explains the rationale to consider vibration as the fifth dimension (as an expansion of this 4-vector system), to form a 5-vector continuum with space-time-vibration triad. This theory constitutes a holistic modified paradigm, which the author defines as the “Space-Time-Vibration” (STV) continuum. The author proposes this 5-vector continuum as a natural extension potentially explaining a few gaps in our understanding.”
http://www.internationaljournalssrg.org/IJAP/paper-details?Id=89
On quantum harmonic oscillator being subjected to absolute potential state.
“In a quantum harmonic oscillator (QHO), the energy of the oscillator increases with increased frequency. In this paper, assuming a boundary condition that the product of momentum and position, or the product of energy density and position remains constant in the QHO, it is established that a particle subjected to increasing frequencies becomes gradually subtler to transform into a very high dormant potential energy. This very high dormant potential energy is referred to as ‘like-potential’ energy in this paper. In the process a new wave function is generated. This new function, which corresponds to new sets of particles, has scope to raise the quantum oscillator energy (QOE) up to infinity. It is proposed to show that this high energy does not get cancelled but remainsdormant. Further, it is proposed that the displacement about the equilibrium goes to zero when the vibration of the oscillator stops and then the QOE becomes infinity – this needs further research. The more the QOE, the greater will be the degree of dormancy. A simple mathematical model has been derived here to discuss the possibilities that are involved in the QHO under the above-mentioned boundary conditions.”
https://www.ias.ac.in/describe/article/pram/088/01/0004
That is so far above my head that it reads to me like an Alan Sokal hoax. Or, as Dr. Who (Tom Baker) calls it “bafflegab”. To paraphrase Clarke’s 3rd law, “Any sufficiently advanced technology explanation sounds like gobbledegook.”
Tilted Two Fluids Cosmological Models with Variable G and ? In General Relativity.
“Tilted two fluids cosmological models with variable G and {\Lambda} In General Relativity are presented. Here one fluid is matter field modelling material content of the universe and another fluid is radiation field modelling the cosmic microwave background (CMB). The tiltedness is also considered .To get the deterministic model, we have assumed a supplementary condition where s and n are constants. We have also discussed the behaviours of some physical parameters.”
https://arxiv.org/abs/1704.07107
Take a look at the images in this article, look familiar?
Could we be imbedded in a soliton, could the local group be in a local soliton? Could the Gravitational Lensing or rings around galaxy cluster actually be the effects from the local discrete soliton surrounding the galaxy clusters. This would mean we may be able to blow a soliton to travel thru hyperspace like a ballistic missile from one energy state to another. Could vibration be the 5th Dimension and the way to blow the bubble. This reminds me of the Jules Verne time machine and the shell it formed when traveling thru time.
Correction; H. G. Wells.
Sorry, this has nothing to do with time travel.
While an ersatz variety of forward time travel is possible with time dilation, meaning that under certain conditions one object or a person can experience time slower – and so be fast forward in time.
In the press release:
https://www.uni-goettingen.de/en/3240.html?id=6192
And on Research gate the entire text is free – though have to be requested.
https://bit.ly/3qJG7xs
It’s made entirely clear that time on such a ship would be kept at the same pace as the outside universe.
“To date, even recent research about superluminal (faster-than-light) transport based on Einstein’s theory of general relativity would require vast amounts of hypothetical particles and states of matter that have “exotic” physical properties such as negative energy density. This type of matter either cannot currently be found or cannot be manufactured in viable quantities. In contrast, new research carried out at the University of Göttingen gets around this problem by constructing a new class of hyper-fast ‘solitons’ using sources with only positive energies that can enable travel at any speed. This reignites debate about the possibility of faster-than-light travel based on conventional physics. ”
In short, no time travel involved in this.
Ironically Alcubierre himself published on the arXiv just yesterday – ‘warp drive basics’. Apparently the front edge of his warp bubble acts like an event horizon meaning any erstwhile crew on board a starship within said bubble could not influence the vessel’s pathway . The article proposes a Krasnikov tube as a solution to this -and the time paradox – whereby two parallel trajectories – one outgoing and another separate one returning, are created before the journey begins . All synchronise with starting time and a finite but small travel time there and then back. This would involve knowing the whole warp bubble projection beforehand and still violate the local energy state at various points in that bubble . So unlike the soliton solution it would still require negative energy
While it have been shown that quantum mechanics ‘Action at a Distance’ can be put to use in cryptography.
And then in more recent years have this also demonstrated in the macroscopic world.
Meaning that faster than light communication is remotely possible.
I still have a hard time imagine a spaceship also doing so.
But while Alcubierre’s idea require engineering that do not even seem possible within the kind of machinery we even can imagine – meaning negative energy.
The idea from Erik Lentz using solitons is at least something we can hypothetically imagine the machinery for.
So thank you for this text, it is at least thought provoking to imagine what consequences and opportunities such a technology would provide.
…but sadly only so in the far future.
The spooky action at a distance cannot be used as a way of FTL communication, see related wiki articles. BTW, there are some physicists thinking that dark matter has negative mass, meaning it can have negative energy. However, even if it’s right, we might need to go to intergalactic space for collecting dark matter.
I am sorry to say, but wikipedia is a horrible source of misinformation.
I have tried to get them to correct some absolute nonsensical claims in biology. A quick look an a relevant textbook would show I was right but the errors remain.
Anyway even though not being a specialist in the field I am a little bit ahead of that level anyway. My gedankenexperiment tell me that when it’s possible to influence a process, and when it also have found a use, there might also be others. but as I said in my reply. I do consider it a remote possibility.
While most dark matter might not be baryonic (part of it might be in my opinion) it do not have negative mass, neither negative energy. Gravity work normally on dark matter and also the influx of energy – there’s a thin fog all trough the solar system, with higher concentrations in the Sun and right under our feet inside Earth. There’s been some speculation that part of Earths heating come from the decay of such particles, but as we already know how Earth is heated, I don’t subscribe to ideas that complicate a matter where there’s no problem in our understanding how it work already. In short, while the idea is interesting do belong in fringe science.
Not sure faster than light travel is even remotely possible. Since we have never observed faster-than-light travel with all of our sensitive measuring methods, I suspect we would have discovered super-luminal effects. Also, no faster-than-light phenomenon has ever been observed around neutron stars and black-holes either via plasma effects or gravitational effects.
Even if faster-than-light travel becomes possible, light-speed inertial travel at infinite time dilations for technical reasons would perhaps permit the entire craft to leave our universe, and perhaps our multiverse, all together.
The late great Stephen Hawking conjectured that the end state of our universe is indistinguishable from the big bang. If so, then travel far enough into the future may in a sense enable travel back to the big bang singularity of quantum gravitational analogue but along another temporal dimension.
So, light-speed is a special speed and my undergraduate academic advisor while studying physics at George Mason University would agree with me. My advisor was Dr Ehrlich and he is currently working on a book on super-luminal tachyons of imaginary mass. He was one of the first if not the first to proposed superluminal neutrinos and is probably the world authority on proposed imaginary mass for some species of neutrinos.
However, who knows for sure? Superluminal travel may yet be possible but the speed of light in inertial travel will always have great possibilities.
“My advisor was Dr Ehrlich and he is currently working on a book on super-luminal tachyons of imaginary mass.”
is it a technical or popular book? when does it come out ?
This is a good point. Generally phenomenon created in a laboratory is first observed in nature. Examples are both nuclear fission and fusion. This is also the same reason I’m skeptical of both dark matter and dark energy. Neither of these have been directly observed in nature, nor created in a laboratory.
We have observed their effects. It is as if you are arguing that lightning wasn’t real before we had direct observational data of electrons.
Both the Higgs particle and black holes were hypothesized from theory without any observation of effects. String theory is entirely a construct with no observational effects or evidence.
There are other cases, like knotted DNA, that came from computational experiments and were later observed, but there was no effect that a knotted DNA was (or is) needed for.
I believe there is a host of theoretical ideas, mostly from maths and computations that are now being found when looking for them.
Are you agreeing or disagreeing with me, or did you instead intend to reply to the same comment I replied to?
Your analogy sounds completely backward to me. We have known about lightning like forever, but electrons only a short while in historical time.
There is literally nothing comparable to lightning for dark matter, these “observed effects” can be explained by alternate hypotheses (https://phys.org/news/2019-01-dark-alternative-theory.html) such as gravity operating differently on cosmic scales, some recent papers have discussed this.
Dark matter/energy are accepted as canon but lack any and all empirical evidence other than purported effects. It could be right, but it could also be very wrong, the modern version of luminiferous aether.
Handing out Nobel prizes for it is extremely premature.
Oh my. Are we going to be deluged by MOND aficionados? No, there is no MOND theory that explains *all* the empirical data. Not even close. There appear to be almost as many MOND theories as there are string theories. This is perhaps unsurprising since there are an infinite number of curves that fit a set of data points, and that is all that MOND is.
“Dark matter/energy are accepted as canon…Nobel prizes for it is extremely premature.”
Now you’re being silly. Your religious fervor against, um, orthodoxy, is irrelevant.
Ron S.
Do I need to invoke Milgrom on you? I’m sure he’d happily refute your claim(s) that MOND doesn’t work for all the empirical data. Any particular datum you’re thinking of? We all know that Lambda-CDM only works on the empirical data because it can be tweaked for every situation – so many adjustable parameters, it’s theoretical silly putty. Mold it anyway you want.
Do you believe Milgrom is some kind of magical incantation to be invoked? More sophisticated curve fitting but curve fitting nevertheless.
I’ve read lots of MOND theories/papers and I am really unimpressed since they pretty well come down to stitching together disparate functions on different length scales and carefully adjusted in order to reduce to a single continuously differentiable function. No theoretical framework, just curve fitting.
I had not intended to get into a discussion about this. I have no vested interest other than my general interest and study of the topic. I’ll give Milgrom some credit for at least attempting to incorporate gravitational lensing into his version of MOND, something that is rarely seen.
I am neither pro or con, MOND vs GR and LCDM vs alternatives. I have no relevant religious convictions. I like what works best, and so far GR wins by a very wide margin. Has Milgrom come up with an alternative to GR with respect to gravitational wave radiation? I ask because I pay him no mind and therefore wouldn’t know.
What FTL effects have been observed?
Perhaps you are referring to this: https://en.wikipedia.org/wiki/Superluminal_motion
We have seen FTL…. relatively speaking.
It happens with time dilation.
Gravity affects space-time and therefore, to an outsider, it also affects light.
If 1 year on earth equals to 1 hour near a black hole then for those near the black hole when they study earth they are seeing FTL light relatively speaking.
That is basically the principle of warp bubbles (or warp tunnels??). Compressing/expanding a distance of 10 Light years into a relatively short distance.
So pretty much you are having a localised unidirectional event horizon.
When I first open the Centauri Dreams website today, I thought “oh how exciting, Paul has found the newest entry into faster than light space drives that I most recently came across…!”. Then I realized when I read further that this was involving a another idea concerning FTL possibility then the one that I was most recently reading about!
I came across this paper just recently in a website called Applied Physics which is, I’m guessing, is some kind of private outfit. Any who, the man who is investigating the Alcubierre warp drive also has another approach to that old way of getting from here to there in record time. Here are the links that I have to that website:
https://appliedphysics.org/physical-warp-drives/
https://arxiv.org/pdf/2102.06824.pdf
Interesting article but I don’t think the idea of the soliton is solves any problems of FTL. For one thing gravity waves can have solitons which are positive energy density so the idea is physically sound, however, the problem is the expansion of space. According to the Alcubierre warp drive, negative energy is needed to expand space. From what scientists have observed in nature all positive energy everywhere appears to make gravity waves and the contraction of space. The exception is the so called dark energy of empty space which has positive energy density but negative pressure, but not negative energy. The problem with dark energy which uses positive energy density to expand space is it is not supportable by any evidence, but completely hypothetical, ad hock and arbitrary. I am not saying there is no such thing, and it is seems to violate observations of matter and energy which is why I don’t like the Lambda cold dark matter theory used to explain cosmic inflation. It seems to me more logical to assume that any expansion of space is caused by negative energy. It’s true that there are still more unknows to be answered about physical cosmology so I try keep an open mind.
The generally accepted view that negative energy requires enormous amounts of positive energy is based on it’s extraction from the quantum vacuum zero point energy and energy density of empty space which our best evidence based on black holes and Hawking radiation. There is no evidence that a Casimir cavity has more negative energy than outside it, but only less energy.
There might be a much more energy efficient way to make negative energy with much less positive energy density if we don’t make it by quantum vacuum extraction. We can do that by learning the coupling of the four forces which we don’t yet know, Propulsion physicist Marc G. Millis gave me this idea. I saw him mention it on one of his lectures on youtube. I did this thought experiment where we can convert one force into another and convert one of the other forces or maybe a combination of all the other forces into gravity and anti gravity wave particles without the quantum vacuum extraction of negative energy.
Solitons may or may not be needed in a warp drive, but the long distance idea does not apply to warp drives because the warping of space to make the warp bubble has to be local. In other words, it does not make the space shorter between two points like a worm hole. Furthermore, without negative energy, we can’t have any FTL or any warp bubble for that matter, and there is no FTL without a warp bubble which drags its local space reference frame with it. Negative energy and the Alcubierre warp drive is completely supported by general relativity because it is a designer space warp. Now if there was an expansion caused by positive energy density which has yet to be proven, it would still be subject to general relativity and we would have to make gravitons and gravity waves with some kind of electronic device which has yet to be invented and it would be only some kind of expansive gravity which would take the same energy as it would to make anti gravity waves if we consider gravitons are their own antiparticles. I would be nice to see some more money in gravity control research.
“According to the Alcubierre warp drive, negative energy is needed to expand space.”
See my links above …
I looked this up at https://arxiv.org/pdf/2006.07125.pdf – it looks like it was written to be clear and very approachable to … someone. Not me, but at least Figure 4 is a graph of the hypersurface volume expansion, so I take it the ship contracts space in front of it and expands space behind it as you’d expect, with an odd little bit at the very front that also expands space … I think. He says this comes out of the hyperbolic solution of the equations and given that the paper is accepted I know *I’m* in no position to naysay!
I imagine even the faintest little diagonal lines on that graph must be some rather impressive gravity wells from the point of view of passengers, though I could be wrong. He talks about a desire to do numerical simulations and to even do *real experiments* looking for such solitons… that sounds like fun to watch!
Using such a system would seem able to create paradoxes, but is there some “local rest” frame at each point in space that the machine can’t move backward relative to? Are these paradoxes any more disruptive than the daily mishaps of rogue precognitives? Is “dark matter” and/or “dark energy” a vast swarm of alien spacecraft from before the beginning of time multiply occupying every point in the universe and flashing through us at every moment? Find out in next week’s exciting new installment! :)
My favorite science explainer has a lucid explanation of complex science such as warp drives and FTL travel:
https://www.youtube.com/watch?v=8VWLjhJBCp0
Regarding causality violations from FTL travel;
https://www.youtube.com/watch?v=-2c0P2CEU9A
Her sense of humor is dry, her wit is sharp, she challenges science orthodoxy (many particle physicists are not happy with her observations regarding the ongoing failures of their pet theories) and she make entertaining music videos as well.
It’s a good short explanation, but I don’t think her notion of a reversed arrow of time is really right. The way she sees it, the person making a trip that lands back in the past will get getting younger at the end of the trip because they are going into the past. But … with FTL travel, when the person is going back in time is a matter of opinion! So at what point does time just stop going forward, and a second history of the person rewinding in time is spliced to meet up with it?
I think the actual solution is a very limited reversal of time. Entropy continues to increase aboard the spacecraft, and no eggs are unscrambled. Yet when it arrives, it is in the past, and it *cannot* conflict with any other valid observations of the past. The result is that probability is being messed with – not all the range of possibilities are possible – but the effect of this is very subtle. It is also comparable to a typical precognition story from the present day: a person remembers he is about to see an accident, and infuriated by this, pulls off and walks into the woods, where he scares off a deer that runs into the road and causes the accident. Time is *partially* reversed, in the sense that *some* outcomes are unavoidable.
Is there a causality violation at the quantum level? Quantum Mischief Rewrites the Laws of Cause and Effect.
As for seemingly strange things at the quantum level, what about this evidence that the imaginary number i ( SQRT(-1) ) is really part of the quantum world and not just a mathematical shortcut? Imaginary Numbers May Be Essential for Describing Reality.
Sometimes I can believe 6 impossible things before breakfast, including FTL travel. If FTL travel exists, and it is relatively cheap, it would have relevance for the Fermi Question.
“The Universe is not only queerer than we suppose, but queerer than we can suppose.” -J.B.S. Haldane
A linear view of causality is conducive to efforts at control, and susceptible to apparent disruption. Alternate views including the complexity of networks are less affected.
Not surprisingly, Sabine has a video on the “reality” of complex numbers and their relevance to quantum mechanics with reference to the cited paper.
https://www.youtube.com/watch?v=ALc8CBYOfkw
I’m not trying to promote her YouTube channel. It’s just that she is a respected scientist who does not fit the stereotypes and offers explanations that are not designed to grab headlines (thinking about Michio Kaku and Neil deGrasse Tyson).
I have now watched a few of her videos based on your links. She is very good at explaining ideas. So good, that I subscribed to her video channel.
I guess those folks with a jaundiced view might be forgiven their cynicism. As Yogi Berra had astutely noted, “In theory there is no difference between theory and practice. In practice there is.” Pursuing similar lines of thought, one may assert that there is only one electron in the entire universe.
Time will tell, but in whose time is yet a wild guess.
The easier it is for FTL travel or communication to be implemented, the harder it is to explain away the Fermi Paradox. If superluminal starships or radios can be easily constructed,, the best way to explain why we haven’t been visited yet is to accept that technical extraterrestrial civilizations are exceedingly rare.
A galaxy where numerous species had the ability to easily communicate or visit one another would be essentially one culture, either united by mutual interests or long destroyed by competitive conflict.
Civilization needs a wilderness. Like microbial cultures in a Petri dish, quick growth would quickly lead to crowding.
It’s sounding like an infinite improbability drive
Why muck about tediously in hyperspace…
If only. I just need a Bambleweeny 57 and an atomic vector plotter to attach to my “Earl Grey, hot” tea at breakfast.
Solitons are solitary waves. I don’t think that solitons effect the energy level of a artificially or human made space warp. To effect the energy of the field, we have to change the amplitude and the wavelength which is also true of quantum field theory. Any changes in the strength of the warped field from solitons of the warped field probably would only minor, an intuitive educated guess of mine.
Dr. Harold White and Dr. Eric W. Davis have already thought of an idea to reduce the energy requirements of negative energy by pulsing the negative energy field like a directed energy weapon or laser. I assume the negative energy waves would be high energy, short wavelength, which would make the spacecraft go fast, or we could use only low energy, long wavelengths without any pulsing which would reduce the intensity of the field and make the spacecraft go slow. Consequently, the enormous amount of energy needed to make negative energy as explained in this article is out of date. I think the energy needed was negative 722 kg. https://www.youtube.com/watch?v=OGYmowtelzA
What we have described above is manipulating the energy field but not how we could make an repulsive anti gravity field or even a gravitational field which we do not know how to do. General relativity is what determines the geometry of space or the lack of geometry so the type of wave is subordinate to the larger principles or GR which controls how space curves and moves.
from the paper :
“This paper addresses the first critique by constructing a new class of hyper-fast soliton solutions within general relativity that are sourced purely from positive energy densities, thus removing the need for exotic negative-energy-density sources. This is made possible through considering hyperbolic relations between components of the
space–time metric’s shift vector, which depart from the elliptic or linear relations that limited solitons in the previous literature to require negative energies.
Further, the stress-energy sourcing these solutions fits the form of a classical electronic plasma, placing superluminal phenomena into the purview of known physics.”
The problem with your idea Henry Cordova is that ET’s with FTL don’t have to communicate with us if they don’t want to. I recall seeing on a film on youtube Miguel Alcubierre saying that we can’t see a warp drive if it is moving faster than the speed of light. Swiss psychologist C. G Jung wrote the same thing in one of his letters. He said that anything that moves faster than light would be completely invisible.
I’ve always been totally mystified by the pronouncement that an object that is moving at FTL is somehow how “invisible”. In just simply thinking about this issue without any mathematics wouldn’t it be reasonable to assume that a FTL moving in some kind of fashion through the vacuum of space would happen to (at least in an instant) occupy a given position in which some photons would be right at that same space that would be occupied by the FTL ship? Doesn’t this seem the least bit reasonable to anybody? And if those photons are occupying the exact same space as the FTL at that instant then it would be reasonable to assume that some of them would be scattered in random directions which would be intercepted by somebody’s eyesight.
It’s certainly true that an object that is moving at FTL speeds would not be expected to be caught up by photons that are attempting to intercept it by catching up with it as it’s moving away from the source of the photons. Photons which would be moving toward the object would be expected to suffer some kind of reflection at various angles and bounce off toward some optical receiver of some type. Thus how can we talk about these things being invisible?
But the FTL ship is not moving through usual vacuum. It would be doing something like cutting the spacetime fabric in the front of the craft and sewing it back behind it, as seamlessly as possible. The particles on the fabric do not notice anything. There is another reason that the ship should be minimizing a disturbance to spacetime – if it actually interacted with any particles from outside, these are likely to have insanely dangerous kinetic energies relative to FTL ship.
Listen, if FTL doesn’t work out, there’s always wormholes…
https://interestingengineering.com/humans-could-survive-trip-through-wormhole
Okay, a one little bit different idea from my side when it comes to not use negative energy (it is quite different than Lentz’s paper also): so if we replace the negative energy density area with negative pressure (but possessing positive energy), like for example the inflaton field, wouldn’t it act in the same required manner ? This stuff would still make the trace of the energy stress tensor negative in total, or am I wrong ? I.e., in short, would the inflaton (which could in fact be actual stuff and can expand space time) make better choice instead of assuming something with negative energy for the model of a warp drive and create the required repulsive effect on space time …? Of course, if one presumes that the inflaton field can be reproduced locally and for short period of time, that is.
I guess this would count, heh ?
FTL makes the Fermi paradox worse; I suspect FTL is impossible thusly. In particular, the most fundamental constraint on expansion, the light-cage (which I suspect kills all Von Neumann-like civilizations very quickly), is broken by FTL.
http://www.physicsmatt.com/blog/2016/8/25/why-ftl-implies-time-travel
Also, FTL necessarily implies time travel, warp drive or no. It’s inherent in the nature of space-time. Causality may well be overrated.
Law,
I think you are correct in part. If FTL were possible, then REALLY: Where is everyone? But of course there are many places in the universe more interesting than Earth to visit!
So happy to be in the deep water with everyone.
From my limited exposure the fields of relativity – both kinds – and quantum are so mind boggling that most learned people who are interested in such matters have been able to grasp only a corner or two of God’s elastic arcre, whilst other corners will tend toward zero or infinity. If we each hold a corner where we have the best grip, others can do the same. Sort of a group mind collaboration.
An Alcubierre warp drive needs the expansion of space in order to work. I personally doubt you can make an expansion of space without negative energy, I have to question the idea of an anti gravity effect which uses positive energy density since all matter and energy with positive energy density that we observe in our universe makes a contractive gravitational field which is predicted by general relativity. As long as we can expand space, we can make a warp drive, but know one knows how to make the anti gravity effect which is thought to cause cosmic inflation.
We have some ideas. I think more money should be spent on making negative energy in the laboratory so we can figure out how to make warp drive and FTL. Around ten years ago, I talked to a couple of astrophysicists and they said it is probably not possible to use dark energy for space propulsion, the reason being dark energy comes from nothing or we don’t know how to make it. According GR, the expansion of space is very possible. There are dipole repellers in the local flow of galaxies in the local group not part of the Hubble flow which behave like anti gravity. I wonder it there is any negative energy in that repelling field. https://en.wikipedia.org/wiki/Dipole_repeller
Is is there negative energy in the empty space which expands between two black holes just before they collide? When the gravity waves detected in LIGO cause the tunnel to expand and contract, is that negative energy that causes their expansion? Can a gravitational wave go below zero into the negative energy if you squeeze it or change the amplitude?
I am not sure if a field of mostly gravity wave solitons would result in a more efficient space warp. I can make an intuitive guess that a strong, local gravitational field in a space warp might have a lot of soliton waves like near black holes. The reason being is high energy, short wavelength gravity waves also behave like particles. In quantum field theory, the more you mix a wave to localize it into a single rise and fall to locate the position of the particle, the more it acts like a particle when the wavelength become very short. The idea of the the graviton being non renormalizable and not being able to remove the infinities comes up here, but that might not matter. Consequently, the idea of solitons in strong gravitational fields might help us learn something about the physics of gravitational fields and their strength? It still does not show us how to make one.
What caused cosmic inflation is not entirely unknown, in fact most of the theoretical ground is pretty well studied (it remains to verify it by some indirect observation of cosmic microwave background radiation or by some type of LIGO experiment, and hence – determine the potential function of the field which drove inflation).
In short: there was a scalar field (called the inflaton), which has a certain potential. The field has the property to have large potential energy with constant density (absolutely the same as in cosmological constant/zero vacuum energy model but many orders of magnitude higher). Where comes the repulsive mechanism from ? It’s from the negative pressure. Energy density and pressure both take part in the Einstein’s stress tensor. Besides, in the Friedman equations for expanding universe, pressure is multiplied by 3 and energy density only by 1 if I remember correctly. So substance/field with rho = -P would still create repulsive effect. In fact, the difference between P/rho is exactly 2 units in favor of P after subtraction which accounts for the doubling of each space-time patch in each time interval. This is derived and outlined really well in the original paper from Alan Guth about inflation (also here https://ned.ipac.caltech.edu/level5/Guth/Guth3.html).
You can envision space time as a volume in an expanding cylinder during a thermodynamic process: E (energy) = -V.P . But V (volume) is always positive value. If you divide by V, then E/V = -P. E/v=rho – energy density and then obviously => rho = -P.
The exact mechanics how to produce false vacuum bubbles with inflaton field and make them inflate is described pretty well here:
https://arxiv.org/abs/0908.0283
Basically what one needs is a huge powerful particle accelerator to create small region with high enough energy density, equal to the inflation period in the Big bang. And then see it grow exponentially fast, expanding space-time.
Of course you can blow always the entire current visible universe (https://medium.com/starts-with-a-bang/how-to-destroy-the-entire-universe-5bd32cf6f985). So you have to be careful – one needs to recreate the energy density for a specific portion of the potential inflaton function – not too high to inflate uncontrollably, and not too low. You need maybe to make small “oscillating bubble” and just dump more energy with particle collisions periodically so that inflation ends earlier for the bubble, then begin to shrink due to gravitational collapse and then make it inflate again.
I envision this mechanism for warp propulsion. If some manages to engineer/design such distribution with “locally” inflating bubbles as a shell + the corresponding dense positive mass/energy, one could achieve the needed warp for propulsion.
But that’s just my idea.
Back to Lentz’s paper: maybe first it is needed to read the other work on the topic of positive energy warp drives by Andrey Bobrick:
https://arxiv.org/abs/2102.06824
It describes a shell of very dense matter/energy, which basically makes it act as shell black hole, i.e. space time is distorted locally in shell/bubble manner around the craft which still stands still locally in the middle and it is shielded by the other flat space time in the universe.
But as the authors outline this space warp doesn’t move faster than light, in fact it needs first some sort of outside acceleration to sub C-speed and then it continues to fair freely with the same velocity in space. Ironically the authors comment Erik Lentz’s paper in their work and go quite sceptical about his derivations, insisting that FTL bubble is not possible in reallity.
Anyway, after reading Lentz’s work I interprete it crudely for my self in the following way: he, similar to Andrey Bobrick, uses high concentration of positive mass/energy, to make local (maybe ringlike?) distortion, but still positive curvature distortion, like around black hole for instance. The trick is that the energy distribuation’s gradient varies hyperborically and hence – the curvature radius changes also in this manner (maybe some sort of optimization to the shape function by his side). The second is that based on his description and schematics, I personally imagine that this positive energy density is distributed in multiple rings with variying diameter and density/curvature. Which means that the difference makes them locally to want to “fall” always towards each other forward, but they get again and again projected forward. And space-time gets dragged with the rings. So there is gradient but not between positive/negative energy, instead relative difference between two regions with positive energy density and curvature but different value of those. And space is allowed to “flow” faster then light which is the key part. This phenomenon exists during frame dragging around rotating black holes: accretion material rotates sub light but space containing it moves faster than C. Space also “falls” faster than C in regular Schwarzchild blackholes, this is the reason why nothing , even light, cannot escape the event horizon. Same for inflation and dark energy expansion: on cosmic space is expanding faster than C.
And this flowing lump of space-time with local hyperbolicaly varying curvature radius that preserves it’s form is his analogue to the soliton wave in fluid dynamics, optics etc. Soliton but build from space-time.
So, I don’t honestly know if Lentz intended it to work in this manner but at least this is my common sense interpretation and I would engineer it in similar manner if someone gave me such task.
I think that he only outlines only theoretically possible mechanism for FTL and shows that it is not forbidden as a method, but practically I believe that FTL warp drives are impossible because of causality violations, they will probably become super unstable and collapse during FTL, and also possibly form event horizons for the ship.
But anyway, even sub light warp drive, regardless if it’s created in any of the 3 outlined methods (inflation, Bobrick’s way or Lentz’s), are really cool and give rise to a lot of benefits for space travel.
I don’t get it.
The soliton is localised.
The surrounding expanse of spacetime is not affected by the soliton.
The soliton may alter the passage of time experienced by the astronauts within it, but it can’t reshape the great expanse of spacetime through which its journey runs. E.g. clocks at the source and destination stars won’t change their synchronies just because a little soliton exists somewhere.
Therefore, the usual rules of SR apply. For example, the rule that you travel backwards in time and violate causality if you move faster than “c”.
This concept seems like travelling the world on a railway car: the floor of the car is perfectly flat at all times, but that doesn’t mean the Earth is not round.
Am I missing something?
The admitedly crude concept I’ve assimilated is that the space immediately in front of the bubble/wave is condensed (and expanded immediately behind) as seen from the bubbles instantaneous frame-of-reference. So whilst the great expanse of spacetime through which its journey runs is largely unchanged, the bubble/wave transiting that expanse always sees the next metre in the journey much shorter than otherwise.
Similarly crude in concept, the gravitational wave is a sort of logitudinal wave (like a sound wave) that alternately compresses and expands spacetime as it propagates. If negative engergy is responsible for the expansion phase, then it must have been present at the source (colliding blackholes), or perhaps no negative energy was necessary to generate the gravitational wave at all.
Sorry but you’re missing my point.
Spacetime retains its shape outside the soliton. Therefore the usual rules of SR apply to any path you may draw through spacetime.
The spaceship does not leave spacetime – it is a “bubble” that remains embedded in spacetime. It therefore must travel slower than “c”. There simply ARE no superluminal routes through spacetime that it could follow.
I’m certainly not sure I have this right – but in the spirit of brain storming consider the ‘bubble’ not to be sphere of exotic matter/energy (as some of the warp theories explain it) but rather
A) to be a region (warp or ripple) of high-curvature spacetime propagating along a path. The speed of propagation is the speed at which the warp is contracting space immediately ahead of it (and expanding the space immediately behind). If the speed at which space can contract or expand is not limited by c, then wouldn’t it be possible for that ripple to then propagate faster than c?
B) Then consider the ‘source’ of the ripple to be mass/energy distribution in a flat region inside the bubble where it is stationary with respect to the interior spacetime.
Wondering where you see the greater difficulty, in A) or B) or both?
>> ” If the speed at which space can contract or expand is not limited by c”
But that’s my point. The universe is not made of a “space” that we could move through at arbitrary speeds.
The universe is made of “spacetime” and by its very shape it limits all speeds to “c”. It’s rather like taking a long walk on Earth – the furthest you can get is 12.7 Megameters, the other side of Earth.
You may imagine that it’s possible to just keep walking and go as far as you like – if you ignore the shape of Earth.
I partially appreciate what you are saying, in that a craft propagating through a ‘condensed’ space would also experience slower time, offsetting any advantage speed. There seems to be something in the idea that the craft itself does not propagate through that spacetime, being encapsulted in the bubble. I don’t understand that, nor do I understand inflation theory, but the inflation theory posited that the spacetime of the early universe expanded faster than the speed of light in a fraction of a second. I think the warp is an attempt to somehow exploit that effect.
Yes, it’s true that spacetime can expand such that objects move apart faster than “c”.
But, that process involves reshaping the universe. You can’t achieve the same effect by making a bubble of locally distorted spacetime.
@David Byrden,
“But that’s my point. The universe is not made of a “space” that we could move through at arbitrary speeds.
The universe is made of “spacetime” and by its very shape it limits all speeds to “c”. ”
ahh … I think I’m beginning to see the source of your difficulty. You are somehow wedded to the notion that it is the nature of ‘space time’ that is the limiting factor to universal speed limit. I’m not sure where you got that idea, but the fact of the matter is that the nature of the limit of “c” is not because of the existence of space-time in and of itself, but more seemingly lies in the nature of being unknown.
I know that’s not a satisfying answer but the truth of the matter is there’s no actual stated reason as to why material objects in normal space (i.e. read here the word “space-time” for the words normal space) cannot be pushed beyond the given limit of “c”. At this juncture in human knowledge we just simply don’t know the reason why the velocity of light (and the universe at large) does not permit objects to be pushed beyond that limit.
In Einstein’s original 1905 paper it is pointed out that the Lorentz factor is built into the equations and the Lorentz factor in its embodied form results ultimately in the speed of light being the ultimate speed limit. That all being said, this new person’s paper from Germany is not talking about the velocity of an object in normal space, but is talking about the idea of space-time itself representing a elastic medium which can be manipulated and controlled in such a manner as to propel a spaceship that is embedded in a portion of that space time. So if you can divorce yourself from the idea that the shape of “space-time” is somehow limiting for an object to move at any arbitrary velocity you will have achieved what is actually being presented here. That’s the best I can explain it.
You insist that “c” depends on something else, something unknown. The “curvature of spacetime”, you say, is not the real reason for “c”. Perhaps spacetime is not curved at all, and the Lorentz equation is merely a convenient way of describing what happens?
Well, perhaps. But it’s what happens.
The universe does *behave* as though spacetime has a shape that limits all speeds to “c”. It behaves like a Minkowski space R1,3 (if I have the notation correct). Who cares if it’s an illusion? There it is, and we can’t make it disappear.
Now, the proposal is to break this law in a small bubble, large enough to hold a spaceship. But the great expanse of spacetime that it journeys through, will retain its shape. You will merely be “surfing” through it on a tiny “wave” of your own creation. Perhaps the flow of time for your astronauts will be under your control, but the spacetime distance between source and destination will not change.
And for that reason, you won’t be able to escape effects such as relativity of simultaneity, length dilation (of the journey itself), time dilation and so on. I don’t care how much time your astronauts experience while in the ship – I know what time it will be, on Proxima Centauri, when they step OUT of the ship.
I am saying that it’s valid to apply the Lorentz equations to this proposed FTL journey, regardless of what may happen within the spaceship. And that equation tells us that we can make a round trip, arriving back on Earth before we leave. A causality violation is the consequence of FTL travel.
As Einstein pointed out.
“I don’t get it.
The soliton is localized.”
I looked through the paper and while I have no exposure really at all to general relativity and all the manifestations of its mathematics I was able to kind of get a (albeit crude) perception of what he was attempting to do. I can see that you would be confused by the idea of a soliton being enable to have the characteristics of an expansive ‘warp bubble’ and allowing that expansive/contracting bubble be capable of driving the craft.
How can something which is compact be able to expand/contract if it is highly localized which is what a soliton is defined as? I think the answer to the question is that the positive energy is what is localized (the soliton) and that localization permits the space time to undergo the contraction/expansion necessary to drive the ship. At least that’s my take on the matter.
No, that’s not what confuses me.
Maybe this is a silly question, but … suppose you can actually use this as a warp drive – put together the field, expand space behind and compress it in front, stop at the destination. In the process, you move along a short timelike interval from point A to point B rather than the spacelike route you would usually have to take (if you could). Does that mean, by definition, that the operation of the warp drive created a wormhole? Is the pattern of red and blue tiles like some kind of manifold describing the throat of the wormhole? Are the places where space is expanded and contracted event horizons? Is there more than one way to conceptualize this math?
“The energy required for this drive travelling at light speed encompassing a spacecraft of 100 meters in radius is on the order of hundreds of times of the mass of the planet Jupiter. ”
Isn’t this kind of inherent? You’re deliberately distorting space-time. The only force we know of that can do that is gravity, and the only source of gravity we know of is mass.
The distortion of space-time has to be fairly extreme, this implies a high mass density.
Prediction: The only way to produce any sort of space warp without astronomical mass densities, is if you can somehow break the equivalence between gravitational and inertial mass, create gravity not in direct proportion to mass.
I don’t think we’ll be able to do that unless we can stop being confined to “local” physics, the special case dominating the universe we live in, and start working with “general” physics of the sort string theory implies exists, perhaps off the brane our universe exists in.
Maybe something we’ll eventually learn to do, but for now I’d rather concentrate on conventional physics space drives. Maybe we’ll get lucky and find some quark droplets out in the asteroid belt, but we can always just brute force our way into being a K-2 civilization, build a statite array around the Sun, and do interstellar travel by beam propulsion on a large scale.
From what I recall reading about warp drives, there is no causality violated in them because one is dragging one’s local space reference frame with the ship, so that there is an event horizon in the warp bubble and one is trapped in side it so there is a casual disconnection, but only locally. Time remains the same inside the ship as on the outside. It’s not the same as a worm hole as far as distance is concerned, the expansion and contraction cancel each other out so there is no change in distance so it’s not the same as a worm hole.
I’ve done some thought experiments on what does happen and using special and general relativity with a warp drive and there is a very interesting effect. I saw on youtube a physicist who said the space is wrapped or pulled around the warp drive bubble faster than the speed of light. If that is true, then an event horizon would form so no light could not get outside the bubble from the ship because the faster than light space being wrapped around the spacecraft would completely block it. It would be completely invisible at faster than light speeds. Furthermore, an observer, if it was possible to observe the warp drive at relativistic speeds which is probably not possible due to SR and GR, the warp drive would appear to be length contracted as it approached the speed of light and it would get smaller and smaller once it reached light speed or faster when it would disappear completely from our local space universe; it would be outside of our universe in hyperspace. A spacecraft with Alcubierre warp drive at FTL could pass right above our solar system and we would never know. No one could detect it, not even the ET’s in local space who made it, so the FTL spacecraft appears to be smaller than the plank length from local space. This would also solve the space debris problem with a natural deflector shield made from the faster than light space passing around the ship or one becomes so small as observed from local space, one goes right through things or takes a shortcut around them through hyperspace.
>> “Time remains the same inside the ship as on the outside”
But there’s no such thing as a default “time on the outside”.
The flow of time depends on your chosen reference frame. That’s basic SR.
If we can’t do FTL or wormholes, there is always Orion…
https://toughsf.blogspot.com/2021/01/moto-orion-mechanized-nuclear-pulse.html
Or we can fake it. An Orion ship launched in the Kennedy era.
Ascension
Or the whole Universe is a simulation. You would think that might make things easier. Just ask the Programmers to tweak the code.
I like Brett’s suggestion that constants can be different in different parts of space, with modifications being made by advanced civilizations. Tricky, no doubt with unintended consequences, but conceptually interesting. If c could be increased by several orders of magnitude, that might make interstellar travel a lot easier.
But “c” isn’t like the temperature – it’s a measure of the curvature of spacetime.
Changing the speed of light in some area is not like raising the temperature of a region on Earth. It’s more like reshaping Earth to be less round.
The speed of light is indeed intrinsic to our particular universe. However:
1. I invoke Clarke’s 3rd law
2. We really have no conception of what advanced ETI technology is capable of.
So, to make a point that is applicable to the next post on technosignature detection, we should consider possibly outlandish ideas.
The anthropocentric view of the universe is that we are in a multiverse, where the constants are Kipling-like “just so” to allow us (and other life) to emerge. Unless a theory explains how our universe creates the needed properties, then randomly creating bubble universes to brute force find the working ones on a cosmic supercomputer is the only mechanism. So what if ETI creates a universe that works with c at a very different velocity, but also works? What if that universe is not closed off, but contained in a bubble inside our universe that can be entered and exited at will?
Now imagine that bubble enclosing a volume of space that allows life to exist and that ETI can populate it, maintaining a globular-sized, or even galaxy-sized volume to live in. What if we could detect that bubble by the timing anomalies of light from some event passing both past and through that bubble? (e.g. An apparent occultation or reverse occultation of a supernova moving against the bubble).
I don’t expect this is possible, but we should open our minds to possibilities rather than only considering what our current science and technology allow.
As Haldane said: “The universe is not only stranger than we imagine; it is stranger than we can imagine.” So let us at least stretch our imaginations rather than limiting them.
Somebody once said “I try to have an open mind, but I don’t open it so much that my brain falls out”.
I didn’t raise my objection here due to a “limited imagination”. I am not simply kicking back and saying “New idea? Nope!”
I’m pointing out a difficulty that I think is valid and makes the whole thing impossible – the shape of spacetime itself. The proposed soliton distorts spacetime but only at a very local level. How is that supposed to change the spacetime distance between origin and destination?
Direct Fusion Drives Could Send Us Flying Across Space in the Blink of an Eye [I am just posting what they put for a title, don’t blame me.]
Technology may get us across vast stretches of space in near future.
By Jaime Trosper
Mar 15, 2021
https://interestingengineering.com/direct-fusion-drives-flying-across-space-blink-of-an-eye
That article isn’t relevant to this topic at all.
They are proposing a practical type of engine that may be possible to construct. Their proposed speeds are nowhere near “c”.
Heh, they start by talking about breaking the lightspeed barrier and leave us with hopes of Titan in two years with D-T fusion. I feel baited and switched.
Quote by David Byrden: >> “Time remains the same inside the ship as on the outside”
But there’s no such thing as a default “time on the outside”. Then you wouldn’t need a cell phone or a watch. Space and time governs all reference frames so that time is something that is independent of our conscious perception of it. SR does not exist without GR. Think about radioactive decay as a clock. It would be nice if we could choose a reference frame where SR and GR don’t work or apply, but there isn’t one including inside black holes where time is postulated to stop or does it really only move very slowly. Either way GR still works inside of black holes. According SR and GR there is no physical reference frame which is outside of time.
As far as SR is concerned a good example is light Time stops for for a photon moving at the speed of light, but time only stops for the photon but not for the universe that contains it so it still takes billions of years for a photon of light to cross the universe. Space can move faster than light because locally there is very little energy in it only virtual particles of the quantum vacuum zero point energy.
I think we both agree that there is no outside of time, but there is an outside of the warped space bubble of an Alcubierre warp drive which forms an event horizon which is inaccessible to anyone from outside and while at FTL one can’t leave the local space reference frame because of the extreme curvature of warped space would be destructive to anyone who ran into it.
Quote by David Byrden: >> “Time remains the same inside the ship as on the outside”
I didn’t write that.
I was quoting Geoffrey Hillend.
Hence the quotation marks.
Most interesting. Can’t wait until we start “bending metal”, and build some hardware, to test this idea.
We may have already done so, at least in Sci-Fi movies. Contact had a very interesting concept in the spherical capsule that encases the traveler, with a dodecahedron surrounding the sphere which was dropped into three rapidly spinning gimbaled rings. Remember the chair that was attached to the capsule by the engineers, but was not in the plans sent by alien civilization. Well, it was vibrating so violently that it broke free from the capsule and then everything was fine.
Think about it. ;-}
Research Group Proposes Way to Travel Faster than Speed of Light.
https://learningenglish.voanews.com/a/research-group-proposes-way-to-travel-faster-than-speed-of-light/5815680.html
VOA no less, seems odd, but quotes Lentz saying in 10 years may have working unit. No mention of this in the YouTube presentation last night Philippine time, but it is still up for those who want to watch.
https://centauri-dreams.org/2021/03/11/ftl-thoughts-on-a-new-paper-by-erik-lentz/#comments
Main part about an 1 hour and 10 minutes long.
Correction for the link:
https://www.youtube.com/watch?v=6O8ji46VBK0
I was severed from the internet for a day+ and I’m almost caught up after being forced to deal with the real world. Reflecting on the topic and some of the comments I think a review of a few basics may be helpful to some. Those who know more than I do should feel free to address any errors I make.
That deception “FTL” term seems to confuse many, as does “spacetime” vs space and time. Let’s look at conventional physics, the stuff that we know works. You have a powerful spaceship. There is no theoretical constraint on how quickly you reach your destination. Want to cross the galaxy in a year (month, day?)? Go for it. Ordinary relativistic physics is on your side.
The practical difficulties are legion. Perhaps the energy budget is the most severe: it takes an enormous amount of energy to accelerate to and decelerate from a high relativistic velocity. Regulars can list the many other practical problems so I’ll skip over those.
Assuming these problems are solved (ha!) there is a complication: you can never go how again. You have spent a year or two, by your time, gallivanting around the galaxy. Not so back on Earth. Millions of year may have passed. Most sci-fi writers of space operas happily sweep this under the rug. We have to deal with it in the real world.
Due to the practical difficulties and the impossibility of making it back home in time for dinner there is an interest in alternatives. Hence Alcubierre and similar physics-bending exercises. I say bend rather than break since these concepts sit precariously at the bleeding edge of theory without quite falling off the cliff. Maybe.
Putting aside Lentz for the moment and considering the better studied Alcubierre concepts, there are a few things to be said. First, the Alcubierre warp drive in its various iterations is no more FTL than the conventional relativistic travel. You are still traveling on a time-like curve. So, no time travel or other crazy stuff going on.
The problems involve the energy conditions. As it stands the energy requirements, and their exotic form and construction, are no better and may be far worse than conventional relativistic travel. I have nothing to say about whether these difficulties can be overcome or are possible. Alcubierre warp drives are only useful if the energy problems can be overcome. And you still won’t make it home in time for dinner, unless your dinner date is far in the future.
Assuming Lentz is on to something with gravitational solitons (although I strongly doubt it) you may be no better off than conventional and Alcubierre drives. The energy problem and the construction problem remain. Again, forget about making that dinner date.
For brief travel time (from the perspective of the traveler), tractable energy budget and to get home in time for dinner requires something exceptional. Certainly causality is a problem, no matter the mechanism, though whether that’s a show stopper is uncertain. Since whatever the mechanism it will have to connect spacetime points, the origin and destination, with a non-time like curve. That’s unavoidable, even if the proximate travel method is not strictly FTL (space-like curve).
One popular possibility is a wormhole. It is at least theoretically within the realm of possibility. If possible the energy conditions appear to be formidable. Whether our spacetime allows for these non-simple connections is unknown. The universe may not support construction of these connections.
Perhaps there’s a solution lurking out there that we may one day discover. However there are many other difficulties with wormholes that I will skip over. This “comment” is already far too long.
“Assuming these problems are solved (ha!) there is a complication: you can never go how again. You have spent a year or two, by your time, gallivanting around the galaxy. Not so back on Earth. Millions of year may have passed.”
I’m afraid that you have totally and completely missed the point of this man’s paper as well as the general conceptions of relativity in totality. The man (Lentz) as well as Alcubierre states explicitly that the internal structure of the bubble is flat space time; additionally the outside of the bubble (the universe) is also considered to be flat space time. In both localities neither portions of the space time are suffering any type of time dilation whatsoever.
In other words if you go to Alpha Centauri in four hours, by your watch that you have inside the bubble, and you turn around and come back home immediately in four hours you will have found that only eight hours of time actually passed by on earth. The clocks that are within the bubble are synchronized to the clocks that you have back home on earth-relativity does not apply in these situations. You have misconstrued, I’m afraid, will what relativity says with regards to what particular circumstances that you find yourself in at that particular point. You must address the paper to see what is being talked about. This is not time dilation as you have led yourself to believe.
The drive as originally described by Alcubierre does indeed purport to behave as you describe. That was 30 years ago and much work has be done since. There is a broad consensus that the Alcubierre drive cannot travel FTL, but there remains a small possibility that it can work sub-FTL. Maybe. If you have lots of exotic matter to play with. Conventional relativistic velocities require less energy, and still terribly difficult regardless.
The only variation on the FTL theme I’ve seen for Alcubierre is operationally no different from a wormhole. Like a wormhole the “path” must be constructed beforehand and traversed in an exotic spacetime bubble of some form or other. I addressed wormholes above so I said nothing about this version.
Why do you assume I did not read Lentz’s paper? I did, twice. Although most of it is over my head I did not see anything to give me confidence that it is more plausible than the Alcubierre drive. Of course I could be wrong. The FTL attributes it claims run into the same difficulties as Alcubierre’s spacetime warp and will likely suffer the same fate. So that is why I described it as I did.
I stand by what I wrote.
An Alcubierre warp drive does not have a reaction mass. It uses a space warp so the sum of inertial and gravitation masses is zero giving it a free fall geodesic which means the occupants inside the warp bubble don’t feel any inertial effects so there is no energy needed for acceleration and deceleration according to Newtons laws. The reason being one is dragging ones local space reference frame with one which is not affected by SR. The space itself is being pulled faster than light around the warp bubble. SR states that anything material can’t read the speed of light because it have to become infinitely massive and an infinite amount of amount of energy to get it there. One can still get close like the protons in the LCH. Spaceships might not fare to well at that speed. There is no inertial drag with a warp drive. https://en.wikipedia.org/wiki/Alcubierre_drive
What’s your point? I know all that, as do those I’ve been discussing this with, and we’ve gone well beyond your elementary description.
My point is the physics of the Alcubierre warp drive is not the problem since it is supported completely by general relativity. It’s the amount of positive energy density needed to make negative energy. When we make negative energy, there always needs to be a little more positive energy density than negative energy due to the quantum inequality law. The idea that there is a consensus of opinion of the warp drive can’t reach the speed of light is not based on SR and GR which have long been proven to work and are known as first principles.. I am not interested in challenging SR and GR, but only the idea that it takes too much positive and negative energy for a warp drive to go faster than the speed of light which is probably what the consensus of opinion is based on. I think it is completely wrong because those energy requirements are based on the extraction of negative energy from the quantum vacuum zero point energy of empty space, an assumption that is the only way to make it. I think we can challenge this assumption which is why I mentioned dipole repellers of galaxies, etc. It takes an enormous amount of positive energy just to get a little bit of negative energy from empty space like the Hawking radiation near the event horizon of black holes. What if that was the most inefficient way to make negative energy? I think it is. I think we can make gravity waves and anti gravity waves from the conversion of one or all of the other three forces and control them with much less energy than was previously thought without vacuum energy extraction. If this is true, then we could make a warp drive with less than the energy in one tea spoon of matter which is a lot less than 722 kilograms. I don’t wish to go into the details of this as I am writing my own paper on it.
Also I challenge the idea that we can observe something faster than light in a non inertial frame. Anything moving faster than light cannot be seen in any frame inertial or non inertial according to SR and GR which are frame independent. We can draw it on paper so something is outside like light cone, but that is only an abstract drawing on paper and not physical reality or space itself. If you try to observe that in physical reality you won’t be able to which is why I said that a warp drive in FTL outside the light cone is completely unobservable and invisible.
I’m sorry, but…. NO.
I understand that the short travel time experienced by the astronauts is “not Time Dilation”. But your description of how this would play out, contradicts the basic rules of SR.
This sentence shows the misconception:
” the outside of the bubble is also considered to be flat space time”
The problem is this: it’s NOT flat spacetime outside the bubble. It’s the normal spacetime that we live in. You can’t distort the whole universe, nor even just the few light-years that the ship will pass through. You can only enclose the ship in a tiny bubble. Let me put it this way: when people experience “zero G” in a NASA airplane, Earth’s gravity doesn’t actually switch off.
So, the rules of Special Relativity – which are a description of the shape of spacetime – DO apply. And they include the following:
1. If you move FTL in reference frame A, then I can choose a reference frame B wherein you are moving backwards in Time, arriving before you depart.
2. No reference frame is special. B is just as valid as A.
From which it’s obvious that we can set up a round-trip where you arrive back HOME before you leave.
I never said that a free fall of a spacecraft in orbit around the Earth removes the gravity. It is canceled out locally though so one does not feel any gravity. The same is true about the warp drive. I got this from a book called Cosmology by Harrison, p. 162, and 163, the idea that in a free fall the sum of the inertial and gravitational forces is zero which is why astronauts feel zero G. This is called the strong equivalence principle of general relativity. I didn’t make it up. Its not my idea. The rest of his argument was mass times gravity equals gravitational force, accelerate equals gravity, inertial mass time acceleration equals gravity. gravitational mass times gravity equals gravitational force. inertial mass equals gravitational mass. Warp drive has free fall geodesihttps://en.wikipedia.org/wiki/Alcubierre_drive
My point was that one does not feel any gravity or G forces which is what happens at relativistic speeds. At 77 percent light speed one pulls a constant one G. At 86 percent it’s two G’s. At 95 percent the G’s are a lot more. There is no inertial drag on the inside of the bubble because it is a reference frame at rest. Consequently, no energy is needed for acceleration and deceleration like rocket with a reaction mass in normal space under the influence of SR. With a reaction mass one adds energy to the rocket to push it forwards, but with a warp drive one changes the shape of space itself locally. There is no inertial drag on the bubble because it is space warp. The space itself around the ship moves faster than light. The ship is being both pulled and pushed like a conveyor belt at the airport which results in a freefall geodesic. Kaku.
If Erik Lentz’ idea is workable, we can travel back in time to the past. Causality will be violated. And that’s why I think the idea will NOT work.
Now, I owe you guys an explanation of that. So let’s take an example.
Imafine that it DOES work, like this : a rocket launches from Earth, then it creates the “soliton” and travels faster than light to a star, where it deflates the “soliton” and lands on a local planet.
You, my friend, are watching all this from your own ship. Let’s put you very very far away, equally distant from Earth and the star, so there’s no confusion from seeing nearby events sooner than distant ones, no Doppler effect, etc.
With the aid of a giant telescope you see the liftoff from Earth, then you see the “soliton” whizzing along faster than light, and finally you see the landing on the target planet. Everything seems OK. The humans have achieved something.
Now, let’s run it again, but THIS time your ship will be moving along at a good speed – not faster than light, but near it. Something that we KNOW is really possible.
And let’s have you moving in a specific direction; the direction from Earth to the star. But still you’re way off to the side, far from all the action, so you can watch it all play out.
What you see THIS time is amazing. At first, you see the humans preparing the rocket launch on Earth. Then – WHAM! – a flash of light appears near the TARGET planet. It’s the soliton deflating!. The rocket ship comes out of it, and makes a landing. The same rocket ship that is STILL ON EARTH.
And the soliton? It wasn’t there before the flash – but NOW you can see it. It came out of that flash and is moving TOWARDS EARTH very quickly.
Amazed, you watch the rocket crew on Earth prepping for launch, while you can see THE SAME PEOPLE unpacking their stuff on the target planet at the same time! They’re all moving in slow motion, because of time dilation, and they’re squashed because of length dilation, but you’re definitely seeing two copies of the same people.
Eventually the rocket launches from Earth, just as the soliton is arriving there. They meet up, and – WHAM! – they disappear into each other. Nothing is left.
What just happened?
What you’re seeing is called “relativity of simultaneity”. In plain terms, it means that there isn’t a single “now” moment shared by the whole universe. Events in distant places can happen at the same time for one observer, and at different times for other observers. It depends on the observer’s frame of reference – and ALL FRAMES ARE EQUALLY VALID so this is not an illusion or a trick.
You can see where I’m going with this, can’t you? If a “soliton” travels FTL in some frames of reference, then it travels backwards in time for other frames. And all frames are equally good.
So a crew can go to a planet, they can arrive BEFORE THEY DEPART in a given frame of reference, then they can create a second soliton to travel FTL in THAT frame which means it goes backwards in time for Earth’s frame…. so they will arrive back on Earth before they leave.
I have not read the Lentz paper but I know it doesn’t contain a solution to this causality violation – because the shape of spacetime itself makes this possible. You can’t prevent this by making a tiny distortion of spacetime around your rocket. You would have to reshape the universe.
“Amazed, you watch the rocket crew on Earth prepping for launch, while you can see THE SAME PEOPLE unpacking their stuff on the target planet at the same time! They’re all moving in slow motion, because of time dilation, and they’re squashed because of length dilation, but you’re definitely seeing two copies of the same people.”
” … you can see THE SAME PEOPLE unpacking their stuff on the target planet at the same time! ”
Therein lies part of your problem, you say you can see people unpacking their stuff at the same time… If you were moving toward the target planet the light from the target planet would reach you BEFORE the light from Earth reached you. It would NOT be at the same time but would be at different times for you; this tells you this is true just from the common sense idea of different informations being sent to you at different times on your own particular clock. From that you could infer the particular order at which events occurred and there would not be any contradiction.
You do realize from the particular ordering of the time events that the faster than light ship had already arrived at the target planet after you had received information from Earth regarding its departure. There’d be no contradiction in the activities.
>> “If you were moving toward the target planet the light from the target planet would reach you BEFORE the light from Earth reached you.”
No, that’s not the case, and I did explain why.
You, the observer, would be located far, far away from the whole journey : at many times the distance from Earth to the star.
And you would be located perpendicular to the journey’s direction. You’d see the whole journey laid out almost “flat” before you. The distance from you to Earth and to the destination star would be practically the same throughout.
Of course, with you being so far away, there would be a time delay in the light reaching you. You would see all these events long after they happened. But that delay would be practically *the same* for all points on the soliton’s journey. That’s why I speak of seeing things at “the same time”.
And, keen students will have noted, there would be a relativistic effect causing the Earth and star to appear somewhere forward of where they actually are. Plus, their light would be blue-shifted. I am assuming that, as a relativistic observer, you have optic software to correct for all this.
So I stand by my assertion. In your reference frame, and right before your eyes, you will see that ship arrive before it departs.
I don’t see that at all. As you say, from a great distance, viewing the ship traveling perpendicular to your line of sight, all the light will arrive from any point at the same time. Therefore if the ship arrived at the target planet instantaneously after it departed Earth, from your vantage point the light from both events would arrive simultaneously. As even FTL is not instantaneous, the light from the ship at arrival will reach you later than that from the departure. It isn’t clear to me that GR changes that.
However, I admit this is way beyond my understanding.
>> ” As even FTL is not instantaneous, the light from the ship at arrival will reach you later than that from the departure. ”
I’m going to explain this more clearly, for everyone’s benefit, because THIS is the fly in the ointment that makes the whole thing either impossible – or points the way to Time Travel.
You are correct in what you said. If every point of the astronaut’s journey is much the same distance from you (a far-off observer) then you will see the ship take off, travel FTL for a while, and arrive, in that order……
….IFF you are in the same Reference Frame.
But things get interesting if you’re in another reference frame. And you can still observe from much the same place as before, because a Reference Frame is motion, not position. However, you would have to allow for visual effects like blue-shifted light, and real physical effects like length dilation.
Here comes some math. Suppose we have a measuring system where the speed of light is One (e.g. years and light-years).
Suppose the Earth and the star are One unit apart.
Suppose your speed – relative to them – is “v”.
Suppose Earth and the star are in the same reference frame and their clocks are synced. Then each of them sees the other one’s clock as being 1 unit slow.
If you were in the same reference frame, you would see both clocks displaying the same time. That’s why I put you out there.
BUT….
you’re not in the same frame. Your relative speed is “v”. And let’s choose your direction: you are moving parallel to the spaceship’s path. The “earth to star” vector.
What will you see? You will see the star’s clock displaying a later time than the (synchronised) Earth clock. How much later? Exactly “v” units of time.
That, my friends, is what Einstein told us long ago.
Now, is it possible to see the ship arrive before it leaves? Yes, if “v” is greater than its travel time.
Let’s say the ship is moving at “f” in the Earth reference frame. Then it will arrive at the star (one unit of distance away) when the star clock shows 1/f.
So, you will see it arrive before it leaves, IF AND ONLY IF “v” is greater than “1/f”.
You’re obeying the laws of nature, so your maximum “v” is one.
Therefore we need “1/f” to be somewhat less than unity.
And that means “f” must be somewhat more than unity.
In other words : the Erik Lentz ship must travel faster than light.
And it does. That’s the whole premise.
In summary: if you travel FTL for reference frame A, then there exists another frame B where you arrive before you leave.
Good explanation. However, apart from energy issues of FTL, why is FTL “violating causality”? The perception of time travel seems to be just that, perception of light waves, not the physical ship. IOW, what we observe is no more time travel than movie special effects.
Now I understand that this is a reference frame issue and this means that different observers in different reference frames see different things happening, but what I cannot wrap my head around is that one observer sees nothing untoward, whilst another experiences a true causality violation at the macroscopic level. If you tell me “both can be true”, then I get caught up in an analogy to a “Schroedinger’s Cat” gedanken experiment.
The thing about “Reference frames” is this: yes, observers in different frames SEE different things happening, but more than that, different things ARE objectively happening. It’s not an optical illusion. As someone once pointed out, you can fit a long ladder inside a short garage by moving it relativistically fast.
So, how can we violate causality with an Erik Lentz soliton-wrapped spaceship? Let me give you an example with numbers.
Once again, let “c” be unity.
Assume that we have space-based “launchers” that can launch solitons at a speed of 5 relative to themselves (remember, all velocities are relative in SR).
Now, let’s pick a star that is one unit of distance away from Earth, and send a launcher from Earth out there at a speed of 0.7. That is less than the speed of light. Nothing funny is going on there. It will arrive 1.4 units of time later.
We have also built a launcher on Earth. At a prearranged time, we set Earth’s clock to zero and launch a soliton-wrapped spaceship from that launcher at a speed of 5 towards the star.
The timer on the star is synchronised with the timer on Earth. So, when the soliton-ship arrives there, the star’s timer reads 0.2. At the same moment, thanks to our careful planning, the launcher that we sent earlier also arrives at the star, still travelling at 0.7. And like anybody arriving anywhere, the crew adjust their watches to the star’s local time.
The soliton gets dissolved, the spaceship drops out of hyperspace and slows down to a speed of 0.7. It lands upon the launcher.
Now, everybody agrees that the local time is 0.2. But they don’t agree about the time on Earth.
Inhabitants of the star say that the time on Earth is also 0.2. But people on the launcher say that the Earth time is -0.5
And that’s true for them because of the reference frame they’re in.
Now, the launchers fires the ship back towards Earth at a speed of 5 (relative to the launcher).
I will describe the return journey in the launcher’s reference frame:
The distance to Earth is 0.7 (thanks to length dilation)
The time on Earth is -0.5 when we start.
The soliton-ship’s speed is 5.
Earth is moving away at 0.7 therefore the closing speed is 4.3.
The travel time is therefore 0.16
Earth’s clock has time dilation, therefore it advances by only 0.114 during the trip.
So the ship arrives home at the Earth time of -0.385
You will recall that the ship launched from Earth at time zero. So it has arrived home considerably before it left.
That is a causality violation.
@David Byrden , I don’t know if you in your presentation felt like someone was not agreeing with you or not, but I have to say that sums it up pretty well by saying that what you are seeing as a result of the FTL ship is in fact time travel or not.
I looked at a Wikipedia website called “Tachyonic antitelephone” in which there was an explanation for the phenomena of FTL and it’s impact on one-way communication. In the article that was given they address the issue of FTL and merely stated that in some reference frames the delta T can end up being negative. But they didn’t say that this was travel back in time.
So what is being perceived in no way invalidates a FTL ship which takes off and then arrives at the other place at a later time (as seen from Earth for example). I think that’s all anybody was saying was that it was what you been talking about: ‘relativity of simultaneity’, not invalidation of the principal. Here’s the Wikipedia entry below:
https://en.wikipedia.org/wiki/Tachyonic_antitelephone
What that reference tells me (as with others) that we cannot evade the time paradoxes even with hyperspace or wormholes. They are all going to result in time paradoxes. If this is correct, then any investigation into travel that is effectively FTL is futile.
As the article notes, one way to avoid this is with multiple worlds.
So you could travel FTL but then you would leave our universe and enter another one where a paradox is impossible.
@Alex Tolley,
I’m not at all certain why you feel that FTL results in FTL having associated with it a futility. The inclusion of the link simply indicated (in my mind) that, as you mentioned before, that there was no paradox here but simply the fact that there were lags/delays in which observation was received due to distance/time considerations.
This in no way invalidates the fact that there is an ordering in time in which a FTL takes off and then returns to his destination. Simple reasoning will tell you that an object (barring close time like curves in general relativity, which is what were not talking about) will have to come back to its destination AFTER it has left to go on a journey by the clock that is at the initial starting point. I think you would agree with that. So I wonder why you said that travel that is effectively FTL is futile ?
Finally, and lastly, all these particular FTL drives have had as a fundamental common characteristic within themselves of having a central region within the warp bubble as being flat in space time and therefore I would assume the clock in the internal region synchronized with the clock at its starting point would show a same passage of time as the clock that never left the starting point. Wouldn’t you agree?
The link you provided for the “anti-telephone” concerns causality violation – e.g. killing your own grandfather paradox. In the case of the anti-telephone, you could receive a phone call before you made it, perhaps telling you not to make teh phone call. You see the paradox.
Conventional issues with FTL usually r4evolve around the impossibility of going through the light barrier. Mathematically we can evade that using tachyons (which don’t exist), wormholes (extremely hard to hold open), and warp drive (Star Trek ships, or even Asimovian hyperspace ships).
The problem is that all these methods apparently result in causality violation, leading to paradoxes, which seems to be as inconceivable as breaking the law of conservation of energy.
So anything that creates a potential causality violation then becomes “impossible” and therefore would, a priori seem fruitless to pursue.
There were 2 get out possibilities in the link. Firstly that FTL doesn’t violate causality because you enter (or create) another universe that precludes the possibility of the violating causality. The second was that you would be prevented (in some undetermined way) to violate causality.
Given Everett’s multiple worlds hypothesis for some quantum effects, I could accept that that is a possible result of usings some FTL travel or communication. The universe preventing you from violating causality is not something I find palatable, it is like a really bad dream of not being able to reach your desired destination.
The really hard part for me however, is Byrden’s thought experiment that suggests that causality violation only happens in some reference frames, but not others. IOW, causality is, and isn’t, violated depending on the observer. Hence my use of Schroedinger’s Cat analogy. Experiments show the quantum world really is strange. It may be that this is also a feature of the macroscopic world.
I would like for some sort of hyperspace travel to be possible, like a stone skipping across water, entering and leaving our space in jumps. But apparently, causality violation makes that either impossible or has undesirable effects, like changing the universe. There would be no way to maintain a single interstellar culture if you tried to travel at effective FTL velocities, only if you travel at sublight ones.
But just suppose we could communicate at FTL speeds, that would imply that we might be receiving transmissions from our future. What an irony if we think we have received a communication from ETI only to find it was our future selves sending those messages.
Quote:
>> “Byrden’s thought experiment that suggests that causality violation only happens in some reference frames, but not others.”
Wow, I must be really bad at explaining things. Let me spell it out more clearly:
1. If you travel FTL in reference frame A, then I can find a reference frames such as B where you arrive AT THE DESTINATION before you leave.
That, in itself, is not a causality violation, because the two ends of the journey are far apart.
2. But now, if you travel BACK AGAIN and you do it FTL in the reference frame B, then you’re travelling backwards in time for the reference frame A.
The two journeys COMBINE to put you back on earth before you leave.
And no matter how you look at it, or transform the coordinates into other reference frames, it’s a causality violation.
@Alex Tolley,
First of all let me say that the link that I provided you to go to is not the be-all and end-all of the entire topic concerning FTL behaviors. I can only say this with any degree of certainty-and that is the fact that one must tease out very, very carefully any type of analysis on these particular frames of reference that are being used to justify the analysis. This is more than just transforming from one frame to another and then following the math and saying that we have showing proof of the argument.
What I can only say to you is that the only way to get any kind of feel whatsoever concerning this topic is to look at it through the prism of all possibilities and to look at it not only through math but through the process of pure logic.
For example the very first entry which was one way messaging which by the math indicated that in certain frames you could have a cause occur after the effect. When you look at the math with extreme care and apply logic to it, you would discover that an FTL signal with infinite velocity would never, ever under any conditions show time reversal no matter what the motion of one frame is with respect to another. If you spend the time you can verify that for yourself. So, just don’t simply look at an equation in a written paragraph and assume that the answer is cut and dried.
Finally and lastly, nothing that has been said so far invalidates FTL simply because of the fact that there is (presumed) paradoxes.
Quote:
>> “an object… will have to come back to its destination AFTER it has left to go on a journey by the clock that is at the initial starting point. ”
Simple reasoning based on what?
If we assume that SR is correct (and remember, it’s a very simple theory coming from the premise that no reference frame is special) then we get the following, which I explained in detail on this page:
“If you travel FTL in reference frame A, then there exists a reference frame B wherein you travel backwards in time”
This isn’t a local effect in your spaceship that you could remove by warping local space. No. This is a consequence of the overall shape of spacetime itself.
I spelt out an example where a ship can return to Earth before it leaves. I’m not saying that is impossible… I’m not saying it destroys Erik Lentz’ work… but I’m wondering why it doesn’t seem to be under discussion.
It was Einstein himself who pointed out in 1907 that you can use FTL for a causality violation. I’m just rewording what the great man said.
@David Byrden,
Quote:
>> “an object… will have to come back to its destination AFTER it has left to go on a journey by the clock that is at the initial starting point. ”
Simple reasoning based on what?
First off I would declare that if you abandon simple reasoning you will be led astray in your arguments. If I’m at a port of departure and an FTL ship leaves, and I have a steady clock with me as I wait for the FTL ship to return, then later (by my clock with me) the FTL ship appears then I would say that it has come back after it left. Now, granted if we are talking about certain types of general relativity solutions in which there has been presumably discovered close time like curves which have something to do with bending the space time in such a way as to return at an earlier time, then that is a different situation altogether and one could find one self with the ship arriving before it leaves.
However, if I’m sitting there at the port of departure, and my clock has not undergone any kind of velocity change to affect its timing than I would have to say that my situation holds.
Now I clearly understand that you have two frames which are called A and B, and A is some moving frame to observe something that is in FTL motion and you get an effect before the cause. Then you say you make a return journey to the starting point going FTL again and you have some moving frame (called B) which is observed by frame A and you see motion backward in time.
Now, I have not analyzed this in totality but there seemingly is something undergirding this analysis which doesn’t quite ring true. Now I confess I can’t quite put it into words but I believe it has something to do with the fact that to change from frame A to frame B-that is, how does frame A’ s coordinates transform to frame B’s coordinates involve some subtle (and unstated part played in the discussions) accelerations on the part of moving between the frames. And these accelerations are not being built into the arguments behind these movements back and forth between the frames. I have a feeling, that the analysis is not quite as thorough and complete as one would like to make a conclusion. There is an argument in Wikipedia on just this topic but that doesn’t prove anything simply because someone writes something there. Even if it does support your position.
In any event, it seems like an inertial frame in which one is on earth and one sees a departure and the person on earth does not move, it doesn’t seem possible that the FTL ship could in some fashion arrive before it leaves. That’s all I can say at this point, Einstein or not…
Does anyone have insight to share on what Lentz describes as the potential function, p( ), that he uses to derive his positive energy distribution. What does p represent physically?
“What does p represent physically?”
Good question: the symbol p that you mentioned, it’s called rho, represents energy (in this case positive energy) that’s needed by the system.
I wondered the same, however I did not spend the time to try and work through his derivations and conditions. It’s a sparsely worded paper with multiple references and I did not follow any of those external references.
The only thing I noted was his proposal of a plasma as an embodiment for the positive energy. It is mentioned several times in the paper.
The de Broglie–Bohm theory, also known as the pilot wave theory and the Heisenberg uncertainty principle are two very different interpretation of quantum mechanics. The pilot wave has solutions that fit better with solitons and phase locked cavities longitudinal wave generation in laser may be a way to generate Hyper-Fast Solitons at the quantum level. At that level energy requirements should be very low.
New analysis shows a way to self-propel subatomic particles.
https://phys.org/news/2015-01-analysis-self-propel-subatomic-particles.html
I know I’ve been condensing this subject but solitons have been deeply researched in optics, electrons and ions. The optical end has been mainly lasers and waveguides like fiber optics, electrons in particle accelerators and ions in the ion acoustic mode. The FTL concept that Dr. Lentz is working on may have early application as a way to send the StarShot Starchip to Proxima Centauri in a soliton in less then 4 years. What I am finding is a relation to early work by Moray B. King in his book on Tapping The Zero-Point Energy to the very similar material that is being researched in the last 5 years on solitons. There may be a relation to plasmoids, magnetic reconnection, solitons and bucking fields. Hyper-Fast Solitons, hyperspace and zero-point energy may actual be taking place in the magnetic reconnections on solar sunspots, we just need to look much closer in the area of magnetic reconnection plasmoids.
Once someone inside a Alcubierre warp drive moves faster than light, space from inside the bubble is completely black and starless because no light can escape the event horizon or no starlight get into the bubble from outside.
So that makes me wonder if such a device could go thru a star or planet in one piece?
@David Byrden, and others.
Back to the setup.
1. The FTL ship is hyperspatial to avoid issues association with travel in real space.
2. The ship leaves Earth and makes N skips to planet B.
3. The ship turns around and returns to Earth.
4. On Earth, the ship appears to return from planet B before it has left earth for planet B. Causality violation occurs.
Now what does a very distant observer perpendicular to the 2 planets see?
1. Outbound to B: The ships appears near simultaneously on Earth, all the reentry points at each skip point, and planet B.
2. Inbound to Earth: The ships appears near simultaneously on planet B, all the reentry points at each skip point, and Earth.
The small time delays between each skip mean that the return to Earth occurs after the ship has left. No apparent causality violation.
Granted that the distant observer cannot be on Earth, to experience the apparent time travel of the ship, but it appears that both situations arise:
1. Causality violation for an Earth observer.
2. No causality violation for a distant observer.
Now suppose the observer on Earth sends a message to the distant observer when the ship returns and when it leaves Earth.
The distant observer will receive a mesage about the return before the message about the ship leaving.
Now this seems to create a rather strange situation for teh distant observer.
Direct observation of the position and time of the flight appears quite normal. But reception of the messages sent from Earth indicate that the ship returned before it left. Indeed that message about the return arrives before the direct observation of the ship returning to Earth.
Now the observer has 2 different sources of information, one showing causality violation, the other not.
I am quite prepared to accept I have misunderstood the mechanisms described. To be consistent, one of the 2 observations is incorrect, most likely that of the distant observer observing the flight directly. So far I have been unable to understand the explanations that seem to result in the 2 disparate observations by the distant observer.
@David Byrden, @Alex Tolley, and others.
I hate to admit defeat to any problem; but at this point I just have to throw up my hands and say literally: “what the hell !”. This makes absolutely no sense, relativity or not. I finally read in a bit more detail in the area of the Tachyonic anti-telephone, and drilled down a bit further into what was being stated – and for the life of me I don’t get where (or how) you can send the message seemingly in one frame, transpose it into another frame for the return and end up with it possibly being sent before its received based upon the second frame’s velocity.
https://en.wikipedia.org/wiki/Tachyonic_antitelephone
It absolutely defies logic despite how the math (presumably) says what it says. This is obviously some kind of (Super Big Brain Problem) which is pretty far above my pay grade. I genuinely wish there would be somebody out there who would write in to here and go step by step, with concepts carefully defined such as to lay it all out in the exhausting detail. If you look at the Wikipedia article and look under the heading of a two way message and look at it closely, the explanation between going between reference systems is not exactly a model of clarity.
Furthermore, as this is an article (FTL: Thoughts on a New Paper by Erik Lentz) by this professor who obviously knows what he knows about relativity and all its ramifications it would seem incumbent upon himself to at least address the paradox for us in a bit of detail so as to assure us that in fact FTL travel will not result in unraveling of our no one physical universal ideas. As for you Alex I don’t know what to say about your explanation of jumping around in hyperspace. I’m afraid it’s muddy the water for me rather than adding any kind of clarity. I can’t say anything more at this point…
You didn’t specify the reference frame of the distant observer. Without that information it’s not possible to say what they will observe.
I’m wondering if you understand the Lorentz transform and the part that it plays here?
Anyway, I will try to answer you by assuming that Earth, the star and the distant observer are all in the same reference frame. And that the ship’s journey is the same one that I spelt out in an earlier post.
What the observer sees, was also spelt out by me in an earlier post. For the outbound journey, things look normal except that the ship’s speed is very high. For the return journey, it arrives before it departs, and the “skip points” are traversed in reverse order.
Note that I quoted times and distances, calculated on the principles of SR. If I am wrong, that’s where you will find my mistake. You can’t simply declare what the observer will see unless you do the math to back it up.
Well, if you believe Heisenberg uncertainty principle you do not know where you are at or what time it is…… ;-}
Don’t use that as an excuse if you are late for work. It only applies to the small scales like less than a millionth of a second.
My thought experiment tells me that the Alcubierre warp drive goes around things and not through them. Maybe one is only stretched thinner than a string in string theory at FTL speeds. In theory, it still is inside our universe, but one doesn’t have to worry about any space debris which makes the warp drive a very desirable, and the ultimate type of space travel. I don’t like the idea of going through things. Maybe it can’t and one would crash into them and die.
Another myth about the warp drive is that energy builds up in front of the spacecraft in FTL so when it comes out of warp, a huge amount of energy is released which irradiates the solar system one in visiting. It that were true, then the same high energy gamma radiation would irradiate the occupants of the warp driven spacecraft and kill them too. I don’t think that happens as space being rapped or pulled around the warp bubble one hundred times the speed of light would keep any energy from building up in front of the ship. Like a strong wind, the FTL space would instantly blow away any energy build up. Energy can’t build up there, so that idea is based a not very thorough thought experiment which includes the interaction of FTL space with the bubble.
Also the idea of not being able to steer the warp drive from inside the local space bubble due it it’s casual disconnection from the ship is removed if we don’t use the idea of some kind of solid, material negative matter which I think is ad hock, arbitrary and impossible based on known physical laws of how matter and energy with positive energy density hold together, but instead consider negative energy only an energy field like gravity, the reverse of gravity we can control it in an artificially made way without any matter. Such a space warp device could allow the pulsing of the ship for energy conservation and faster speeds and the steering of the ship from inside it with the simple pushing of a button.
Gravity control from its conversion from one of the other forces like electromagnetism or microwaves is not a new idea. It should not be too much of a stretch to consider we could do the same thing with negative energy. We would have to figure out how to make gravitons and anti gravitons which would make a field. These wave particles are the messengers of a field.
This comment is being directed at David Byrden with regards to your two frames moving at relative motions to one another. I keep returning to the page on Wikipedia concerning Tachyonic antitelephone and looking at the two way messages portion of the webpage and I’m continually bothered by the formulations and the conclusions that is being reached.
Your thesis is that a FTL ship leaves earth at some time T and later on returns from its destination to arrive at some later time call it T1 and because of some relative frame velocity difference you may have, the issue arises of T1 < T.
However I keep being bothered by the fact that the frame which the earth is in has not suffered any velocity change. To what frame are you referring to in which the returning FTL ship is moving backward in time? I just don't see it, I'm afraid. And if there is a frame whose velocity is such that the FTL ship appears to arrive earlier than it left, then how is that frame the same as the one which is the stationary earth frame in which everything has been witnessed to have occurred ? In other words the departure point has not undergone any change in velocity, has it not ?
There's something about the logic of FTL properties which seemingly shouldn't be tried to be fit into the framework of relativity, I keep being bothered by the attempts to adapt FTL properties to this particular subject. Perhaps that's not rationally scientific but I have a feeling that special relativity shouldn't be applied to an FTL situation.
Further commentary directed to David Byrden with regards to your two frames moving at relative motions to one another.
The more I considered the situation with regards to two co-moving frames, the more I began to suspect that the formulations (and conclusions) that have been stated here are not in any way correct. To address the situation I went back to Einstein’s original paper of 1905 in which he began his formulation of the relationships between time and spatial coordinates between two uniform moving coordinate systems. When I did so, I began to realize that Einstein formulated his equations based upon the conditions that first off, the uniform velocity of one frame moving with respect to the other would always have a velocity which would be less than that of light. That was done purposely. Secondly, the spatial coordinate which in his original paper was designated as x prime was in independent variable which had no dependents on time itself in the stationary system.
The understand anything which I am talking about you have to dig into his original equation and look closely at the variables that are involved in his formulation, and you will see that his entire equations that are derived from his initial summary of data’s are totally cast in the idea that other reference systems move with velocities less than out of light.
Now the equations which you have been talking about which purport to show that in certain reference systems (and involve FTL phenomena) which have some particular velocities will result in causality paradoxes which you say occur in actuality. As I just said Einstein’s equations are formulated specifically for any systems that move at velocities less than that of light; and light is the maximal velocity allowed. In Einstein’s equations when those velocities are allowed to exceed that of light you get nonsense answers coming out.
Similarly, if you take his equations and use them willy-nilly to allow yourself to insert FTL velocities within them, you will also obtain formulations and conclusions which give you exactly what you are talking about: causality violations. Einstein’s equations are meant for a very specific set of physical circumstances and cannot be applied universally. Given the fact that that FTL is a unique physical situation you cannot expect to apply Einstein’s equations to that particular system. I don’t know what the particular equations would be for the proper formulations to preserve non-causality violations, but I feel now pretty certain that Einstein’s equations of special relativity are not the ones you wish to use.
You seem to both agree and disagree with me.
We agree that Einstein’s SR equations (the Lorentz transform) isn’t intended to be used with any FTL speeds. If we presume that FTL exists, and apply the equations, we end up with crazy results, such as the causality violation that I spelt out in an earlier post.
What to make of it? One interpretation is to accept it and say yes, that’s what will happen if we build Erik Lentz’ proposed soliton. Time travel will happen. Who knows how it will play out?
Another interpretation is to say no, this is a Reductio Ad Absurdum, we have proven that FTL is not possible *because* it would enable causality violations. Any further work on the soliton proposal would be a waste of time.
But if I understand what you wrote, you make a third proposal. You say that the Lorentz equation should be discarded as unfit for this new purpose. A more comprehensive theory of relativity is needed, that describes FTL motion, and reduces to traditional SR theory when speeds are below “c”.
Well, that sounds like it should be true, but I am convinced that it is not. Why?
Because, as I see it, the Lorentz equation defines the shape of spacetime itself, just like the radius of Earth defines the overall shape and curvature of Earth.
I believe that whatever strange effects you can produce on your ship with a soliton or a warp field or whatever you call it, they remain *local* to the ship. The great expanse of spacetime that you pass through, retains its shape. And consequently, the rules of SR must still apply.
Let me put it this way: Adelaide, Australia, is upside down with respect to my current location. I can travel there in some fancy vehicle, I can choose a crazy route, I can immerse myself in magnetic fields in an isolation tank spinning around with a trained masseur inside, I can do all kinds of crazy things to myself on the journey – but when I get there and step out of my vehicle, I too will be upside down with respect to my current location. That’s because of the shape of Earth. I can’t mess with the shape of Earth.
“You seem to both agree and disagree with me.
We agree that Einstein’s SR equations (the Lorentz transform) isn’t intended to be used with any FTL speeds. If we presume that FTL exists, and apply the equations, we end up with crazy results, such as the causality violation that I spelt out in an earlier post.
Another interpretation is to say no, this is a Reductio Ad Absurdum, we have proven that FTL is not possible *because* it would enable causality violations. Any further work on the soliton proposal would be a waste of time.”
Yes as a matter fact, there is both agreement and disagreement here. As I said before if you look at Einstein’s original paper of 1905 you can see that incorporation of frames that move with velocities greater than light can result in negative times which could be interpreted as time reversals. As applied to his original equations you would fail to be able to synchronize clocks as is needed by his original formulation.
However, to declare that because there could be causality violations, and that in of itself, would of necessity declare the death of FTL transit that I continue to believe is not true and I have included here in a link relating the paper written by research scientist who are far above my pay grade who state that you can have FTL scenarios without time reversal. You can look at your leisure to see what you can make of it, personally for me I find it a difficult read but I’m not steeped in depth in relativity theory.
However I can say one thing which I believe is absolutely certain: if you have FTL signals which propagate with infinite velocity then you will have guaranteed no framework which you can devise which can cause time reversal. Just by definition all observers must be moving in forward light cones toward the future. Here’s the link to the paper that I promised you below:
https://arxiv.org/pdf/1407.2528.pdf
Charlie:
Don’t assume that a scientific paper is worth the paper it’s printed on. Einstein himself proved that FTL enables backwards time travel, so when these guys contradict him, we should check their math.
And I did. And it’s terrible.
Here’s the executive summary: they define “time travel” as returning to a point in spacetime that you visited before. That’s a useful and clear definition.
So you need make a return trip, a closed loop in spacetime, to Time Travel. They claim it’s impossible and they can prove it.
So they set up a simple 2-dimensional spacetime. Normal travel is going upwards, while FTL travel is going Right or Left. Your challenge, as I said, is to travel in a loop. They intend to prove that you can’t.
And THEN they say :
“we may assume, without loss of generality, that the future quadrant of … FTL observers is right”
They won’t ALLOW you to go left ! You can’t make a closed loop now ! The game is rigged !
How did that paper ever pass the peer review?
I feel like the discussion is among students discussing yesterday’s assignment while waiting for the professor to arrive to explain the answer.
1. Faster than Light (FTL) travel is any means to get from point A to point B in less time than it would take light to travel the same distance.
2. I use Asimovian hyperspace travel to avoid some other aspects of high fractional c travel – doppler effects, time dilation, length contraction, mass increases.
3. In Asimov’s version of hyperspace, a ship travels between 2 points in a very short period of time, i.e. near instantaneously.
We see something similar in the Star Trek movies where the ships quickly disappear in a flash of light and then appear at their destination as they drop out of warp drive.
4. At this time, hyperspace travel = magick.
5. Any travel where the time taken by synchronized clocks is less than the time light would take to travel the same distance = FTL travel/communication.
6. At any point in hyperspace travel, when the ship drops out of a hyperspace jump, the ship is at effective rest, and light is emitted at that point. Thus an observer from the departure point sees the ship disappear and appear later in accordance with the time that light takes to get back to the observer. An observer on the ship sees light from a time before they have left Earth as it has taken light the requisite time to reach them.
7. Where there is confusion is the different interpretations of the returning ship. From the ship’s crew, they leave Earth, reach a star in a very short time, and then return to Earth in another short period of time. They arrive shortly after they have left. (This is how Asimov writes his stories where hyperspace travel is involved).
An observer on Earth should see them leave, then shortly reappear, then a long time later see the ship appear at the star, as the light finally arrives back on Earth.
Other interpretations are that the ship has arrived before it has left, violating causality.
One interpretation says it is OK to travel and explore space at FTL speeds. This reference provides some possible implications of that scenario. Some Thoughts on the Implications of Faster-Than-Light Interstellar Space Travel.
The other interpretation often implies causality violation is impossible due to the paradoxes involved, and therefore by implication FTL travel by any means is impossible unless there is a way to avoid the potential paradoxes.
This author explains the FTL causality violation with communication.
Why FTL implies time travel
These authors show that FTL does not necessarily create a causality violation.
Faster than light motion does not imply time travel
Who to believe?
Mr. Tolley:
Agreed – I too have been waiting for a “professor” to arrive and resolve the problem that I posted, which I have been repeatedly clarifying.
You have now brought in, not one, but two “professors” :
1. Matthew Buckley, who sees the same problem that I see, though I find his explanation needlessly complex;
2. H. Andréka et al, who have a real scientific paper, with numbers and citations and what else a scientific paper is supposed to have. And it sounds credible – they formally prove a mathematical theorem.
I hesitate to declare that people are wrong at their job. But I am baffled at the complexity of both “professors'” work. We’re dealing with something VERY, VERY SIMPLE here.
Let me try to explain it yet again. When you compare reference frames A and B, you will find that synced clocks in frame A are out of sync in B. Specifically: the trailing ones show a later time than the leading ones.
Consequently, by accelerating yourself into an appropriate frame, you can create a “time difference” between any two places. You can set its size, up to a limit. And this has nothing to do with Doppler effects or the travel time of light that you see. It’s a real effect.
For example, if you whack me with a basball bat to send me off at 0.5c towards a star, WE SUDDENLY DISAGREE on what time it is there. For me, in my new reference frame, it’s later than it is for you. Our two clocks still agree here, but we CALCULATE a different time over there.
I wrote CALCULATE in large letters because we can’t see or experience this sudden time-shift. It takes time to get there, it takes time for light to arrive from there etc. When you do the math, you’ll see that no contradiction arises. Our sudden disagreement about the time on that star is only theoretical.
But if FTL is possible, then we can USE that time-shift for time travel.
I too am familiar with the concept of hyperspace from the excellent writer Asimov who wrote many entertaining stories which I believe dealt as a sideline with robots and their usefulness, that I think it had to do with the three laws of robotics or something like that. But he did get into many stories about hyperspace (which he liked to call the Jump), however as far as we know hyperspace is just a science fiction tool which suggests that there is a space (“above?”) our space of three dimensions and you can jump into that and go between distant points in a flash. That would be useful. Perhaps is equivalent to what we would call a wormhole in current terminology.
All these things concerning relativity are more than just mere equations; they also require extremely detailed thinking as to what is occurring physically to be able to interpret the mathematical equations properly. I can see how there could be time reversal from the standpoint of mathematical equations that are used in formulation – but it becomes difficult for me to imagine that there is some type of ‘past time’ that we can travel to due to our motion in space.
There is something about leaving a destination and then somehow arriving before you left that simply doesn’t sit well with me no matter what the mathematics can tell you. Time moves in a forward direction and no amount of motion, which affects the arrival of light waves, can convince me that you have actually moved backward in time. The subject is rife for careful study. Can you Alex explain to me how your FTL ship can leave your destination and arrive before you leave-in simple English that is?
This has nothing to do with “the arrival of light waves”.
Yes, we see Doppler effects, time delays and other optical illusions when things have great speeds and distances. But they are not relevant.
>> “Can you [or] Alex explain to me how your FTL ship can leave your destination and arrive before you leave-in simple English that is?”
Certainly! Explaining things is my talent. Understanding them is my other talent.
The first thing to say is that Space and Time are not separate things. They are a single fabric. You can rotate to face more or less in the Time direction or a Space direction. In practice, that means trading off distance against time.
The famous example is the “twin astronaut”. One twin stays on Earth, the other travels and returns less aged. Why?
They both made a journey between two points in spacetime, Departure and Return. The Earthbound twin didn’t move, so he travelled from D to R entirely through time. The space twin, on the other hand, covered a lot of distance, and therefore he covered less time.
And now to answer you.
Relativity says that you can’t travel faster than “c”. But some people imagine that we can, and they don’t see a problem with it. They imagine that you simply leave Earth, and arrive later at some star, and your travel speed hapens to be above a “c”. What’s the problem with that, they ask.
My reply is to construct a problem.
I take two journeys (outbound and return), and I rotate them in spacetime to make a specific trade-off between time and distance. The elapsed time of the round trip then adds up to a negative number.
Alex:
You asked “whom to believe”. My answer is : don’t believe H. Andr ?eka1, J. X. Madar ?asz1, I. N ?emeti1, M. Stannett2 or G. Sz ?ekely1 (the authors of the paper that you linked to). Their paper contains a mistake, which I will now explain.
First, remember that I constructed an example of Time Travel, giving you the times and distances involved. (I will spell it out in more detail on request.)
The important thing is this: my example involved a spaceship making a “round trip” – an outbound journey plus a return journey, both of them FTL.
Now, the authors of the paper decided to work in a 2 dimensional space, with only a single axis of Space and of course the axis of Time. They made this decision to simplify the diagrams etc. And they assumed it would have no consequences.
But there is a consequence. With their 2 dimensional world, the authors created a distinction between Left and Right. This is important because of my round-trip. I need to go Right and then go Left, to achieve time travel.
Now, look on page 5, at their “proof” of Theorem 1. They say:
“we may assume, without loss of generality, that the future quadrant of….FTL observers is right”
They won’t allow me to go left ! They don’t allow my ship to make the return trip ! But in the real world there IS no hard distinction between directions. I can turn the ship around gradually.
And if I can’t go “left” , then all of the numbers are positive, they can’t make a negative sum, and presto! There’s no time travel! I can’t do it because they arbitrarily FORBADE me to do it !
I’m sorry, Hungarian Academy of Sciences and University of Sheffield, but your boys have dropped a turd on us.
Exactly right.
I’m very behind in follow ups on this comment thread but I did find time yesterday to follow the links charlie provided. The same error David describes appears in a different form in the other link, the one to a physicist’s blog, although it takes a slightly different form.
When you tilt your line from 44, through 45, to 46 degrees on a 1+1 spacetime diagram you are playing a simplistic geometry game, and not doing physics. When you see this bit of legerdemain being performed you have to ask yourself: how did he do that?
The physics is in the answer to that question, and none of the authors does that.
The way in which Alcubierre made the effort to answer the “how?” question is very interesting, though deeply flawed as others later demonstrated.
Ron;
I’m not sure that I made it clear, just how messed up that paper is. So I will spell it out.
The authors define “Time Travel” as experiencing a sequence of events that loops back on itself. The final event must be the first event.
So, obviously, you have to go back to where and when you started, in order to Time Travel. Which, they say, is impossible.
Then they give you this 2-dimensional world to play in, but they FORBID YOU TO TURN AROUND.
How can you get back to where you started, if you’re not allowed turn around? It’s THAT stupid.
Quote by Charlie: ” Einstein’s equations are meant for a very specific set of physical circumstances and cannot be applied universally. ” No. General relativity controls the physics of our universe on the large scales and is universal. You might want to study it. https://en.wikipedia.org/wiki/General_relativity
An Alcubierre warp drive was designed by him, Miguel Alcubierre plugging into the equations of GR which uses non Euclidian Geometry or curved space time which is what a geodesic is, a curved path through space-time.
Special relativity does not include extreme curvature and it does not invalidate FTL as you imply or even causality. Einstein dismissed Kurt Godel’s time travel idea on physical grounds. Hawking had the chronology protection conjecture, but I don’t think that is needed to refute the so called causality violations. for GR and the second law of thermodynamics is enough to support Einstein’s view.
@charlie I think you are spot-on, thank you for putting the effort in and getting that insight! Of course! Anything FTL would be undefined in SR, like divide by zero or tan 90. I’ve been following the discussions and reading the papers, lots of math but not enough physics! For instance, the Alcubierre idea was based in inflation or hubble expansion where distant objects move away at apparently faster than light speeds, but its not clear how this warp drive is supposed to work at any speed, e.g. from Earth to Centauri, I expand space behind me and destroy space in front of me, *in a straight line*!? I do my thought experiments on a 2+1 rubber balloon and i’m trying to imagine how this would work. On my balloon I imagine inflation ok, and two points moving away from each other faster than c ok, and a vibration in the balloon skin would move at c and be called a gravity wave, but when I think of a bubble in my balloon skin, (i.e. the alcubierre metric picture that we see looking like a wave and flat then a trough) it would move at c as well, not FTL. And also for a soliton (which I think of as a self-propagating self-sustaining wave, a bit like a glider in the game of life) , that moves at c. But its difficult to imagine a straight line expansion from A to B on a rubber balloon. And although inflation, hubble expansion and dark energy are all observed examples of space expansion, is there an example of space destruction? i.e. the front bit of the drive, the trough, the sucking-in-space faster than light to shorten the distance.
BTW, I’ve really enjoyed all this discussion on here, educational and fun, and makes us all question our understanding of whats going on, just remember the map is not the territory, the math is not gospel, and my rubber balloon universe rocks!
There is no destruction of space in an Alcubierre warp drive. I don’t think one can destroy space or even energy, the first law of thermodynamics. There are some crude analogies of what happens to the space in a warp drive, but they really are analogies one has to take with a grain of salt like the idea that space is disappearing behind the spacecraft and appearing in front of it. This is true, but no space has been lost just stretched. One is really creating a geometry in space by changing the energy conditions locally. Changing the shape of space makes any matter in it move. With the warp drive one is making the space move around the local space reference frame but only locally. A better way of describing it that one moves one’s whole local space reference frame with the spacecraft trapped inside to so SR is not violated locally inside the bubble.
Some further reflections on this entire FTL paradox:
I reviewed one of the suggested links in the above comments with regards to the title:” why FTL implies time travel”. This particular link goes to webpage in which there is a fairly good explanation of cause-and-effect reversal, and what I learned further was that in some cases (depending upon the scenario) there exists the issue where someone will receive a FTL signal such as a radio transmission by FTL means, which will then be followed by information which is being broadcast by a light signal.
What I learned out of this was the fact that rather than some type of time travel, what we are seeing here is the effect of time dilation on a moving observer relative to a stationary observer and this particular time dilation results in getting an FTL signal at some time followed by a ordinary light signal at the speed of light at some later dilated time. This brings into the question of whether or not we are talking about troop time travel which would seem to imply that a situation ends up arriving after a journey before they left, but it’s an interesting take on why we seem to have a reversal in causality.
Time dilation only applies to special relativity. There is no time dilation for an inertial or non moving frame which is what the inside of the warp drive local space bubble is. The argument is whether there is some kind of way through hyperspace to access other dimensions or go back and forth in time like through worm hole or something. I like the idea, but I think it is invalidated by general relativity. I don’t want to go into the details as I am saving it for one of my own papers.
The multiverse idea has been used to remove the paradox so one goes back to an alternate universe and I am biased against the multiverse which represents all possibilities or the imagination, but also includes the limitations of physical reality and physics. I actually e mailed Stephan Hawking eleven years ago about his idea of virtual universes in his book Grand Design. I said they are not real ones, but only abstract potentials or “still born” or better unborn universes. The reason being is that all possibilities include potentially and the unreal but physical reality only includes the physical laws of our universe. Remove those and you don’t have a real, physical universe, but only the imagination. For example: In probability like in quantum mechanics every possibility exists in abstract form in numbers simultaneously, so we don’t need a whole new universe to express each eigenstate or each probability. We see the same thing with a quantum qubit electron. We don’t need a whole universe for every spin angle between zero and one. We only need one universe, but it must be considered to be infinite though. When the mathematics describe actual concrete things like a roll of two dice, the limitations of physical reality force one to only see two numbers at a time through the movement of time. All the possible outcomes exist simultaneously, but we don’t need a new universe for every number or side of the square dice.
I like the idea of time travel, but we don’t need to have it to learn about our past and future. In metaphysics, and parapsychology, with the ideas of precognition, telepathy, clairvoyance, etc., according to C.G. Jung and his theory of synchronicity, the psyche can achieve time travel due to its non spatial and non temporal quality to transcend space-time or be outside of space time. The psyche does not use any physical forces, so it won’t be considered to be real with a view limited to physical reality. Consequently, time travel can only be invalidated by physical grounds or principles, but supported by metaphysical ones. Jung thought of a world or dimension where the laws of physics don’t apply.
Quote: >> “in quantum mechanics … we don’t need a whole new universe to express … each probability. ”
I’ll try to explain where that idea comes from.
In QM, the behaviour of an object is described by a “wave function” that includes all possible outcomes.
But when we “measure” the object, or rather, when further information about it can reach us, the wave function does not “collapse” into a single outcome, as some say.
Rather, it blends into the wave functions of whatever it interacted with. Therefore, all of its possible outcomes lead to all possible measurements, and all possible results, and all possible consequences, and this spreads out at up to the speed of light.
If it goes on for long enough, the wave function will define a universe for each possible outcome of that single object’s single interaction. But it doesn’t always go that far.
Very elegant way to explain this and the universe and everything in it is part of the wave function. A very good book on the subject:
Ruth E Kastner. Adventures In Quantumland: Exploring Our Unseen Reality. World Scientific Publishing Company. Kindle Edition.
Geoffrey Hillend,
I wanted to clarify what was meant by my remarks regarding time dilation that I brought up in the above paragraph. Without repeating the link that tied me to what was previously brought up, you can find the link elsewhere in this particular comment section when it was being considered whether or not time travel was or was not part and parcel of FTL motion. Two links to two different websites/papers was provided by someone, and I had reference being made to the particular website as to why FTL motion incurred time travel. It was a very well done set of explanations given and there was reference made to how what we call time travel was in fact time dilation. In this fellas website he mentioned the use of a combined FTL signal as well as ordinary light to transmit information. And one of the participants in the motion was moving in ordinary space (he was not stationary) so in fact there was time dilation.
However this is not my principal reason for responding to you; just as an aside I’ve been watching a show on Amazon prime: “Project Blue Book” which purports to be a series of incidents which have been lifted directly from Project Blue Books files which was officially closed in 1970. In any event, there is a tremendous amount of presumably contacts of the first kind, which in UFO circles is supposedly visual sightings of high-speed crafts in our atmosphere. Supposedly these luminous objects move at tremendous of velocities and accelerate at speeds which would under normal conditions result in the occupants being flattened as a thin film on the interior of their crafts if ordinary Newtonian mechanics should apply.
As we have been talking about here in this comment section about FTL travel in which occupants of warp drive feel absolutely no forces within the interior of the craft as it is moving, I can’t help but wonder whether or not you might agree with me and feel that perhaps what we are witnessing (if sightings are to be believed) is FTL motion able to be accomplished in our own atmosphere by aliens (if they exist) using the very principles which have been recently been brought the light by this professors researches? Have you ever reflected on whether or not we have possibly just come across the very essence of how these presumable aliens actually make such incredible acrobatics-even in our own atmosphere?
I don’t believe this professor has proposed something that would actually work – and I’ve been saying why.
And I’m very sure that we’re not seeing, or imagining, FTL motion when we see these alleged UFOs. Have you any idea how fast the speed of light is? The maneouvring UFOs are, by all accounts, about 100,000 times slower.
What about the accelerations that would leave pilots “flattened as a thin film”? Well, that’s only going to happen if you apply the forces to their bodies from outside. What if you could accelerate every nucleus in their bodies at once? They wouldn’t feel a thing.
“And I’m very sure that we’re not seeing, or imagining, FTL motion when we see these alleged UFOs. Have you any idea how fast the speed of light is? The maneouvring UFOs are, by all accounts, about 100,000 times slower.
What about the accelerations that would leave pilots “flattened as a thin film”? Well, that’s only going to happen if you apply the forces to their bodies from outside. What if you could accelerate every nucleus in their bodies at once? They wouldn’t feel a thing.”
Once again I feel like my main point has been missed when I attempted to write down my thoughts in a cogent manner. With regards the UFOs I was merely stating that given what this article was about which was mainly FTL motion, I was attempting to convey that the same physical circumstances that would permit FTL motion (and as an accompanying phenomena-no accelerations felt by occupants) presented here in this article COULD account for STL phenomenon in our atmosphere by possibly alien craft which would use the same physical principles but at far, far slower speeds than those of light, for slower speeds than those of light but enormously faster than anything earthly aircraft could ever possibly achieve at this time. Thus the occupants of these alien craft would use the same FTL propulsion principles which would permit non-acceleration to be felt by the occupants of the craft moving in our atmosphere as they would if they were moving at FTL velocities. That is what I was trying to convey.
Secondly, I have concluded that I see nothing that’s been presented so far as to indicate to me that moving relative frames would in any fashion constitute time travel as has been exhaustively outlined here in the comments section. The best that I can say, based upon my level of knowledge and exposure to physics is that you wouldn’t have ‘apparent’ indications that you had violated causality. However I do not believe that regarding the proposition that you could return in time before you left from your initial departure point is going to be shown to be happening just because one achieves FTL velocities. And believe me I have thought about this a considerable amount of time and there’s nothing that I have seen or read that indicates that the situation which has been so aptly defended here by others is in fact a true outcome for this physical situation. So, that’s pretty much my take on the matter as to how I believe these situations would play out. It should be remembered, that this scientist is not talking in any fashion about the effects of FTL motion with regards to causality violations, rather he is by his work showing that FTL motion could be achieved if the right physical circumstances should prevail.
Electronic packages have been subjected to tens of thousands of g’s. So rather than posit some exotic drive, perhaps this would be better explained by remotely piloted vehicles or by machine pilots. Of course, your observation assumes that UFOs are a reality, despite the lack of physical evidence after nearly 75 years since the first “flying saucer” report over the USA. We have more hard data about ‘Oumuamua than all of the UFO sightings and investigations combined. But at least UFOs did result in a “genre” of mostly B-movie SciFi movies in the 1950s. (My favorite is “This Island Earth”).
“Electronic packages have been subjected to tens of thousands of g’s. So rather than posit some exotic drive, perhaps this would be better explained by remotely piloted vehicles or by machine pilots. Of course, your observation assumes that UFOs are a reality, despite the lack of physical evidence after nearly 75 years since the first “flying saucer” report over the USA. ”
Agreed, but if the vehicles are piloted by organic beings?
The pt. is that if they are real and organic beings are on board then we need to explain the ability to maneuver like that. That what I was suggesting. It’s strange there’s
no physical evidence after nearly 75 years since the first “flying saucer” report – not even a crash ?
A reminder that UFOs are off topic here, as per the comments policy. I let numerous other sites handle the question as a practical matter, past events having demonstrated that this is a topic that quickly takes over threads focused on other matters. It also clogs my email with decidedly non-scientific material.
One does not need a universe for each possible outcome because they already exist simultaneously in abstract, mathematical form. For example a computer and especially a quantum computer can make the calculations based on all possible outcomes, but someone who was too stuck in the concrete mind or maybe the imagination would think we would need a new universe for every probability, but we don’t only time and one universe or a good computer. Once something enters into physical reality, it has to take a specific measurement. It does collapse the wave function for without that collapse one will not know anything about the wave or particle. It could be anywhere. The non locality of quantum field theory only works on the small scales, but not on the large. There is no non locality on the larges scales in physics, but not metaphysics. Such an idea is banished from physics, A. Zee, 2013, based on first principles special and general relativity so there are no principles to support it. One can’t make up ones own principles in physics, but that is what I think the wave function of the universe theory is or non locality applied to the large scales. I didn’t at first, but when I read some foundation books in quantum field theory and SR and GR, I changed my mind on that, but science fiction and quantum mysticism still have an appeal due to archetypal projection so that there is some truth to them, but it is psychological or metaphysical truth, but not physical truth. I don’t want to go into this since it is off topic, but I do stick try to stick to the principles of physics when it comes to the ideas when it comes propulsion science and follow Occam’s Razor when it comes to the multiverse. Somethings are possible only in the imagination which represents all possibilities and potentials which include the real and only imaginary but only in potential.
But then you have to explain where all that computation is being done if quantum computers reach their answers that much faster than traditional machines. The answer has to be correct rather than falling into just one state. Unlike, say protein folding, there are no equivalent processes that allow quantum calculation of the 2 primes for cryptography. Everett’s many-worlds interpretation of the quantum world, however counterintuitive, does account for quantum effects.
I don’t think a debate about QM belongs on this Relativity page, but I want to say this: “collapse the wave function” is not a valid concept.
For one thng, tt does not appear anywhere in the equations of QM. You can look in them and find Entanglement, for example. But not “collapse”.
And secondly, the concept of “collapse” doesn’t make sense. It’s easy to set up examples where “collapse” contradicts itself or cannot be used to explain what happens.
Take, for example, this sentence of yours:
“Once something enters into physical reality, it has to take a specific measurement. ”
When does a loose object return to “physical reality”? When we measure it? What does “measure” mean? Is it when we touch the object? Suppose it touches another object that is also flying around loose. Will they both return to “physical reality”? If they don’t, then let me add more and more objects until I have a nice little fishing boat with a freezer. You’re telling me it’s not “real” ?
Transactional interpretation of quantum mechanics (TIQM).
The transactional interpretation of quantum mechanics (TIQM) takes the wave function of the standard quantum formalism, and its complex conjugate, to be retarded (forward in time) and advanced (backward in time) waves that form a quantum interaction as a Wheeler–Feynman handshake or transaction. It was first proposed in 1986 by John G. Cramer, who argues that it helps in developing intuition for quantum processes. He also suggests that it avoids the philosophical problems with the Copenhagen interpretation and the role of the observer, and also resolves various quantum paradoxes.[1][2][3] TIQM formed a minor plot point in his science fiction novel Einstein’s Bridge.
More recently, he has also argued TIQM to be consistent with the Afshar experiment, while claiming that the Copenhagen interpretation and the many-worlds interpretation are not.[4] The existence of both advanced and retarded waves as admissible solutions to Maxwell’s equations was explored in the Wheeler–Feynman absorber theory. Cramer revived their idea of two waves for his transactional interpretation of quantum theory. While the ordinary Schrödinger equation does not admit advanced solutions, its relativistic version does, and these advanced solutions are the ones used by TIQM.
In TIQM, the source emits a usual (retarded) wave forward in time, but it also emits an advanced wave backward in time; furthermore, the receiver, who is later in time, also emits an advanced wave backward in time and a retarded wave forward in time. A quantum event occurs when a “handshake” exchange of advanced and retarded waves triggers the formation of a transaction in which energy, momentum, angular momentum, etc. are transferred. The quantum mechanism behind transaction formation has been demonstrated explicitly for the case of a photon transfer between atoms in Sect. 5.4 of Carver Mead’s book Collective Electrodynamics. In this interpretation, the collapse of the wavefunction does not happen at any specific point in time, but is “atemporal” and occurs along the whole transaction, and the emission/absorption process is time-symmetric. The waves are seen as physically real, rather than a mere mathematical device to record the observer’s knowledge as in some other interpretations of quantum mechanics.[citation needed] Philosopher and writer Ruth Kastner argues that the waves exist as possibilities outside of physical spacetime and that therefore it is necessary to accept such possibilities as part of reality.
https://en.wikipedia.org/wiki/Transactional_interpretation
I apologise for abetting the drift of this page towards QM and away from relativity. But please let me say this : Cramer is wrong.
That link you provided, Mr. Fidler, to John Cramer’s paper, does not negate the Many Worlds interpretation.
Cramer says the Afshar experiment is the disproof – where interference exists upstream in a light beam, while downstream we collect “which-way” information.
Look at his logic : he says the grating SHOULD absorb 6% of the light (i.e. no interference) BECAUSE we collect the which-way information later.
But the information comes from photons that missed the grating. Think about it. You can’t expect that a photon who missed the grating, should somehow be 6% absorbed by the grating. It either hit it or missed it. Cramer lost sight of this important fact: each photon is an individual.
The Afshar experiment should be treated as TWO experiments running concurrently. One of them consists of photons that hit the grating, and the other consists of photons that reach the lens. One experiment shows interference, the other does not. There’s no problem.
“In this interpretation, the collapse of the wavefunction does not happen at any specific point in time, but is “atemporal” and occurs along the whole transaction, and the emission/absorption process is time-symmetric. ”
And:
“… Philosopher and writer Ruth Kastner argues that the waves exist as possibilities outside of physical spacetime ….”
Doesn’t sound like relativity to me …
I apologize for the mistake. Non locality exists in physics which is what gravity is. It was instantaneous action at a distance which was banned from physics since gravity is limited to the speed of light. Ibid.
I don’t wish to argue any ideas in quantum mechanics or microphysics. One accepts the rules does doesn’t. According to the laws of physics, if one changes those rules, they won’t be an accurate description of physical process in reality. It’s o.k. me me if some people disagree with those rules, as it is o.k. to stick to them. I will say that quantum mechanics and quantum field theory have been built up by the empirical observations of many scientists so one is not going to change some part of them that is considered important like the collapse of the wave function. If you think it can it is o.k. with me. In my opinion, I don’t think it can be removed without collapsing the foundation of quantum mechanics.
Mr.Hillend, I fear that you have been misinformed, perhaps by an outdated textbook, perhaps by “science journalists” who are not qualified to write what they do.
The truth is : “collapse of the wave function” is NOT considered a part of QM. And why should it be? The equations of QM don’t contain it. Go and look for it: you won’t find it there. Like the “three wise men” who everybody knows about, until they read the Bible which doesn’t say “three”.
“collapse of the wave function” was an early interpretation of QM, a way of visualising it. And it has been abandoned because it simply does not work. I could spell out scenarios, “thought experiments”, to prove that it does not work.
https://en.wikipedia.org/wiki/Quantum_state
That page does not discuss “collapse” as such.
However, it references another page that is explicitly about “collapse”.
Among much else, it says this:
“The existence of the wave function collapse is required in
the Copenhagen interpretation
the objective collapse interpretations
the transactional interpretation
the von Neumann interpretation in which consciousness causes collapse.
On the other hand, the collapse is considered a redundant or optional approximation in
the consistent histories approach…
the Bohm interpretation
the many-worlds interpretation
the ensemble interpretation
The cluster of phenomena described by the expression wave function collapse is a fundamental problem in the interpretation of quantum mechanics, and is known as the measurement problem. ”
I stand by my statement that “collapse” doesn’t work properly.
I posted the quantum state because I think the Copenhagen interpretation is the only one which best accurately predicts observations. Seven years ago, I already studied the other interpretations you posted here and I don’t agree with them.
What I discovered is that in order to make a space warp, one needs a quantum theory of gravity. I don’t think quantum mechanics harmonic oscillator theory will work. None of those other interpretations will work either. Quantum field theory also is not background independent and is non renormalizable. https://en.wikipedia.org/wiki/Graviton#:~:text=In%20theories%20of%20quantum%20gravity,with%20renormalization%20in%20general%20relativity.https://en.wikipedia.org/wiki/Graviton#:~:text=In%20theories%20of%20quantum%20gravity,with%20renormalization%20in%20general%20relativity.
https://en.wikipedia.org/wiki/Wave_function_collapse
I’m quite puzzled by your comment.
“Copenhagen” is one of several interpretations of QM. An interpretation is not a theory – it’s a way to explain or visualise a theory.
All interpretations of QM are attempts to explain the theory of QM. And since they all incorporate QM theory, they all make the same predictions – or, they’re supposed to.
You’re telling us that “Copenhagen” makes better predictions than the rest? Could you explain please?
I was hoping you wouldn’t ask me that question. Let’s just say the I think the Copenhagen interpretations is the foundation of quantum mechanics according to quantum physicists. If you change some crucial parts of it, then it doesn’t work or falls apart which is like any other first principles in physics.
To be fair in all of these interpretations, the Copenhagen interpretation doesn’t predict better than all of them, but only most of them. There is a flaw in all of these, so that if I plug them into the qualitative system of first principles, I can rule them out. I will briefly point them out. In the objective collapse interpretation, the idea that the Schrodenger equation does not show a superpostion of many outcomes and they must always be definite is had to swallow considering quantum mechanics. There are just too many examples that show non locality on the small scales. There is no quantum entanglement without superposition. There is no probability without superpostion when the answers are always define which is objectionable. The Heisenberg uncertainty principle of position versus velocity or momentum is based on mixing waves and superposition. When one collapses the wave function, from a superpostion of many states into a single one.
With the Bohm interpretation or “pilot wave theory” does not explain the double split experiment which is best explained by the wave particle duality and the Feymann sum over the history’s which shows a single particle always follows every path and simultaneously goes through both slits.
The many worlds interpretation is made superfluous by probability which exists in abstract form of mathematics, but only applies to the small scales so we don’t need a new universe for every probability, just one universe and time. The imagination represents all possibilities, for some are real physical process and some on not or non sensical. All the possible rolls of two dice exist in potential in mathematics, but in reality, they can only be expressed two numbers at a time so one does not need a new universe for each roll outcome or roll of the dice that did not come up, but time and new rolls of the dice.
The ensemble interpretation only looks at the total system, but not individual interactions like the difference between the Langrangian and Hamiltonian. I forgot my reason I had for this one as it has been a while since I looked at these, but it’s still missing something.
I’m sorry but I can’t reconcile all of your descriptions with the things that you’re describing.
e.g. you say about Many Worlds:
“…we don’t need a new universe for every probability…”
But MW doesn’t propose a new universe for every probability.
Just read the Wikipedia page. I quote:
“To perform a measurement on S, it is made to interact with another similar system M. After the interaction, the combined system can be regarded as a quantum superposition of two “alternative histories”….”
See that? We didn’t get a new universe. We got a new copy of the object “M”. The rest of the universe is not immediately “split” by the “measurement”.
Also, if you are sure that “Copenhagen” is the best interpretation, I will ask you what flavour of it do you mean? According to Wikipedia (again) “There is no definitive historical statement of what is the Copenhagen interpretation”.
To me, the “Heisenberg Cut” is a clear demonstration that “Copenhagen” just doesn’t work. What are the conditions under which “collapse” will happen? Using the “cut” you can make it either happen, or NOT happen, just by moving things around.
Of course you could decide that “collapse” is subjective – it does happen if you’re on the inside of the “cut” AND it does not happen for you if you’re on the outside.
But that amounts to a Many Worlds interpretation, doesn’t it.
I don’t mix my histories of universes with particle histories or the large with the small which was a problem with Stephen Hawkings virtual universes because only a virtual person can go back in time but not a real one. Also the Von Neuman interpretations is considered pseudo science by most quantum physicists. One’s eyes can collapse the wave function because there is no beam of ERM, waves or no messenger particles coming off one’s eyes to bounce back like the echo of a radar like an electronic detector to detect a particle and the wavelength of some matter particles, electrons etc and short wavelength photons of EMR are much smaller than the visible wavelength so there are invisible to the naked eye so consciousness can’t collapse the wave function but only an electronic detector.
I left out the Transaction interpretation. One has to believe in time travel for particles, Einstein bridges and the many worlds or multiverse in order for the Transactional interpretation it to work. My rebuttal is as follows: When one looks at an abstract sheet of paper of a Feynman diagram , one can imagine the beta minus decay going in reverse. In order to work in reality, the second law of thermodynamics is violated. It takes energy to reverse the beta minus decay. The proton decays into the neutron be emitting a positron and a neutrino to carry away the positive charge of the proton. These have to be recombined to get back the original proton. In our universe if that happened, then we would see it or the proton could not change into a neutron. IF we throw the energy into an alternate universe, the neutron immediately decays into a electron and neutrino in this one which does not match observations. The energy has to go somewhere and come from somewhere. What is missing from the Feynman diagram is time and the consequence of the decay, the laws of thermodynamics. It’s assumed to not in violation until one considers all the variables in the thought experiment.
Once again, I cannot reconcile your description with the thing that you’re describing.
You speak of “beta minus decay going in reverse”.
Fine. I know what that means. It literally means running the decay backwards, so:
proton + electron + antineutrino => neutron
But then you write your description and it’s… different. It’s a different decay.
In quantum mechanics, you have four variables, time, energy, position and velocity or momentum. Quantum mechanics uses the second law of thermodynamics which includes the wave function collapse. Consequently, any particles going back in time would require energy. For example. If a neutron decays into proton but we reverse than going back in time we have to end up with a proton back in time. The problem with that is someone who in the past or an alternate universe has to see a proton coming out of nowhere which violates the conservation of energy in quantum mechanics. If we subtract the energy of a proton from a neutron we get a positron and neutrino in the present which is why I said the neutron instantly decays into a positron and a neutrino. Why don’t we see protons coming out of nowhere from the future? Because there are not any and particles, and photons can’t go back in time due to the conservation of energy. I like the idea of virtual particles going back in time. I also have not mentioned the energy needed to reverse the direction of the particles. I would like to have more than a virtual self going back in time.
Also with the Transactional interpretation of Feynman diagram of the decay of a particle, if we through all of the energy into an alternate universe, then the particle must disappear from this one which does not match observations.
Ok, Let’s see the universe supposedly start with the big bang and what does a bang produce… waves. So right now we are standing on the wave front and everything arounds that is physical are trapped standing waves. Why do you think the electron/positron is what forms from a certain Gama ray frequency and energy? The local light speed is just that local. The universe is made up of many different mini bangs and light speed varies depending how long ago they where created. The speed of light is directly connect to how old the matter is in a local area from the time of creation. This is what we see and measure but outside in the space time fabric there is no restriction caused by light’s speed. We are locked into our local standing wave time created by wave front we are in. Just my own little philosophy… ;-}
I was wondering , what makes you believe those solutions won’t ever be engineered ?