My view is that the spacecoach, the subject of renewed discussion below by Brian McConnell and a design he and Alex Tolley have created, is the most innovative and downright practical idea for getting crews and large payloads to the planets that I’ve yet encountered. It’s low-cost and uses ordinary consumables as propellant, dramatically revising mission planning. Brian and Alex have continued refining the concept, as explained below in Brian’s essay on a modified version of the rocket equation. Have a look and you’ll see that planning long duration missions or missions with larger crews becomes a much more workable proposition because more consumables translate into more propellant. Could the spacecoach be our ticket to building a space-based infrastructure, with unmistakable implications for even deeper space?
by Brian S McConnell
The spacecoach, first introduced here in Spaceward Ho! and A Stagecoach To The Stars and on spacecoach.org, is based on the idea of using consumables waste streams, such as water, CO2 and gasified waste, as propellant in solar powered electric engines. The idea is to turn what is normally dead weight (and a lot of dead weight on a long duration mission such as to Mars) into propellant. This in turn leads to dramatic reductions in mass, and thus mission cost, because a ship that uses waste from consumables as propellant no longer needs an external stage weighing several times as much to push it to its destination. (If you or your colleagues are working on electric propulsion systems and have test data and citations to share see below)
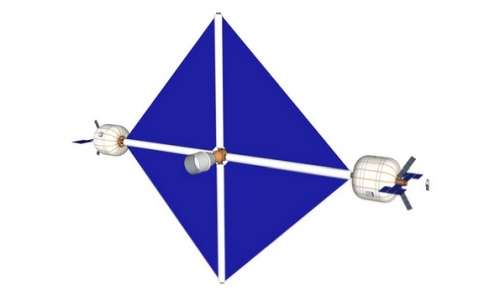
Image: The spacecoach. Credit: Rendering by Rüdiger Klaehn based on a design by Brian McConnell.
To understand the impact this has, we developed a modified version of the rocket equation that leads with the crew consumable requirements for a given mission, and then calculates the level of engine performance required to fly the mission using only consumables waste streams (mostly water and carbon dioxide) as propellant. This, in turn, yields a minimum mission cost, as no surplus propellant is required, so the mission cost is reduced to the cost to deliver the crew and consumables to the starting point (while the ship itself is reusable so its construction and launch cost can be amortized across many missions).
The rocket equation, shown below, predicts the ship’s delta-v (change in velocity), as a function of specific impulse (a measure of engine performance) and the ship’s mass ratio (starting mass divided by ending mass).
![]()
The spacecoach equation, shown below, predicts the minimum exhaust velocity (or specific impulse) required for a cost optimized mission as a function of its delta v and consumables budget.
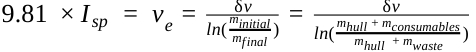
For programmers, this can also be written in pseudocode as:

Let’s consider a ship that has a 40,000 kg hull mass when empty that is being resupplied for a trip to the Martian moons from EML-2 (Earth Moon Lagrange point 2). With low thrust propulsion this requires a delta-v of roughly 18 km/s roundtrip. The ship has a six person crew, with a 15 kg/person-day budget for water, food and oxygen. The mission is expected to last 600 days, so the consumables budget is 54,000kg.
According to the equation, the engines will need to achieve an exhaust velocity of 21 km/s, which equates to a specific impulse of about 2,100s, assuming 100% of the waste streams are reclaimed (if engines can be made to work with gasified waste, even solids such as trash should be usable as propellant). If we assume that some percentage of the consumables waste streams (e.g. solid waste) cannot be used, say 20%, the engines will need to operate at a specific impulse of 2,900s. This is within the performance envelope of Hall effect thrusters, as well as several other electric propulsion technologies. If the engine performance is not quite good enough, that’s ok, the ship would just be loaded with more water than the crew really needs to compensate for this, or could even support a larger crew. This will increase costs a bit above the minimum possible cost, but also provide safety reserves above what the crew is projected to need.
Next, let’s compare the mass budget for a similar ship using chemical propulsion (e.g. LOX + methane). This mission requires much less delta-v as the ship can exploit the Oberth effect (aka powered flyby) when departing Earth, and on arrival at Mars. To give the chemical ship a further advantage, we’ll assume it uses aerobraking for Mars capture and for Earth return. So the round trip delta-v in that scenario is roughly 8 km/s. The downside is the engine specific impulse is much lower, about 360s for oxygen + methane. Plugging this into the rocket equation results in a propellant mass budget of almost 820,000 kg, over twenty times the mass of the empty hull. This can be optimized by shedding mass, such as waste, spent stages, etc, but not by a great deal without making compromises in terms of consumables, payload, etc (and we’ve already given the chemical ship a big advantage by assuming it can use aerobraking extensively to minimize propulsive delta-v).
Compare this with the spacecoach, where the consumables are the propellant. It would require the delivery of only 54,000 kg of consumables. This is 1/15th what is required for the conventional mission, and should lead to comparable reductions in overall mission costs. Meanwhile the mission itself is much simpler and less risky (all low thrust propulsion, no chemical rockets with catastrophic failure modes, no high G maneuvers, no aerobraking, plus the option to add more crew and/or consumables with little penalty).
The savings come from two sources. Because the consumables are the propellant, there is no need for external propellant. This effect is amplified further because electric engines have much higher exhaust velocities than chemical rockets so even the relatively small consumables mass needed by the crew is sufficient to propel the ship (if electric engines operated at a specific impulse comparable to a chemical rocket, you’d need ten times more water than the crew would consume).
And it gets even better. This is counterintuitive, but it is actually easier to plan for long duration missions with larger crews and high delta v (Ceres, Venus and the Asteroid Belt for example). This is because more consumables = more propellant = higher delta-v given the same engine performance, whereas in a conventional ship you get into a vicious circle of mass incurring more mass. Running the numbers for a 6 person, 1000 day mission to Ceres (delta v : 26.5 km/s roundtrip from EML-2), the consumables budget is 90,000 kg, and the required engine specific impulse is again in the 2000s, which suggests that a ship capable of reaching Mars will be capable of reaching Ceres due to the larger consumables budget.
And speaking of Ceres, it is an enormous water reservoir. While early spacecoaches would be supplied entirely from the Earth, developing the ability to extract water from low gravity sites like Ceres, and possibly the Martian moons, will be a priority as it will reduce the need to launch water from Earth, and thus further reduce operating costs, but even without in situ resource utilization, spacecoaches will be an order of magnitude cheaper to operate, and will be capable of reaching destinations like Ceres that simply cannot be reached by humans using chemical propulsion.
While it takes people a while to see the implications of this (the thinking about how to design a spacecraft is pretty ingrained), the math is pretty straightforward and suggests that order of magnitude cost reductions for interplanetary missions, with greatly expanded range, will be possible with this approach.
If you are working on electric propulsion technology, we are compiling data about the relative performance of different technologies and propellants, especially as it relates to the use of water and waste gases, to provide the community with an easy to search repository of SEP test data and citations. This data will be made available at spacecoach.org as well as on github. If you’d like to submit test data and citations, you can use this form. Contact Brian McConnell at bsmcconnell@gmail.com for more information.



Will the water be enough to stop radiation during the 1000 day trip to Ceres?
@Tom, water is comparable to lead for radiation shielding on a per kg basis. In our previous articles, we explore its uses for radiation shielding. It would be stored in reservoirs around the areas where the crew spends the most time, and in an emergency, could be pumped into temporary bladders to maximize the thickness of the water surrounding the crew.
So one question I had about this concept: can you use water directly as propellant in an ion engine? Wouldn’t you have to separate out the hydrogen using electrolysis so the ion engine can ionize that and accelerate it as propellant? So how would that be more efficient than using hydrogen which is mined at the port where you fuel the spacecraft? :)
I would argue that if you want to use water as propellant, a Nuclear Thermal Rocket would be a better choice. Run the water around the hot reactor core and instead of going to heat water in other pipes, the hot water is expelled out the back for thrust. :)
@neutrino78x we looked at many types of electric propulsion systems. Two promising candidates are microwave electrothermal thrusters and lorentz force thrusters, both of which have been tested with water (METs operate at a specific impulse of 900s, while ELFs were shown to work at 1700s). Most likely other technologies such as double helicon layer thrusters will work as well. As a next step, we’d like to see all electric propulsion technologies be systematically tested with water, CO2 and gasified solid waste.
Another important thing to note is that the engines in spacecoaches will be clustered, with many small (~ 10kw) units forming a large array. Apart from adding redundancy, one can use different engines with different propellants. So you might route carbon dioxide to one group of engines, water to another, and gasified solids to another, to optimize for exhaust velocity by propellant.
Nuclear thermal really isn’t attractive because the exhaust velocity is less than what low end electric propulsion systems can achieve, and then there are the politics that would realistically prevent them from being launched in the first place.
Another issue with nuclear engines is that they are effectively unserviceable. Typical designs assume no shielding on the engine and placing it at a distance from the crew module with a radiation shield between them. If the engine fails, too bad. In contrast, electric engines are serviceable in case of failure. The other benefit is that nuclear thermal engines have an Isp of less than 1000s even with H2 as the propellant. Electric engines can match that and considerably exceed that performance. We think that this makes them more attractive,
Where nuclear may make sense is to generate the power for electric engines in the outer solar system. However as solar PV increases performance, the trade off between solar and nuclear is going to push the range in favor of solar. The specific power of solar is already at least an order of magnitude better than nuclear, with the development cycle favoring solar.
I hope it is clear from the modified rocket equation that the deepest space missions favor larger crews, which seems counter-intuitive when thinking of space ships with conventional engines. This is because the water consumption (as water and liberated O2) represents the largest mass, whilst each crew member is almost a negligible non-consumable deadweight mass. Conventional rock technology emphasizes life support mass minimization through recycling. The spacecoach can tailor the recycling to match the mission, engine technology and crew size.
With water abundant in the solar system, large, spaceliner sized water ship designs might be rather like “Universe” in Clarke’s “2061: Odyssey 3”. Notably Universe refueled at Halley’s comet by simply trapping and filtering the erupting water vapor. This is a lot simpler than electrolyzing the water and cryogenically storing the LH2 and LOX.
Thank you, thank you, thank you very much for clarifying this. I have an additional question: lets say you want to launch from Earth (conventionally) unfueled an lets say you have a nice, orbital source of water, maybe from an redirected smaller icy body, fueling in Earth orbit would further cut down costs. Where would be the most accessible h2o source? Is this feasible?
@swage in situ resource utilization would indeed reduce the need to launch water to earth orbit. In our systems/economic analyses, we assume that all water is launched from Earth’s surface, as we don’t know how easy or hard it will be to access water at sites like Deimos and Phobos (better to assume it’s hard).
That said, let’s suppose that we discover that subsurface regolith there has useful amounts of water ice within it. It would be possible to extract the water by baking the regolith and reclaiming the water in a condenser. Probably easier said than done, but spacecoach operators will have a significant incentive to extract materials at low gravity sites, so we’d expect ISRU experiments to figure prominently in spacecoach missions.
Our opinion is that it will be important in the long run, but for the near term, better to base plans around all supplies being launched from earth, then build out ISRU capability incrementally.
@swage. If you mean accessible as in low delta-v to reach, then near earth asteroids, the moon (poles) and then the asteroid belt, especially Ceres.
However what we want is the cheapest source of water to refuel. If you need to mine the water to extract it from water rich rocks, or need to lift water from a planetary body like the moon, the costs may be quite high, at least initially. The nearest source of water is obviously the Earth, and as space access gets increasingly cheaper, it may be that this is the cheapest source of water, at least initially.
The advantage of dead comets or water rich bodies like Ceres is that the water is easily extractable with heat, and moving to suitable locations is efficient using low thrust, high Isp engines, rather than high thrust engines.
One could even keep the water as ice by shielding it from ten sun and just attach engines and solar collectors to move the “iceberg” to useful parking orbit. If there was a fleet of spacecoaches, I could easily imagine robotic water miners providing a flow of icebergs to cis-lunar space, requiring a small fraction of the acquired water to make the trip and return for another berg. Water is going to be needed for space hotels too, and it is likely to be easier to mine than platinum group metals from the asteroids.
To echo Paul’s comments, this idea is such a good one that I sincerely hope it keeps gaining in momentum. Especially as there don’t seem to be any leaps involved; the framework you’ve both outlined since the beginning looks to be close to using off-the-shelf hardware (current SEP engines may need minor mods if any as you’ve even mentioned). Even the details look superb, ie your use of H2O2 onboard.
I wish you both well in your continued endeavour and fingers crossed it gets the attention it deserves… sooner rather than later so we can look forward to building that solar-system wide infrastructure we envision we’ll need… my money’s on the Spacecoach idea.
One question regarding any hypothetical earliest tests… what is the minimum sized craft needed to fly an unmanned ‘proof of concept’ mission. Would a very small vehicle do it and do you have any idea at all what kind of timeframe we might be looking at for a small test mission assuming enough interest is garnered to engage you both in ‘talks’ with a ‘Big Player’ in the industry in, say, the next 5 years (horrible question I know)? Are there issues that might prevent a first test being developed within a ‘standard’ timeframe for a modern mission such as 10 to 20 years?
Surely there is a mistake in the delta-V equation:
If R = the mass ratio = [Mhull + Mpropellant]/Mhull, then
Delta V = 9.81 x Isp x LnR
Ln is of course the natural logarithm. Using the equation as given, without the natural log, gives us the ridiculous result that if Mpropellant = zero, R = 1, and no propellant is expelled, yet the calculated delta V = the exhaust velocity!
Inserting the natural log gives us the correct answer delta V = zero, since Ln1 = 0.
Greetings from an arthritic old codger with an interest in all things space related:).
Effective use of the shaded area behind the solar cells could store the ice more effectively than having a storage tank saving on mass.
@Brian, Alex
Just wondering if Ozone would make a better chemical than hydrogen peroxide, as the temperature falls the half life increases. At around -50 degrees Celsius the half life is 3 months and it is quite dense ~2.14g/cm^3.
https://www.pssurvival.com/PS/Water_Purification/Ozone/Oxone_Decomposition_In_Water_Factors_2010.pdf
@Jay – you are correct that the first equation appears to have dropped the Ln. You can see that it is correct in the next equation.
@Michael – using the PV array as a sun shield is a good idea, as long as the ice is small enough to be shaded. I was thinking of reflective foils that are low mass, with the ice looking rather like a foil wrapped chocolate :)
Not sure about the idea of O3. It violates the premise of the difficulty of storing cryo-propellants, it is toxic, it would need an H2 source to make H2O needed for consumption, and O3 would presumably need to be manufactured at the water source.
@Jay there is magic math here. All we do is use waste streams from the consumables as propellant. Given the high exhaust velocities of electric engines this eliminates the need for an external stage to push the crew and consumables around. Hence the large mass reduction.
@Mark you could validate the propulsion and power systems with an uncrewed drome that flies as a secondary payload. To simulaye the delta v of an interplanetary you just do lots of small altitude and plane changes to accrue a large delta v. Could easily be done within a few years if someone gets behind it. Another option will be to test water and sep on the planned bigelow space stations.
How stable are the proposed fabrics – the “sausage casings”- to radiation?
@Harold – Bigelow’s scale habitat version – Genesis I – has been in orbit since 2006, and Genesis II since 2007. AFAIK, both have remained inflated. I think it is fair to say that the technology for hull construction is proven. It can only get better from here on out as new materials are tested for resilience to the space environment. In our original JBIS paper we assumed hull construction based on Bigelow hab specs for unit area mass.
@Alex Tolley July 4, 2015 at 14:08
‘@Michael – using the PV array as a sun shield is a good idea, as long as the ice is small enough to be shaded. I was thinking of reflective foils that are low mass, with the ice looking rather like a foil wrapped chocolate :)’
The solar cell collector will always be larger than the ice block it shields, enormous amounts can be shielded axially away from the sun and the crew capsule/s could sit in the middle of it. The sided of the ice need only have a very thin layer of reflective material as the sun at most would hit it at a slight angle. It is a pity there is no engine that could run on chocolate efficiently, if there is one I would like to volunteer as a passenger aboard the craft however I may out compete the engine for the chocolate…
‘…it is toxic, it would need an H2 source to make H2O needed for consumption, and O3 would presumably need to be manufactured at the water source.’
I was thinking along the lines of it been dissolved into the water, it has a descent energy content and is a powerful biological sterilent.
Further I am not sure it would be a good idea to get rid of N2 and CO2 but rather recycle it via plants which would not only add to the food supply but also the ambiance.
@Michael – we tend to agree on N2 recycling. Whether it is used on board the ship or contributes to the ag stations at the destination, it would be very valuable material. I tend to think that plants for aesthetic reasons are a good idea, as are easy to grow vegetables to provide occasional fresh food, like tomatoes and hot peppers. A full ag recycling system probably doesn’t make sense when you look at the mass requirements and potential failure modes. At least with current technology.
@Alex Tolley July 5, 2015 at 15:05
‘A full ag recycling system probably doesn’t make sense when you look at the mass requirements and potential failure modes. At least with current technology.’
I agree on this, sometimes it is just better to throw the bucket contents over the side, however sterilising it before we do in case we contaminate the solar system with our biological waste to soon. By using the microwaves from the engines we could liberate the gases from the solid waste which we could collect for reuse and the water ‘vapour’ could go straight into the engines for propulsion.
I like this concept a lot, even if I feel the case is overstated for Mars. The main spacecraft shouldn’t be brought all the way down to low Mars orbit. Staying in a highly elliptical orbit or a close solar co-orbit should be used so the return delta-v is low. This does mean that the Mars ascent capsule needs extra delta-v to match the higher velocity of the main spacecraft at periapsis…but the Mars ascent capsule should be fueled by ISRU anyway, IMHO. For the main spacecraft, the round trip delta-v is not much larger than the one way delta-v.
As for what sort of electric thruster may be suitable for a wide variety of waste products, I’d look at pulsed laser plasma propulsion. This involves one or more on board lasers to heat a small bit of propellant, at a very high repetition rate. Something like this:
http://photonicassociates.com/ISBEP4-3.pdf
BTW, I am NOT assuming that water would be a waste product…it’s just too useful and readily recyclable to be waste. A more plausible waste product is methane; the ISS produces a ton of methane (per year), which is simply vented into space. It could instead by used as propellant. The ISS also produces quite a bit of solid waste, which is a reason why I suggest looking at pulsed laser ablative propulsion rather than more conventional electric thrusters. The small spot size and low penetration compared to microwave heating is critical for getting a good specific impulse. You want to heat a small bit of propellant to a very high temperature, to get the most impulse per gram of propellant.
@Isaac thanks for the citation. This looks like it could be useful for regolith based propulsion (e.g. melt and mold regolith into bars that are fed into a thruster like this and ablated).
@Alex
Ever thought of using Xenon trioxide, XeO3, dry it is dangerous but quite safe dissolved in water to form an ice. Xenon has a good impulse ~19 500*, it can be used as sterilant and the xenon could also be used as a inert gas in the space craft, many birds with one stone. Not sure of the thrust if used as a mono propellant ‘dried out more’ though, might be useful when needing to stop suddenly to reach into a capture orbit.
* https://en.wikipedia.org/wiki/Dual-Stage_4-Grid
It think this stagecoach idea has a lot going for it and thanks for sharing it with us and if you need any ideas or help just e-mail me.
Paul could you ping my e-mail address to Alex and Brian please if they would like it.
Have done so, Michael.
@Michael, our criteria for propellant is it must have first pass uses as a consumable. So this will include things like: water, frozen food (mostly water by mass), combustables (e.g. paper, discarded clothes, packaging, etc). The waste streams from these will include: water (reclaimed from condensers, urine, etc), carbon dioxide (reclaimed from scrubbers), methane (generated via sabatier reactors), and gasified waste (e.g. pyrolyzed trash). Even then the specific impulse for these propellants will probably be lower than for xenon, in an ion drive for example, that’s ok because there is plenty of mass to work with. That said propellants like xenon will make lots of sense for unmanned cargo ships, as you can maximize payload by using higher impulse engines (the tradeoff is transit times might be longer due to available power, but thats ok as you’d send them ahead of the crewed ship).
@Brian McConnell
Another possibility could be the same basic idea, but using a pulsed electron beam to vaporize a small spot of material at a time. But I don’t have any references for this concept. Maybe there’s some technical reasons I’m unaware of which make the concept impractical.
I would think it would be superior to pulsed laser ablation propulsion, because:
1) Electron beams are more energy efficient (lower power requirements for a given exhaust power)
2) Electron beam absorption is efficient regardless of target material (important when arbitrary waste products or random regolith is used)
3) Focusing elements are electromagnets which can be trivially protected from ejecta/exhaust.
4) The electron beam can be easily bent by a magnetic field into an “around the corner” path. A laser can be routed with a mirror, of course, but such a mirror could be vulnerable to being coated with ejecta/exhaust. Magnets bending an electron beam into a 180 U turn would be unaffected by surface contamination. This allows the electron beam engine to be placed in a convenient location completely out of line-of-sight with the impact point–no risk of ejecta/exhaust deposition.
The sort of hardware required for a pulsed electron beam ablative thruster is similar to the hardware used for electron beam welding.
Note that an electron beam accelerator on a “Spacecoach” could be generally very useful. Besides welding, an electron beam can be used for a type of 3D printing called electron beam freeform fabrication:
https://en.wikipedia.org/wiki/Electron_beam_freeform_fabrication
EBF3 has been tested in zero gravity successfully, and could generally be a very useful technique for various tasks in a long term manned space mission.
@isaac drop us a line. Woul like to discuss this in more detail. You can find our contact info at spacecoach.org
Spacecoach gives me a “kid in a candy store feeling”–there are so many things that it would enable (or make practical), which would in turn make the vehicle even more attractive!
Aldrin Cyclers of all types (cislunar, Mars/Earth, intra-asteroid belt), asteroid mining, even outer planet exploration (at least out to Jupiter) would be affordable and easier to do with spacecoach. Mars missions would be far more physically comfortable, *not* having to arrive via aerocapture, and having the option of centrifugal artificial gravity enroute to Mars and back to Earth. If Elon Musk, Jeff Bezos, and/or Richard Branson took a shine to the spacecoach concept, who knows what might happen, and perhaps fairly quickly? Also:
A “rough-and-ready” spaceship technology like this *has* to be developed if interplanetary (and ultimately, interstellar) travel are to become more than rare, expensive stunts. The current paradigm of spacecraft that require surgical smocks and clean rooms and volatile, toxic, and explosive propellants will -never- lead to routine space travel. Electrical propulsion engines that can be brought inside and repaired on an ordinary–for a spaceship (a “vacuum suction table,” like the improvised ones on Skylab)–workbench, with ordinary tools, are what we need, not fussy chemical or nuclear rocket engines that require specialized *everything* to service them.
Launch vehicles to get the spaceships (or their parts) up into Earth orbit also must be simple, robust, safe, non-toxic, and reliable–and *non-explosive*. Only the hybrid rocket–which burns a solid fuel/liquid oxidizer combination (LOX/synthetic rubber is nearly as powerful as LOX/kerosene)–meets these criteria, and it can also be made reusable if desired; a reusable hybrid propellant launch vehicle could be similar to SpaceX’s reusable Falcon and Falcon Heavy designs. In addition:
The Bigelow-type inflatable modules of a spacecoach ship need not be completely dependent on internal air pressure to retain their shape. Selected areas could be pre-impregnated with a vacuum-curing resin before launch (a ground-protective plastic outer sleeve could rip open during module inflation in space), to form rigid “stringers” and “rings” that would hold the modules’ shape.
Let’s spread the word about spacecoach–it’s the 18-wheeler truck (or subsonic jetliner) equivalent for space travel–it isn’t the fastest or highest-performance vehicle, but it’s a *practical* spaceship that, like trucks and jetliners, isn’t a temperamental prima donna that requires expensive, highly-specialized facilities to support it.
@J. Jason Wentworth – Unfortunately, hybrid rockets lack sufficient performance for practical orbital launch boosters. The problem isn’t so much the specific impulse (which is indeed comparable to LOX/kerosene), it’s the dead weight of the fuel tank. Liquid fuel rockets use extremely powerful turbopumps to take low pressure fluid and force it into the high pressure combustion chamber. But solid rockets and hybrid rockets can’t do that. The solid fuel tank IS the combustion chamber. That means the containment cylinder must be thick enough to hold in the full pressure of the combustion chamber. So, even though the specific impulse of all three chemical rocket types look pretty comparable, liquid rockets actually have a big edge. Launch costs and logistics also strongly favor liquid rockets over solids or hybrids.
If you want a launcher system that fits all of your desired criteria, you’ll have to look at more exotic possibilities. Maybe some form of laser launch would suit what you’d like.
Alex Tolley wrote (in response to Michael): “Not sure about the idea of O3. It violates the premise of the difficulty of storing cryo-propellants, it is toxic, it would need an H2 source to make H2O needed for consumption, and O3 would presumably need to be manufactured at the water source.”
This inspires another question that involves oxygen (partly). Might an ion or Hall Effect thruster use water, *but* in the “broken” form of OH- (hydroxide) and/or H30+ (hydronium) ions instead of neutral H20? Even if not (creating and maintaining those ionic forms might require a lot of electrical power, and/or high heat inside the engine), ordinary water could be used as the working fluid (reaction mass) in electrothermal (arcjet or resistojet) engines. Such engines, in tests on Earth, have usually used hydrogen or ammonia, but they can use water, too.
@Jason the main issue with using water in electric engines is increased losses to ionization potential and dissociation, compared to inert gases. However, these losses are relatively small compared to the kinetic energy of the exhaust (50MJ/kg to 500MJ/kg). For example, what we’d expect to see when water is tested in an engine that normally uses inert gases is that specific impulse (exhaust velocity) is similar, but thrust/power ratio is lower due to energy lost to ionization, splitting water molecules into constituent parts, etc. The engineering competition for engines will be helpful in generating data about which engines perform best and have the best overall efficiency.
@Alex Tolley
That the Bigelow units remain intact is promising – but I am reminded of a failure via microscopic cracks that were eroded to drips in an expensive chemical plant pipe installation. If test patches – say 5 by 5 cm – could be exposed a suitable length of time to the environment and checked for nonobvious damage, that would be a trivial cost compared to first mission failure. Remaining inflated in a vacuum could be simply mechanical stiffness.
Depending on the type of electric thruster, water and other similar substances may be a problem because hot reactive oxygen is created. One big reason Xenon propellant is used is to limit damage to the thruster electrodes. I suggested looking at pulsed electron beam ablative propulsion because there are no electrodes, and nothing exposed which may be adversely affected by ejecta/exhaust.
Isaac Kuo wrote:
“@J. Jason Wentworth – Unfortunately, hybrid rockets lack sufficient performance for practical orbital launch boosters. The problem isn’t so much the specific impulse (which is indeed comparable to LOX/kerosene), it’s the dead weight of the fuel tank. Liquid fuel rockets use extremely powerful turbopumps to take low pressure fluid and force it into the high pressure combustion chamber. But solid rockets and hybrid rockets can’t do that. The solid fuel tank IS the combustion chamber. That means the containment cylinder must be thick enough to hold in the full pressure of the combustion chamber. So, even though the specific impulse of all three chemical rocket types look pretty comparable, liquid rockets actually have a big edge. Launch costs and logistics also strongly favor liquid rockets over solids or hybrids.
“If you want a launcher system that fits all of your desired criteria, you’ll have to look at more exotic possibilities. Maybe some form of laser launch would suit what you’d like.”
I’ve read reports from folks in the business that say otherwise. Solid propellant rockets can and do use lightweight composite motor cases (which are larger [longer]–and therefore heavier–than the fuel grain cases of equivalent-performance hybrid rockets). The oxidizer tank weighs considerably less, and it need not withstand great pressures, as hybrids can be pump-fed rather than pressure-fed. The higher specific impulse of LOX/synthetic rubber (HTPB, PBAN, or a polysulfide rubber) hybrid motors would allow all-hybrid launch vehicles to use fewer stages than all-solid propellant launch vehicles (having an ISP close to that of LOX/kerosene, a two- or three-stage hybrid SLV could orbit as much as a three- or four-stage solid SLV). But:
Getting away from the rocket altogether (at least combustion-based ones) is, in the long run, probably the best way to make getting into Low Earth Orbit truly cheap. Ground-based laser-powered rockets using common working fluids (even water), the jet/bolo tether combination, Bob Forward’s and Hans Moravec’s Space Fountain, and (ultimately) space elevators will knock off a great many of those depressing zeroes in the prices to LEO. In addition:
Thank you, Brian McConnell, for explaining that (about using water in ion or Hall Effect thrusters) in detail; I figured that water would be better for use in electrothermal (arcjet or resistojet) thrusters. Perhaps ammonia, carbon dioxide, and/or hydrocarbons (methane, ethane, etc.) would provide higher performance than water in ion and Hall Effect thrusters (although not as good as xenon, mercury, and cesium, of course), and since ammonia, CO2 (I think), and hydrocarbons are available in comet nuclei (including, hopefully, those asteroids that are actually extinct comets), spacecoach ships using such thrusters could refuel from these bodies.
Potentially there is the use of hydrogen trapped within Bucky balls or Nano tubes. Once trapped the density of the hydrogen can reach that of the core of Jupiter which is very high. Place this in a binder to make a solid fuel and it would be very powerful not only because of the energy of burning hydrogen and carbon with oxygen but because of the stored potential energy of compression. There is also the benefit of higher temperature storage.
We are, perhaps, nearer than expected to a spacecoach. Seems the american air force is currently testing a Electrodeless Lorentz Force Thruster – ttp://msnwllc.com/space-propulsion – in the current X37B mission…
From MSWM website: “The ELF thruster, funded by the Department of Defense, utilizes Rotating Magnetic Field (RMF) and pulsed-inductive technologies that promise radical advances in space propulsion. The ELF creates, forms, and accelerates field-reversed plasma toroids to high velocity. It has demonstrated the ability to efficiently utilize complex propellants such as Martian Air, Liquid Water, and Hydrazine .
The ELF enables a broad range of high-power propulsion missions. Fundamentally, this technology has significantly greater thrust and power densities than any realizable propulsion technology. The ability to operate on in situ propellants will enable very eccentric orbit propulsion, re-fuelable orbital transfer vehicles, deep space return missions, and even direct drag makeup for extremely low orbits. At current power levels, this thruster technology minimizes system mass, size, and cost, while increasing overall mission flexibility. Finally, extending this technology to higher densities and powers that have been demonstrated in the laboratory, there are mission applications in high-altitude, air-breathing, hypersonic flight and beamed-energy upper stage propulsion that are not feasible with traditional technologies. Please see technical publications below for a complete description of experiments, thruster specifications, and results.”
This is a relatively late footnote, anyway:
The best place to get the water would be from the moon. Because of the mild gravity it would be far simpler to get the fuel for the drive from the moon surface. Of course you need an extraction infrastructure there. But it is the most efficient to get water into Earth orbit.