Heading for the hotel lobby the first night of the Breakthrough Discuss meeting, I thought about a major theme of the Breakthrough Starshot initiative: Making things smaller. Robert Forward wrote about sails hundreds of kilometers in diameter, and vast lenses deep in the Solar System to collimate a laser beam that would drive them. But Breakthrough Starshot is looking at a sail four meters across, carrying a payload more like a smartphone than a cargo ship. That big lens in the outer system? No longer needed if we can power up the sail close to home.
How to Look at Alpha Centauri
Digitization works wonders, and Moore’s Law takes us into ever smaller and more tightly packed realms on silicon chips. The trend affects every aspect of spaceflight and astronomy, as witness ACEsat, a small coronagraph mission with an explicit mission, the search for planets around Alpha Centauri A and B. Ruslan Belikov (NASA Ames), working with Northrop Grumman, led the team that conceived this mission, which was recently submitted for NASA Small Explorer funding. The funding did not come through, but the ACEsat idea persists.
At Breakthrough Discuss, we heard Ruslan Belikov describe the mission. Lead author of a recent paper on the work (“How to directly image a habitable planet around Alpha Centauri with a 30-45cm telescope,” available here), Belikov showed a half-scale model of ACEsat that was small enough to hold in your hand. The mission as currently conceived uses a 35 centimeter by 18 cm optical mirror, fits into a CubeSat, and in the view of its creators, is capable of directly imaging Earth-like planets around Alpha Centauri (see ACEsat: Alpha Centauri and Direct Imaging, Ashley Baldwin’s article from last December, for more).
“Alpha Centauri isn’t the tip of the iceberg,” Belikov told conference attendees during a panel discussion on exoplanet detection. “It is the iceberg. We know that small stars like Barnard’s Star or Proxima Centauri have small habitable zones. But nature has given us Alpha Centauri, a favorable outlier — think about how large its habitable zone appears on the sky in terms of its angular size. We would need a telescope three times larger for other stars.”
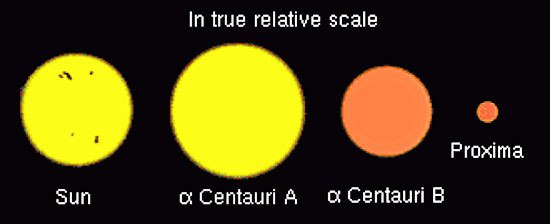
Image: Stars in the Alpha Centauri system as compared with the Sun. Credit: David Benbennick. CC BY-SA 3.0.
When asked what surprises we would find around the Alpha Centauri stars, Sara Seager (MIT) suggested that the biggest surprise would be finding a true Earth twin with life on it, and Belikov was quick to agree — “Sara stole my answer,” he said with a laugh. But Seager would go on to talk about future telescopic efforts focusing on just one object, one specialized type of telescope for each type of star. That more specialized approach seems to fit in nicely with Belikov’s ACEsat concept, tuned as it is for not just a specific type of star but a specific stellar system.
Cornell’s Lisa Kaltenegger urged the audience to think about an Earth ‘twin’ being utterly unlike what we might imagine:
“A world like this could meet our conditions for habitability and yet be much different from the Earth. We can imagine a different kind of biota taking over. When you think about an Earth twin, don’t think about the picture you know. Think yellow, think green, whatever color you want. We can look at some of the exotic deep water fish we find in the ocean and realize that they, as strange as they seem, evolved right here. What might wind up evolving around Centauri?”
Kaltenegger’s remarks drew on her work at the Carl Sagan Institute, where she has built a new interdisciplinary research group spanning ten departments. The effort includes a color catalog that examines the differing reflectivity of various planets depending on possible biota. Which gets us to a major point about Breakthrough Starshot. As Kaltenegger mentioned more than once, data return from the nearest stars needs to include more than basic photographic images. Spectroscopic analysis is crucial as we examine planetary atmospheres for biosignatures.
Natalie Batalha (NASA Ames) pointed out that while we all hoped to find planets in the habitable zone of Alpha Centauri, we might consider that a null result there could still leave us with interesting science. We have not resolved the surface features of any main sequence star except for our own Sun. An Alpha Centauri mission gives us the prospect of resolving the surface of three stars, a science windfall that adds to the benefits of the mission.

Image: Exoplanet hunters Sara Seager (left), Lisa Kaltenegger, Natalie Batalha and Debra Fischer during a break at the meeting.
SETI and Its Consequences
The question and answer sessions at Breakthrough Discuss tended to run into our break periods, when many of the issues continued to circulate. A key issue for SETI is that factor in the Drake equation that addresses the lifetime of a technological civilization. Just how long do such entities survive? It’s an issue that lies like morning fog over the SETI landscape as we look at our own problems with the proliferation of powerful weapons systems and ask what happens when small organizations, even individuals, can acquire ever more deadly capabilities.
Here Harvard’s Avi Loeb brought up a point many others had been thinking about, to judge from the ensuing conversations outside. We naturally focus on finding biological life because that is what we are, but the technologies we are discussing remind us off the possibility that life transforms at a certain level of its development into a technological phase that leads to post-biological intelligence. Sara Seager pointed to existing tools like pacemakers and artificial limbs — if life goes post-biological, how do we create a SETI capable of identifying it?
For that matter, what do we do if it’s non-biological, as Denise Herzing (Florida Atlantic University) asked. Researching dolphin communication through the Wild Dolphin Project, Herzing wonders what the signatures of a non-technological species might be. We are only beginning to understand the complexity of dolphin communication. What if a Breakthrough Starshot mission encounters a world with an intelligent, non-technologial species in charge? Is there any way we could identify it?

The SETI session itself, led by Jill Tarter, focused on optical SETI and the new directions it opens to scrutiny. Again, the issue seems timely given the nature of the Starshot initiative, for as we conceive of technologies here on Earth, we then must ask whether equivalent technologies would be visible to us. Breakthrough Starshot envisions using phased laser arrays scaling up to the 100 GW level. As we learn how to create such ‘beamers,’ we have to ask whether the most common SETI signature in the optical might not be transient pulses that are the byproducts of other activities rather than intentional efforts to communicate with us.
Image: Jill Tarter takes the podium to begin the SETI session.
Puzzlingly, Jim Benford’s paper on that very idea was put into the session on using the Sun as a gravitational lens, but the methods Benford is discussing are very much part of the optical SETI landscape. Centauri Dreams readers already know Benford’s findings: Depending on the use of the beamed energy technology, we would indeed be able to detect transient signals from another star with equipment existing today (see Quantifying KIC 8462852 Power Beaming for background). See also “Power Beaming Leakage Radiation as a SETI Observable,” available here).
Moreover, there does exist a communications dimension, as Benford explained:
“SETI messages may be found on power beaming leakage. That leakage is more powerful than any beacons we’ll ever be likely to build, so we should look at transient signals to see if there is a message embedded on them.”
Beamed energy options for an advanced civilization might involve everything from microwave thermal rockets (beaming to orbit) to orbit boosting to interplanetary and even interstellar missions. With each of these missions, you get progressively higher energy usage. And we can certainly go beyond this list of applications into areas like asteroid deflection, which might one day be necessary to adjust a dangerous trajectory using a high-powered laser. Another possibility: Using a beamer to create a thrust (by evaporation and desorption) of a comet’s surface, which might be a technique one day used in terraforming a planet like Mars.
Benford points out that given their visibility over interstellar distances, many of these uses of beamed energy should make us reconsider optical SETI strategy. Rather than focusing on narrow-band transmissions of the kind likely to be found in a beacon, we should look for more powerful beams with a wider bandwidth. Whereas earlier optical SETI work has involved the 1 ? 10GHz microwave band, we might, considering our atmosphere, want to examine bands where lower oxygen and water vapor allow transmission, which means windows at 35GHz, 70 ? 115GHz, 130 ? 170GHz and 200 ? 320GHz.
The caveat is that power beaming is not isotropic but highly directed. The geometry is not always going to favor detection — the fact that we do not see the beam does not mean that it is not there. An interesting suggestion is to revisit the thousands of transients that have been observed and are now stored in the archives of the SETI@home project.
James Guillochon (Harvard) examined rapid travel in the Solar System via lightsails powered by beamed radiation, underlining some of Benford’s points. A lightsail network in the Solar System is the kind of SETI observable Benford and son Dominic have already addressed in their upcoming paper, the point being that leakage around the edges of the sail cannot be avoided. You may recall that Guillochon, working with Avi Loeb, discussed SETI possibilities in 2015 in “SETI via Leakage from Light Sails in Exoplanetary Systems,” available here).

Image: Beautiful weather and a Palo Alto spring made the occasional break a welcome chance to relax.
But enough for today. More SETI discussion tomorrow, after which we move into the Breakthrough Starshot mission itself as described by former NASA Ames director Pete Worden, and the possibilities of the Sun’s gravitational lens as both a mission target and a mission facilitator.



This reminds me of a similar quote by Haldane, although in a different context:
partial quotation
While imagination can run riot when unanchored to data, I think we might just be a bit more conservative regarding life.
Firstly micro-organisms are likely to overlap quite well with the range of terrestrial forms, which already exhibit a very wide range in metabolic processes.
From such organisms will evolve multi-cellular life. Evolution seems to have constraints on what can evolve. This may be a path dependency based on random directions taken on the fitness landscape, or it may reflect real constraints as to what works. I think the paleontologist Niles Eldredge thought more along the lines of constraints.
If so, then ET life, while exotic, might not be as strange as we can imagine, but rather different but within the bounds of terrestrial life historically. Their fundamental biology might be based on what we already have seen on Earth.
Just as physics has rules out some exotic propulsion systems, so it might also rule out much imagined biology.
Similarly, I find this fanciful:
Has any non-technological species ever been “in charge” on Earth. Humans certainly were no “in charge” until quite recently, and this is very much due to technology. If we lost our technology, would we stay “in charge”? I very much doubt it. So by all means imagine playful non-technological species that have high intelligence, and consider how we might detect them, but we shouldn’t assume that such species will dominate. After all, cetaceans do not dominate the oceans of Earth.
While we are limited to observing the universe from home, our own history shows that nothing beats being “on the ground” to get the true picture. Historically explorers banished “dragons and mermaids” as well as other bestiaries. Our own space probes have given us exquisite knowledge of the surfaces of other worlds in our solar system. It will be the descendants of Starshot that will give us a truer picture of distant worlds and any life that they harbor.
I read “in charge” as a hyperbolic way to describe the most intelligent species on a planet, not as a fanciful way to introduce authoritarian dolphins.
The question of how to communicate, and whether we should communicate, with non-technological intelligent species emerges from convergent evolution. Nervous systems and brains are likely to be a requirement for complex multi-cellular organisms, with non-technological intelligent species outnumbering technological intelligent species.
I would argue they are, discounting humans. The only rivals I see is sharks, but the contest here seems no better than even for the sharks (http://news.discovery.com/animals/sharks/shark-vs-dolphin-battles-can-have-surprising-outcomes-140814.htm).
Intelligence alone is powerful, even when not coupled with technology. While a knife or a gun certainly works better, a lot can be achieved by simply outwitting less brainy opponents.
I think the better question here is whether it is plausible to have intelligence without tools or weapons. I think the latter follow from the former, pretty much.
Re “as we conceive of [Starshot-like propulsion] technologies here on Earth, we then must ask whether equivalent technologies would be visible to us… As we learn how to create such ‘beamers,’ we have to ask whether the most common SETI signature in the optical might not be transient pulses that are the byproducts of other activities rather than intentional efforts to communicate with us.”
Very interesting idea, but I think it underestimates the possible. Starshot-like propulsion seems the best that we can do at this moment, but I consider it quite likely that we will be able to find much better ways in the next few decades or centuries. If so, the “Starshot window” in the life of a civilization is short.
Non-technical life should be observed. That’s all.
If they’re able to reach their planetary neighbors it’s okay to at least let them find an artifact without letting them know much yet.
I think it’s basically inconceivable that we could find a nearby technological society that has not found us first. I mean, look at us, we’ve been using technology for 0.00002% of the age of our galaxy, and already we’re making plans to visit other stars. The odds are infinitesimal that around another star, some lifeforms are using laser beam propulsion but never got around to sending a probe to Sol and its planets. Why would they be doing all that high velocity spaceflight?
Thanks for getting your report of Breakthrough Discuss to us so fast, Paul, I don’t know what I’d do without you! Things have certainly heated up lately with all the funding going to SETI and Project Starshot. It’ll be interesting to see where this heightened interest in Alpha Centauri will go in the next few years.
It appears that there is the (perhaps remote) possibility we will get a fleet of lightsail probes to the Centauri stars within my lifetime, something I never expected. The most likely showstopper seems to be fitting a communication system powerful enough to reach across 4.37 lys on a probe consisting of a few grams of a electronics! Not sure how they plan to achieve that.
Nonetheless, it is a bold idea and one that demonstrates how unanticipated breakthroughs can completely change how we can carry out a challenging goal. In the early days people imagined that we would need large crewed space stations to function as communications relays and weather watching stations. You needed astronauts, of course, to change the vacuum tubes–but then the microchip came along. Now all those tasks are carried out by robotic satellites. In the early days of vacuum tube electronics, nobody could even imagine something like Starshot.
This sounds a bit downer for human missions to the stars, but I think that is the wrong way to think about it. We don’t need to send humans to change the vacuum tubes or take instrument readings, but human explorers will always outclass robots (barring truly imaginative AI) and we will someday wish to go to find new homes as well.
Instead, I wonder how unanticipated breakthroughs might completely change how human interstellar exploration might be achieved. Perhaps the idea of huge, slow generation ships is entirely wrong. Genetic engineering and reproductive technology might give us a way to maintain genetic diversity without bringing a large population. This would vastly reduce the starship’s size. Or perhaps we could figure out how to make humans hibernate, as is widely anticipated in Hollywood films. With most of the crew asleep, we could both vastly reduce the mass of the habitat and spare the astronauts the tedium of long interstellar voyages. As Freeman Dyson said (and I paraphrase) interstellar travel is as much a biological problem as it is a “hard engineering” one.
Might? Where have you been? The freezing, storage and use of semen, eggs and embryos has been common practice for decades. Simply be merging semen, you can put a million genomes in a single tube and deep freeze them to last for millenia.
re: humans ‘in charge’
We should remember that technology originated in humans chiefly because of how poorly early humans were equipped by nature to defend themselves or to obtain food. Tools came about because of the facility of thumb & fingers, stereoscopic vision, and an incredible expanding brain along with
the struggle of a naked ape to survive. Technology is just tools.
Other intelligent species might not be so poorly equipped!
There are alternatives to technology, which has its down side. Think “Dune.”
Also, consider the laughter other intelligent species will enjoy when they meet creatures from earth that think they are ‘in charge.’
An argument could be made that bacteria are “in charge”. Anyway, we dont need to solve this question of who’s “in charge”. For all we know, there may be two species “in charge”. All that matters is who’s creating the energy leakage. And what is it’s form.
I suppose the best way to define “in charge” is relatively: If the question arises whether one or the other is in charge, observe the interaction and determine who manipulates whom, or who kills whom. I think that by that definition, humans are clearly in charge on Earth, and just as clearly there is no room for a second species.
Technology originated in humans for no other reason than that humans were able to acquire, spread and accumulate knowledge over generations. That is the threshold where intelligence becomes culture. Technology is just an outgrowth of culture. In my view, it is an inevitable outgrowth, regardless of how weak a species might be, or how opposable their thumbs are.
Dolphins are pretty intelligent, but they do not have culture. One might accidentally learn how to use a tool, but they wouldn’t be able to teach others and their children before they forget, because their language abilities insufficient.
@Project Studio, I concur. We should prepare to re-define “intelligence” as well as “life” and “technology” when we venture to the stars.
I really hope this conference is uploaded online.
“A key issue for SETI is that factor in the Drake equation that addresses the lifetime of a technological civilization. Just how long do such entities survive?”
Several historians have calculated the average length of ancient civilizations on Earth. 350 years seems to be around the average length. http://hubpages.com/education/How-long-do-empires-last
If you assume that Earth’s technological civilization got started with the industrial revolution around the year 1800, then these estimates imply that our current civilization will fall around 2150. It would be quite ironic if the CO2 emissions caused by modern industry give us the same life span as ancient civilizations powered by water wheels and beasts of burden.
However, dating the industrial revolution to 1800 is rather arbitrary. Some people think it started around 1760 or even earlier. A more basic question is whether the average length of an ancient civilization is relevant to forecasting the length of a modern technological civilization. I suspect it is not.
To see why, let’s do a thought experiment to consider what might bring an end to Earth’s civilization.
Nuclear war? No, much of Earth’s southern hemisphere would survive and recover. (However, a world with a single Pangaea like continent might not be so lucky.)
A drug resistant pandemic? It would kill a lot of people, but like the Black Plague, immunity would eventually develop and civilization would recover. For areas that could enforce a quarantine, recovery would be even faster.
Global warming? Probably not. Even rapid climate change will leave some regions relatively well off. Think of Russia or Canada on Earth, (although they would both lose their coastal cities.)
Asteroid strike? Only if the civilization had no missile technology. This might occur on a planet with no moon to explore, but given the benefits of satellite technology, it’s likely even a moonless world will develop missiles.
Overpopulation? Our civilization on Earth has survived numerous famines and other consequences of overpopulation.
So it seems that once a worldwide technological civilization arises, it will last a very long time, perhaps 10,000 years or more. Others have suggested even a billion years. https://en.wikipedia.org/wiki/Drake_equation.
This conclusion that L is a very large number suggests that fc (the number of signal emitting civilizations in the galaxy) must be a low number. Otherwise we should have detected one of these long lived civilization by now. An exception though is the possibility that a technological civilization might choose to prioritize directional antennas or fiber optics. This would reduce the amount of broadcast signals emitted into space.
But unfortunately all this is just intelligent speculation. Earth is the only planet in the universe where we know there is life. As many have said, you really can’t tell anything from a sample size of one.
It also depends on your definition of civilization. Using the definition you use, it seems like there are lots of independent civilizations of short duration. (The “Third Reich” proved very short ). However, each civilization is not independent and their advances, both cultural and technological tend to accumulate. Our current “Western” civilization might well be eclipsed by an “Eastern” one, but it will continue technology development and probably economic growth.
So perhaps better to consider the arc of civilizational artifacts like technology as the relevant index. On that basis, we might well start our clock at the first building of cities (from the Latin, civitas, or ”city”) which makes civilization at least 10,000 years. Although there may well be setbacks again, I would be surprised if civilization disappeared anytime soon.
Religious fanatics capable bio-engineering are another potential risk. An engineered highly comtagious virus with delayed effect and detectability is a plausible doomsday event.
Two points:
First, any sort of organized civilization should be contacted. If you can see their works from orbit, go down and say hi. Otherwise you’re putting yourself in the position of judging whether or not they are “ready” — which is both incredibly arrogant and ridiculous. It’s ridiculous because of course nobody is ever going to be “ready” for first contact with another intelligent species, so we’re just projecting our own historical guilt, neuroses, and wishful thinking onto them.
Second, the discovery of an intelligent species in the Alpha Centauri system would be the most terrifying news ever. It means that intelligence is not rare — which in turn means that the fact that we haven’t been able to detect any spacefaring civilizations implies something really bad is about to happen to us.
ACEsat is an ingenious solution to a complex problem . Telescope stability, that is currently challenging direct imaging of exoplanets both for WFIRST and any future coronagraph based space ELT. The greater the precision / inner working angle and contrast of a coronagraph, the greater the telescope stability required. Down to as low as pico meters !( 1e12) even.
For space based telescopes this is managed by so called low and high order wavefront control , the space equivalent of adaptive optics . Tiny deformable mirrors ( MEMS) modify their shape according to instructions from an on board computer fed by a small sample of incoming light ,for low order correction which is so precise it still needs additional real time input from the ground . High order correction is managed by the on board computer too through control of a ” tip/tilt ” mirror and is somewhat easier but still demanding . All required in a tiny fractions of a second. Together they represent a nightmare for designers and observers ! The computing power alone is substantial for a space based processor .
The whole process is thrown out of kilter by the tiniest of movements whether they be due to vibration of the telescope itself ( perhaps due to an attitude thruster , a reaction wheel as on Kepler or even temperature related expansion / contraction in the mirror material ) . Just a sample of causes that need to be addressed ) . All of this needs to be mitigated and the bigger the telescope the more so .
Building the coronagraph into the telescope helps increase its stiffness and also allows it to be part of the telescopes optical train . The less mirrors in this , the less there is to vibrate . In general the nearer the coronagraph to the optical plane the better for stability too and using the coronagraph mirrors themselves as the first part of the telescope train is a highly ingenious way of doing this in smaller telescopes up to 1.5m .
Even the choice of construction material and telescope design is critical. “Off axis” telescopes ( with an angled primary mirror aimed at a secondary on the lip of the telescope baffle out of the plane of incoming light ) remove the central obstruction created by the secondary mirror and its suspending “spiders” in a conventional “on axis” telescopes . Apart from blocking up to 20% of light entering the scope this obstruction diffracts it too making any wavefront control even more duffucult.
Silicon carbide based mirrors ( Herschel space telescope , Gaia , LORRI on New Horizons and the NIRspec on JWST are prime examples ) have a very favourable CFE , coefficient of thermal expansion , which means it doesn’t alter shape much in response to temperature changes . It is also lightweight and strong allowing use as a construction material too. One material for nearly the whole telescope further increases stability whilst lowering costs .( the 3.5m Herschel mirror weighed just 250kgs versus 2.4m WFIRSTs 2000 kgs !). That said , the development of WFIRST-AFTA has been a welcome catalyst that has driven forward coronagraph technology by years nee decades just in the few years since its inception.
Earth trailing orbits maintain a very stable temperature which further favours precision imaging and that is why such an orbit was chosen for Kepler whose prolongued observation periods without movement help create further stability and are the basis for ACEsat’s two year Alpha Centauri mission, though a much bigger scope could manage on shorter times allowing additional targets to be investigated within reasonable timeframe.
The existence of an exoplanet telescope concept that can scale to 1.5m whilst overcoming all the stability issues described above and which could be launched within five years with a modest degree of development is simultaneously encouraging and disappointing . Despite a low cost unless it fits within the $250 million of a large Explorer mission, it won’t happen .
What could be more scientifically beneficial than characterising our neighbouring star system or in the case of the largest version of ACEsat , stars out as far as twenty light years or so . There are by my (optimistic ) reckoning atleast 8 stars capable of harbouring life of some type within twenty light years and a six year mission with a 1.5m telescope could compensate for its relatively small size with minimum ten month plus observation periods climbing as high up as two and a half years.
Current estimates suggest up to four planets per star ( not all habitable zone of course) , so that’s thirty plus planets characterised if the telescope has a low resolution spectroscope ( an integral field spectroscope ,IFS, whose multiple diffraction grids create a three dimensional spectrum that allows additional post processing of any image thus providing increased contrast on top of that provided by the coronagraph and accurate orbital mapping of any planets . The designers of ACEsat emphasise the importance of post processing in reducing the need for “raw” contrast from the coronagraph itself thus reducing strenous stability requirements .
ACEsat is a telescope a good decade ahead of its time. Just a 45 cm aperture can see habitable zone Earth sized or smaller planets around a star 250000 plus AU away ( the distance then sounds more impressive than 4.35 light years). Even the technological triumph that is 2.4m WFIRST isn’t expected to do that when it launches in 2024!
Thanks for that post.
It’s great to see just what can be achieved. The problem with exoplanet imaging is that without a very large aperture ( 10m plus ) it needs extended observation in order to get enough photons for an image and spectrographic characterisation .( another draw back of high precision coronagraphs is the limited bandwidth over which they can image -No more than a few hundreds of nano metres , with the otherwise impressive PIAA version one if the worst offenders ) .
But large apertures are currently impossible because of the stability issues described , though worldwide intensive research is being devoted to trying to resolve this. The ACEsat design cleverly bypasses all this by building the coronagraph into the telescope itself , both structurally but also reducing the optical train by direct incorporation of its mirror elements in to the train. The massively extended observation period of two years allows accurate construction of any planets’ orbits which allows a unique 1000 times plus increase in contrast post imaging , that is NOT provided by the coronagraph , which can be consequently reduced in precision thus lowering its demanding stability requirements . The whole telescope /coronagraph unit is devoted to maximum stability and maximum contrast both of which give a minimum inner working angle . Sadly this design only works up to about 1.5m after which incorporating bigger coronagraphs becomes impractical . But 1.5m is far from negligible ( as shown by the results of 0.45m) if enough time is devoted per target. This is only going to be possible with a dedicated telescope however , though the largest such version should over a six year mission ( similar to PLATO and Euclid so perfectly feasible for an uncomplicated design with enough “consumables” and a simple sensor array and passively cooled spectrograph ) can still deliver extensive and exciting science. And not expensive too.
The problem is that after massive Flagship general purpose telescopes the next biggest budget is a limited $250 million through the large Explorer programme . There is no astrophysics “Discovery” or “New Frontiers ” equivalent for exoplanets despite these being for planetary science. Just the sort of funding required for a mid sized exoplanet telescope like an ACEsat plus . Ironically it was Kepler’s amazing (and prolonged) success that led to a ban, yes an actual ban , on these programmes use for anything other than planetary science. Not that that has stopped dwarf planet , cometary and asteroid missions , with Trojan and Kuiper belt proposals as well .
Paul didn’t hear anything from the ACEsat team about a resubmission though their suggestion of a smaller , 0.3m version implies skepticism over it being delivered within budget . Another option would be to increase its size and aim for a large Explorer but to be successful here it would need to target more than one planetary system . Unfortunately Alpha Centauri is unique in possessing two “life friendly ” stars so close with nothing but difficult to image and faint M dwarfs till around a much more distant 11 light years , that would require a prohibitively expensive 1.5m telescope mission to image .
Nasa originally intended to have two Disvovery missions in a five year period , staggered to one per 2.5 years to avoid excessive operations costs and to always have something on the go . One could have been planetary , one astrophysics including exoplanets. So far budgetary constraints have stopped the two missions and an astrophysics component would need the entire disparate but burgeoning exoplanet community to unite behind an astrophysics mission and lobby en masse. They have done this to a degree already for a transit spectroscopy telescope though, and this is something to look out for early next year when the MIDEX 2021 shortlist is announced .
So there is hope . There is also a push to have a once in decade funded astrophysics Probe mission ( $1 billion plus government provided technology, a launch and operations – so a small flagship in all but name ) after the next Decadel which would certainly open the door to some very capable concepts .
“Civilization is an interlude between two ice ages””. A.C. Clarke
Some useful background information on the Alpha Centauri system:
http://earthsky.org/brightest-stars/alpha-centauri-is-the-nearest-bright-star