Could an advanced civilization create artificial black holes? If so, the possibilities for power generation and interstellar flight would be profound. Imagine cold worlds rendered habitable by tiny artificial ‘suns.’ Robert Zubrin, who has become a regular contributor to Centauri Dreams, considers the consequences of black hole engines in the essay below. Dr. Zubrin is an aerospace engineer and founder of the Mars Society, as well as being the president of Pioneer Astronautics. His latest book, The Case for Space: How the Revolution in Spaceflight Opens Up a Future of Limitless Possibility, was recently published by Prometheus Books. As Zubrin notes, generating energy through artificial singularities would leave a potential SETI signal whose detectability is analyzed here, a signature unlike any we’ve examined before.
by Robert Zubrin
Abstract
Artificial Singularity Power (ASP) engines generate energy through the evaporation of modest sized (108-1011 kg) black holes created through artificial means. This paper discusses the design and potential advantages of such systems for powering large space colonies, terraforming planets, and propelling starships. The possibility of detecting advanced extraterrestrial civilizations via the optical signature of ASP systems is examined. Speculation as to possible cosmological consequences of widespread employment of ASP engines is considered.
Introduction

According to a theory advanced by Stephen Hawking [1] in 1974, black holes evaporate at a rate given by:
tev = (5120π)tP(m/mP)3 (1)
where tev is the time it takes for the black hole to evaporate, tP is the Planck time (5.39e-44 s), m is the mass of the black hole in kilograms, and mP is the Planck mass (2.18e-8 kg) [2]
Hawking considered the case of black holes formed by the collapse of stars, which need to be at least ~3 solar masses to occur naturally. For such a black hole, equation 1 yields an evaporation time of 5e68 years, far longer than the expected life of the universe. In fact, evaporation would never happen, because the black hole would gain energy, and thus mass, by drawing in cosmic background radiation at a rate faster than its own insignificant rate of radiated power.
However it can be seen from examining equation (1) that the evaporation rate goes inversely with the cube of singularity, which means that the emitted power (=mc2/tev) goes inverse with the square of the mass. Thus if the singularity could be made small enough, very large amounts of power could theoretically be produced.
This possibility was quickly grasped by science fiction writers, and such propulsion systems were included by Arthur C. Clarke in his 1976 novel Imperial Earth [3] and Charles Sheffield in his 1978 short story “Killing Vector.” [4]
Such systems did not receive serious technical analysis however, until 2009, when it was examined by Louis Crane and Shawn Westmoreland, both then of Kansas State University, in their seminal paper “Are Black Hole Starships Possible?” [5]
In their paper, Crane and Westmoreland focused on the idea of using small artificial black holes powerful enough to drive a starship to interstellar-class velocities yet long-lived enough to last the voyage. They identified a “sweet spot” for such “Black Hole Starships” (BHS) with masses on the order of 2×109 kg, which they said would have lifetimes on order of 130 years, yet yield power of about 13,700 TW. They proposed to use some kind of parabolic reflector to reflect this radiation, resulting in a photon rocket. The ideal thrust T of a rocket with jet power P and exhaust velocity v is given by:
T = 2P/v (2)
So with T = 13,700 TW and v=c = 3e8 m/s, the thrust would be 8.6e7 N. Assuming that the payload spacecraft had a mass of 1e9 kg, this would accelerate the ship at a rate of a=8.6e7/3e9 = 2.8e-2 m/s2. Accelerating at this rate, such a ship would reach about 30% the speed of light in 100 years.
There are a number of problems with this scheme. In the first place, the claimed acceleration is on the low side. Furthermore their math appears to be incorrect. A 2e9 kg singularity would only generate about 270 TW, or 1/50th as much as their estimate, reducing thrust by a factor of 50 (although it would last about 20,000 years). These problems could be readily remedied, however, by using a smaller singularity and a smaller ship. For example a singularity with a mass of 2e8 kg would produce a power of 26,900 TW. Assuming a ship with a mass of 1e8 kg, an acceleration of 0.6 m/s2 could be achieved, allowing 60% the speed of light to be achieved in 10 years. The singularity would only have a lifetime of 21 years. However it could be maintained by being constantly fed mass at a rate of about 0.33 kg/s.
A bigger problem is that a 1e9 kg singularity would produce radiation with a characteristic temperature of 9 GeV, increasing in inverse proportion to the singularity mass. So for example a 1e8 kg singularity would produce gamma rays with energies of 90 GeV (i.e. for Temperature, T, in electron volts, T = 9e18/m.) There is no known way to reflect such high energy photons. So at this point the parabolic reflector required for the black hole starship photon engine is science fiction.
Yet another problem is the manufacture of the black hole. Crane and Westmoreland suggest that it could be done using converging gamma ray lasers. To make a 1e9 kg unit, they suggested a “high-efficiency square solar panel a few hundred km on each side, in a circular orbit about the sun at a distance of 1,000,000 km” to provide the necessary energy. A rough calculation indicates the implied power of this system from this specification is on the order of 106 TW, or about 100,000 times the current rate used by human civilization. As an alternative construction technique, they also suggest accelerating large masses to relativistic velocities and then colliding them. The density of these masses would be multiplied both by relativistic mass increase and length contraction. However the energy required to do this would still equal the combined masses times the speed of light squared. While this technique would eliminate the need for giant gamma ray lasers, the same huge power requirement would still present itself.
In what follows, we will examine possible solutions for the above identified problems.
Advanced Singularity Engines
In MKS units, equation (1) can be rewritten as:
tev = 8.37e-15 m3 (3)
This implies that the power, P, in Watts, emitted by the singularity is given by:
P = 1.08e33/m2 (4)
The results of these two equations are shown in Fig. 1.
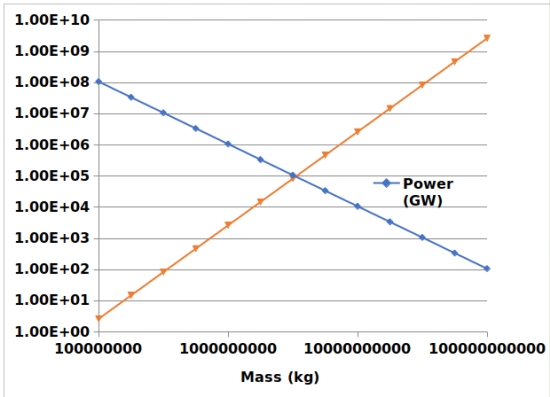
Fig 1. Power and Lifetime of ASP Engines as a Function of Singularity Mass
No credible concept is available to enable a lightweight parabolic reflector of the sort needed to enable the Black Hole Starship. But we can propose a powerful and potentially very useful system by dropping the requirement for starship-relevant thrust to weight ratios. Instead let us consider the use of ASP engines to create an artificial sun.
Consider a 1e8 kg ASP engine. As shown in Fig 1, it would produce a power of 1.08e8 Gigawatts. Such an engine, if left along, would only have a lifetime of 2.65 years, but it could be maintained by a constant feed of about 3 kg/s of mass. We can’t reflect its radiation, but we can absorb it with a sufficiently thick material screen. So let’s surround it with a spherical shell of graphite with a radius of 40 km and a thickness of 1.5 m. At a distance of 40 km, the intensity of the radiation will be about 5 MW/m2, which the graphite sphere can radiate into space with a black body temperature of 3000 K. This is about the same temperature as the surface of a type M red dwarf star. We estimate that graphite has an attenuation length for high energy gamma rays of about 15 cm, so that 1.5 m of graphite (equivalent shielding to 5 m of water or half the Earth’s atmosphere) will attenuate the gamma radiation by ten factors of e, or 20,000. The light will then radiate out further, dropping in intensity with the square of the distance, reaching typical Earth sunlight intensities of 1 kW/m2 at a distance of about 3000 km from the center.
The mass of the artificial star will be about 1014 kg (that’s the mass of the graphite shell, compared to which the singularity is insignificant.). As large as this is, however, it is still tiny compared to that of a planet, or even the Earth’s Moon (which is 7.35e22 kg). So, no planet would orbit such a little star. Instead, if we wanted to terraform a cold world, we would put the mini-star in orbit around it.
The preferable orbital altitude of the ASP mini-star of 3000 km altitude in the above cited example was dictated by the power level of the singularity. Such a unit would be sufficient to provide all the light and heat necessary to terraform an otherwise sunless planet the size of Mars. Lower power units incorporating larger singularities but much smaller graphite shells are also feasible. (Shell mass is proportional to system power.) These are illustrated in Table 1.
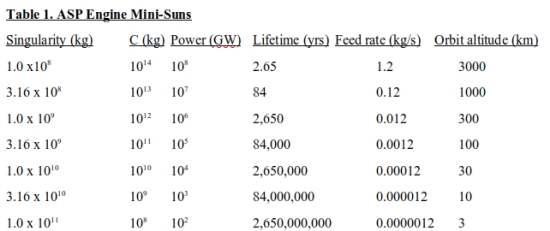
The high-powered units listed in Table 1 with singularity masses in the 1e8 to 1e9 kg range are suitable to serve as mini-suns orbiting planets, moons or asteroids, with the characteristic radius of such terraforming candidates being about the same as the indicated orbital altitude. The larger units, with lower power and singularity masses above 1e10 kg are more appropriate for space colonies.
Consider an ASP mini-sun with a singularity mass of 3.16e10 kg positioned in the center of a cylinder with a radius of 10 km and a length of 20 km. The cylinder is rotating at a rate of 0.0316 radians per second, which provides it with 1 g or artificial gravity. Let’s say the cylinder is made of material with an areal density of 1000 kg per square meter. In this case it will experience an outward pressure of 104 pascals, or about 1.47 psi, due to outward acceleration. If the cylinder were made of solid Kevlar (density = 1000 kg/m3) it would be about 1 m thick. So the hoop stress on it would be 1.47*(10,000)/1 = 14,700 psi, which is less than a tenth the yield stress of Kevlar. Or put another way, 10 cm of Kevlar would do the job of carrying the hoop stress, and the rest of mass load could be anything, including habitations. If the whole interior of the cylinder were covered with photovoltaic panels with an efficiency of 10 percent, 100 GWe of power would be available for use of the inhabitants of the space colony, which would have an area of 1,256 square kilometers. The mini-sun powering it would have a lifetime of 84 million years, without refueling. Much larger space colonies (i.e, with radii over ~100 km) would not be possible however, unless stronger materials become available, as the hoop stress would become too great.
Both of these approaches seem potentially viable in principle. However we note that the space colony approach cited requires a singularity some 300 times more massive than the approach of putting a 1e8 kg mini-sun in orbit around a planet, which yields 4π(3000)2 = 100 million square kilometers of habitable area, or about 80,000 times as much land. Furthermore, the planet comes with vast supplies of matter of every type, whereas the space colony needs to import everything.
Building Singularities
Reducing the size of the required singularity by a factor of 10 from 1e9 to 1e8 kg improves feasibility of the ASP concept somewhat, but we need to do much better. Fortunately there is a way to do so.
If we examine equation (3), we can see that the expected lifetime of a 1000 kg singularity would be about 8.37 x 10-6 s. In this amount of time, light can travel about 250 m. and an object traveling at half the speed of light 125 m. If a sphere with a radius of 125 m were filled with steel it would contain about 8 x 1010 kg, or about 100 times what we need for our 1e8 kg ASP singularity. In fact, it turns out that if the initial singularity is as small as about 200 kg, and fired into a mass of steel, it will gain mass much faster than it losses it, and eventually grow into a singularity as massive as the steel provided.
By using this technique we can reduce the amount of energy required to form the required singularity by about 7 orders of magnitude compared to Crane and Westmoreland’s estimate. So instead of needing a 106 TW system, a 100 GW gamma ray laser array might do the trick. Alternatively, accelerating two 200 kg masses to near light speed would require 3.6e7 TJ, or 10,000 TW-hours of energy. This is about the energy humanity currently uses in 20 days. We still don’t know how to do it, but reducing the scale of the required operation by a factor of 10 million certainly helps.
ASP Starships
We now return to the subject of ASP starships. In the absence of a gamma ray reflector, we are left with using solid material to absorb the gamma rays and other energetic particles and re-radiate their energy as heat. (Using magnetic fields to try to contain and reflect GeV-class charged particles that form a portion of the Hawking radiation won’t work because the required fields would be too strong and too extensive, and the magnets to generate them would be exposed to massive heating by gamma radiation.)
Fortunately, we don’t need to absorb all the radiation in the absorber/reflector, we only need to absorb enough to get it hot. So let’s say that we position a graphite hemispherical screen to one side of a 1e8 kg ASP singularity, but instead of making it 1.5 m thick, we make it 0.75 mm thick. At that thickness it will only absorb about 5 percent of the radiation that hits it, the rest will pass right through. So we have 5e6 GW of useful energy, which we want to reduce to 5 MW/m2 in order for the graphite to be kept at ~3000 K where it can survive. The radius will be about 9 km, and the mass of the graphite hemisphere will be about 6e8 kg. A thin solar sail like parabolic reflector with an area 50 times as great and the carbon hemisphere but a thickness 1/500th (i.e. 1.5 microns) as great would be positioned in front of the hemisphere, adding another 0.6 e8 kg to the system, which then plus the singularity and the 1e8 kg ship might be 7.6e8 kg in all. Thrust will be 0.67e8 N, so the ship would accelerate at a speed of 0.67/7.6 = 0.09 m/s2, allowing it to reach 10 percent the speed of light in about 11 years.
Going much faster would become increasingly difficult, because using only 5% of the energy of the singularity mass would give the system an effective exhaust velocity of about 0.22 c. Higher efficiencies might be possible if a significant fraction of the Hawking radiation came off as charged particles, allowing a thin thermal screen to capture a larger fraction of the total available energy. In this case, effective exhaust velocity would go as c times the square root of the achieved energy efficiency. But sticking with our 5% efficiency, if we wanted to reach 0.22 c we could, but we would require a mass ratio of 2.7, meaning we would need about 1.5e9 kg of propellant to feed into the ASP engine, whose mass would decrease our average acceleration by about a factor of two over the burn, meaning we would take about 40 years to reach 20 percent the speed of light.
Detecting ET
The above analysis suggests that if ASP technology is possible, using it to terraform cold planets with orbital mini-suns will be the preferred approach. Orbiting (possibly isolated) cold worlds at distances of thousands of kilometers, and possessing 3000 K type M red dwarf star spectra, potentially with gamma radiation in excess of normal stellar expectations, it is possible that such objects could be detectable.
Indeed, one of the primary reasons to speculate on the design of ASP engines right now is to try to identify their likely signature. We are far away from being able to build such things. But the human race is only a few hundred thousand years old, and human civilization is just a few thousand years. In 1905 the revolutionary HMS Dreadnought was launched, displacing 18,000 tons. Today ships 5 times that size are common. So it is hardly unthinkable that in a century or two we will have spacecraft in the million ton (109 kg) class. Advanced extraterrestrial civilizations may have reached our current technological level millions or even billions of years ago. So they have had plenty of time to develop every conceivable technology. If we can think it, they can build it, and if doing so would offer them major advantages, they probably have. Thus, looking for large energetic artifacts such as Dyson Spheres [6], starships [7,8], or terraformed planets [9] is potentially a promising way to carry out the SETI search, as unlike radio SETI, it requires no mutual understanding of communication conventions. Given the capabilities the ASP technology would offer any species seeking to expand it prospects by illuminating and terraforming numerous new worlds, such systems may actually be quite common.
ASP starships are also feasible and might be detectable as well. However the durations of starship flights would be measured in decades or centuries, while terraformed worlds could be perpetual. Furthermore, once settled, trade between solar systems could much more readily be accomplished by the exchange of intellectual property via radio than by physical transport. As a result, the amount of flight traffic will be limited. In addition, there could be opportunities for employment of many ASP terraforming engines within a single solar system. For example, within our own solar system there are seven worlds of planetary size (Mars, Ceres, Ganymede, Calisto, Titan, Triton, and Pluto) whose terraforming could be enhanced or enabled by ASP systems, not to mention hundreds of smaller but still considerable moons and asteroids, and potentially thousands of artificial space colonies as well. Therefore the number of ASP terraforming engines in operation in the universe at any one time most likely far exceeds those being used for starship propulsion. It would therefore appear advantageous to focus the ASP SETI search effort on such systems.
Proxima Centauri is a type M red dwarf with a surface temperature of 3000 K. It therefore has a black body spectrum similar to that of the 3000 K graphite shell of our proposed ASP mini-sun discussed above. The difference however is that it has about 1 million times the power, so that an ASP engine placed 4.2 light years (Proxima Centauri’s distance) from Earth would have the visual brightness as a star like Proxima Centauri positioned 4,200 light years away. Put another way, Proxima Centauri has a visual magnitude of 11. It takes 5 magnitudes to equal a 100 fold drop in power, so our ASP engine would have a visual magnitude of 26 at 4.2 light years, and magnitude 31 at 42 light years. The limit of optical detection of the Hubble Space Telescope is magnitude 31. So HST would be able to see our proposed ASP engine out to a distance of about 50 light years, within which there are some 1,500 stellar systems.
Consequently ASP engines may already have been imaged by Hubble, appearing on photographs as unremarkable dim objects assumed to be far away. These should be subjected to study to see if any of them exhibit parallax. If they do, this would show that they are actually nearby objects of much lower power than stars. Further evidence of artificial origin could be provided if they were found to exhibit a periodic Doppler shift, as would occur if they were in orbit around a planetary body. An anomalous gamma ray signature could be present as well.
I suggest we have a look.
Cosmological Implications
One of the great mysteries of science is why the laws of the universe are so friendly to life. Indeed, it can be readily shown that if any one of most of the twenty or so apparently arbitrary fundamental constants of nature differed from their actual value by even a small amount, life would be impossible [9]. Some have attempted to answer this conundrum by claiming that there is nothing to be explained because there are an infinite number of universes; we just happen to live in the odd one where life is possible. This multiverse theory answer is absurd, as it could just as well be used to avoid explaining anything. For example take the questions, why did the Titanic sink/it snow heavily last winter/the sun rise this morning/the moon form/the chicken cross the road? These can all also be answered by saying “no reason, it other universes they didn’t.” The Anthropic Principle reply, to the effect of “clearly they had to, or you wouldn’t be asking the question” is equally useless.
Clearly a better explanation is required. One attempt at such an actual causal theory was put forth circa 1992 by physicist Lee Smolin [10], who says that daughter universes are formed by black holes created within mother universes. This has a ring of truth to it, because a universe, like a black hole, is something that you can’t leave. Well, says Smolin, in that case, since black holes are formed from collapsed stars, the universes that have the most stars will have the most progeny. So to have progeny a universe must have physical laws that allow for the creation of stars. This would narrow the permissible range of the fundamental constants by quite a bit. Furthermore, let’s say that daughter universes have physical laws that are close to, but slightly varied from that of their mother universes. In that case, a kind of statistical natural selection would occur, overwhelmingly favoring the prevalence of star-friendly physical laws as one generation of universes follows another.
But the laws of the universe don’t merely favor stars, they favor life, which certainly requires stars, but also planets, water, organic and redox chemistry, and a whole lot more. Smolin’s theory gets us physical laws friendly to stars. How do we get to life?
Reviewing an early draft of Smolin’s book in 1994, Crane offered the suggestion [11] that if advanced civilizations make black holes, they also make universes, and therefore universes that create advanced civilizations would have much more progeny than those that merely make stars. Thus the black hole origin theory would explain why the laws of the universe are not only friendly to life, but the development of intelligence and advanced technology as well. Universes creates life because life creates universes. This result is consistent with complexity theory, which holds that if A is necessary to B, then B has a role in causing A.
These are very interesting speculations. So let us ask, what would we see if our universe was created as a Smolin black hole, and how might we differentiate between a natural star collapse or ASP engine origin? From the above discussion, it should be clear that if someone created an ASP engine, it would be advantageous for them to initially create a small singularity, then grow it to its design size by adding mass at a faster rate than it evaporates, and then, once it reaches its design size, maintain it by continuing to add mass at a constant rate equal to the evaporation rate. In contrast, if it were formed via the natural collapse of a star it would start out with a given amount of mass that would remain fixed thereafter.
So let’s say our universe is, as Smolin says, a black hole. Available astronomical observations show that it is expanding, at a velocity that appears to be close to the speed of light. Certainly the observable universe is expanding at the speed of light.
Now a black hole has an escape velocity equal to the speed of light. So for such a universe
c2/2 = GM/R (5)
Where G is the universal gravitational constant, c is the speed of light in vacuum, M is the mass of the universe, and R is the radius of the universe.
If we assume that G and c are constant, R is expanding at the speed of light, and τ is the age of the universe, then:
R = cτ (6)
Combining (5) and (6), we have.
M/τ = (Rc2/2G)(c/R) = c3/2G (7)
This implies that the mass of such a universe would be growing at a constant rate. Contrary to the classic Hoyle continuous creation theory, however, which postulated that mass creation would lead to a steady state universe featuring constant density for all eternity, this universe would have a big bang event with density decreasing afterwards inversely with the square of time.
Now the Planck mass, mp, is given by:
mp = (hc/2πG)½ (8)
And the Planck time, tp, is given by:
tp = (hG/2πc5)½ (9)
If we divide equation (8) by equation (9) we find:
mp/tp = c3/G (10)
If we compare equation (10) to equation (7) we see that:
M/τ = ½(mp/tp) (11)
So the rate at which the mass of such a universe would increase equals exactly ½ Planck mass per Planck time.
Comparison with Observational Astronomy
In MKS units, G = 6.674e-11, c= 3e+8, so:
M/τ= c3/2G = 2.02277 e+35 kg/s. (12)
For comparison, the mass of the Sun is 1.989+30 kg. So this is saying that the mass of the universe would be increasing at a rate of about 100,000 Suns per second.
Our universe is believed to be about 13 billion years, or 4e+17 seconds old. The Milky Way galaxy has a mass of about 1 trillion Suns. So this is saying that the mass of the universe should be about 40 billion Milky Way galaxies. Astronomers estimate that there are 100 to 200 billion galaxies, but most are smaller than the Milky Way. So this number is in general agreement with what we see.
According to this estimate, the total mass of the universe M, is given by:
M = (2e+35)(4e+17) = 8e+52 kg. (13)
This number is well known. It is the critical mass required to make our universe “flat.” It should be clear, however, that when the universe was half as old, with half its current diameter, this number would have needed to be half as great. Therefore, if the criteria is that such a universe mass always be critical for flatness, and not just critical right now, then its mass must be increasing linearly with time.
These are very curious results. Black holes, the expanding universe, and the constancy of the speed of light are results of relativity theory. Planck masses and Planck times relate to quantum mechanics. Observational astronomy provides data from telescopes. It is striking that these three separate approaches to knowledge should provide convergent results.
This analysis does require that mass be continually added to the universe at a constant rate, exactly as would occur in the case of an ASP engine during steady-state operation. It differs however in that in an ASP engine, the total mass only increases during the singularity’s buildup period. During steady state operation mass addition would be balanced by mass evaporation. How these processes would appear to the inhabitants of an ASP universe is unclear. Also unclear is how the inhabitants of any Smolinian black hole universe could perceive it as rapidly expanding. Perhaps the distance, mass, time, and other metrics inside a black hole universe could be very different from those of its parent universe, allowing it to appear vast and expanding to its inhabitants while looking small and finite to outside observers. One possibility is that space inside a black hole is transformed, in a three dimensional manner analogous to a ω = 1/z transformation in the complex plane, so that the point at the center becomes a sphere at infinity. In this case mass coming into the singularity universe from its perimeter would appear to the singularity’s inhabitants as matter/energy radiating outward from its center.
Is there a model that can reconcile all the observations of modern astronomy with those that would be obtained by observers inside either a natural black hole or ASP universe? Speculation on this matter by scientists and science fiction writers with the required physics background would be welcome [13].
Conclusions
We find that ASP engines appear to be theoretically possible, and could offer great benefits to advanced spacefaring civilizations. Particularly interesting is their potential use as artificial suns to enable terraforming of unlimited numbers of cold worlds. ASP engines could also be used to enable interstellar colonization missions. However the number of ASP terraforming engines in operation in the universe at any one time most likely far exceeds those being used for starship propulsion. Such engines would have optical signatures similar to M-dwarfs, but would differ in that they would be much smaller in power than any natural M star, and hence have to be much closer to exhibit the same apparent luminosity. In addition they would move in orbit around a planetary body, thereby displaying a periodic Doppler shift, and could have an anomalous additional gamma ray component to their spectra. An ASP engine of the type discussed would be detectable by the Hubble Space Telescope at distances as much as 50 light years, within which there are approximately 1,500 stellar systems. Their images may therefore already be present in libraries of telescopic images as unremarkable dim objects, whose artificial nature would be indicated if they were found to display parallax. It is therefore recommended that such a study be implemented.
As for cosmological implications, the combination of the attractiveness of ASP engines with Smolinian natural selection theory does provide a potential causal mechanism that could explain the fine tuning of the universe for life. Whether our own universe could have been created in such a manner remains a subject for further investigation.
References
1. Hawking, S. W. (1974). “Black hole explosions?” Nature 248(5443): 30-31. https://ui.adsabs.harvard.edu/abs/1974Natur.248…30H/abstract
2. Hawking Radiation, Wikipedia https://en.wikipedia.org/wiki/Hawking_radiation accessed September 22, 2019.
3. Arthur C. Clarke, Imperial Earth, Harcourt Brace and Jovanovich, New York, 1976.
4. Charles Sheffield, “Killing Vector,” in Galaxy, March 1978.
5. Louis Crane and Shawn Westmoreland, “Are Black Hole Starships Possible?” 2009, 2019. https://arxiv.org/pdf/0908.1803.pdf accessed September 24.
6. Freeman Dyson, “The Search for Extraterrestrial Technology,” in Selected Papers of Freeman Dyson with Commentary, Providence, American Mathematical Society. Pp. 557-571, 1996.
7. Robert Zubrin, “Detection of Extraterrestrial Civilizations via the Spectral Signature of Advanced Interstellar Spacecraft,” in Progress in the Search for Extraterrestrial Life: Proceedings of the 1993 Bioastronomy Symposium, Santa Cruz, CA, August 16-20 1993.
8. Crane, “Searching for Extraterrestrial Civilizations Using Gamma Ray Telescopes,” available at https://arxiv.org/abs/1902.09985.
9. Robert Zubrin, The Case for Space: How the Revolution in Spaceflight Opens Up a Future of Limitless Possibility, Prometheus Books, Amherst, NY, 2019.
10. Paul Davies, The Accidental Universe, Cambridge University Press, Cambridge, 1982
11. Lee Smolin, The Life of the Cosmos, Oxford University Press, NY, 1997.
12. Louis Crane, “Possible Implications of the Quantum Theory of Gravity: An Introduction to the Meduso-Anthropic principle,” 1994. https://arxiv.org/PS_cache/hep-th/pdf/9402/9402104v1.pdf
13. I provided a light hearted explanation in my science fiction satire The Holy Land (Polaris Books, 2003) where the advanced extraterrestrial priestess (3rd Class) Aurora mocks the theory of the expanding universe held by the Earthling Hamilton. “Don’t be ridiculous. The universe isn’t expanding. That’s obviously physically impossible. It only appears to be expanding because everything in it is shrinking. What silly ideas you Earthlings have.” In a more serious vein, the late physicist Robert Forward worked out what life might be like on a neutron star in his extraordinary novel Dragon’s Egg (Ballantine Books, 1980.) A similar effort to describe life on the inside of a black hole universe could be well worthwhile. Any takers?
Robert Zubrin
Pioneer Astronautics
11111 W. 8th Ave, unit A
Lakewood, CO 80215
Zubrin@aol.com



We may already have one–I hope:
https://arxiv.org/pdf/1909.11090.pdf
Bob, I respect you–but the next time you talk to a non-space crowd–talk about this man, instead of Columbus:
https://www.britannica.com/biography/Zheng-He
China burned his treasure fleet, and built walls instead. You have to sweet talk the left on space:
https://www.space.com/patrick-stewart-billy-dee-williams-space-misconceptions-nycc.html
More importantly–SLS was the closest thing to your version of Ares–and instead of being thankful–you join the newspace mob in putting it and the people behind it under the bus.
Even Musk supports NTR:
https://mobygeek.com/features/elon-musk-proposes-using-nuclear-rockets-to-speed-up-mars-missions-7272
And LH2–which SLS has and Starship doesn’t– has the best specific impulse.
A good first mission for an NTR heavy probe would be to see if “plante 9” really is a black hole than can be used.
–publiusr
Shouldn’t we find out if Planet 9/X/Whatever actually exists first?
I know Columbus is not PC any more, but he and the vast majority of those Europeans who first came to the New World were seeking fortunes and land, which is how we are going to expand into space and gain a permanent foothold. Pure science has not been enough, and governments are too fickle when it comes to permanent space settlement and utilization.
On the bright side, there will be a lot more science and no natives to mistreat in the Sol system compared to what happened in North and South America back in the day.
With respect Jeff I don’t think it’s a case of throwing SLS or the people behind it under the bus. It’s a case of getting the greatest payload per taxpayer (or in the case of private industry shareholder) dollar spent. If SLS is going to cost 1 to 1.5 billion dollars per launch and SpaceX is putting something like half the payload in orbit for 10 times less money then which is the better system? I’m really not sure what NASA should do about SLS and Orion and all the rest of it but it definitely isn’t a cost effective way to go into space. I would hope NASA can develop much more cost effective launch platforms in the future or they simply won’t be able to compete.
SLS uses hydrogen–and Musk won’t–at least for the time being.
I think Bezos needs to bring old and new Space together–and have Musk’s next-gen 19 meter super-heavy use SRBs and a whole SLS as an upper stage. THAT should be New Armstrong.
ANOTHER brand new way to detect advanced civilizations! “On the interstellar Von Neumann micro self-replicating probes.” by Z Ozmonov. ABSTRACT: “In this paper we consider efficiency of self-replicating extraterrestrial Von Neumann micro-scale robots and analyse the observational characteristics. By examining the natural scenario of moving in the HII clouds, it has been found that the timescale of replication might be several years and even less – making the process of observation quite promising. We have shown that by encountering the interstellar photons the probes might be visible at least in the infra-red energy band and the corresponding luminosities might reach tremendous values.” BIG QUESTION: Assuming that this is a rare process(otherwise, why haven’t we ALREADY detected this in nearby[astronomically speaking]H2 clouds),could the “enormous values” be detected in very far away H2 clouds with CURRENT technology, or will we have to wait for JWST? The only downside I see is that if the overall process takes several years, assuming a geometric progression followed by a complete shutdown of the entire process, observing the “enormous values” bay require an observation time of only days. Seems to me that we would have to be VERY VERY LUCKY to observe these “enormous values” in the very final stage of progress.
If this IS happening somewhere in the Milky Way galaxy, it could have HUGE implications for the origin of `Oumuamua! Now that the derelict lightsail theory put forward by Bialy and Loeb has been thoroughly discredited as a result of its low albedo AND its tumbling motion TOGETHER rendering it FAR TOO INEFFICIENT to be responsible for the observed non-gravitational acceleration, the ONLY lightsail mechanism that would work is my own RETRACTIBLE lightsail that is MISLEADING us into thinking that it is tumbling. The HUGE problem is that this scenario is CONTRIVED to explain EVERYTHING that all of the other NATURAL models CANNOT do! Enter “The interstellar object `Oumuamua as a fractal dust aggregate.” by Flekky E., Luu J., Toussaint R. This new paper itself is an aggregate derived from TWO PREVIOUS PAPERS! Zdenek Sekanina proposed that `Oumuamua is the dusty(i.e. ABSOLUTELY NO GAS)remanant of a large comet that broke apart close to perihelion passage, and Amaya Moro-Martin proposed that `Oumuamua is a fractal ICY aggregate that formed in the following way: “…porous aggregates can naturally aries from the collisional grows of ice particles beyond the snow line of a protoplanetary disk.” The former proposal has major problems dealing with the lack of meteor showers during `Oumuamua’s closest passage to Earth, while the latter proposal has major problems with ivevitable partial melting(resulting in contracton to the point of its becoming TOO INEFICIENT to explain the observed non-gravitational acceleration)or sublimation(resulting in a coma and gas tail, which was NOT observed)during periastron passage due to the accumulation of red dust over the eons which would absorb ENOUGH solar radiation to make such melting or sublimation INEVITABLE! This new proposal eliminates ALL of these problems, and in addition, explains the recently discovered(from the old data)SLOWDOWN in `Oumuamua’s ROTATION(allowing it to escape the fate proposed by Roman Rafikov that it would be torn apart due to an INCREASE in rotation as a result of the non-gravitational acceleration)due to YORP and Yankovsky effects! So now we have a NATURAL solution that COVERS ALL OF TE BASES, except for one(in my opinion – correct me if I am wrong)which is: How could such a thing form? The BASIS for an icy fractal aggregate forming from collisional grows is that when two icy particles collide, they partially MELT, leaving a RIGID aggregate. Dust collisions resulting in aggregates are thought to arise from electrostatic attraction(remember the famous ISS experiment) but can form rigid structures ONLY if they agglomerate in THREE DIMENSIONS(i.e., they CANNOT form SHEETS). So we have a PERFECT SOLUTION for `Oumuamua that CANNOT FORM NATURALLY! Enter nanobots! `Oumuamua origianally formed in a H2 cloud, and DELIBERATELY HEADED HERE! No “billions of years” travel timeline to degrade it. No other viable explanation as of the moment. And, to top it all off, in all likelihood, due to the close passage to Earth, WE HAVE BEEN SEEDED!!!!!
Seeded with nanobots? Why?
The interstellar object ‘Oumuamua as a fractal dust aggregate:
https://arxiv.org/abs/1910.07135
THIS is the paper everyone should be paying attention to:
Modeling the light curve of `Oumuamua: evidence for torque and disc-like shape:
https://arxiv.org/abs/1906.03696
Maybe and maybe not. Even though this paper adds “torque” to more efficiently explain the lightcurve data, and also preserve the object through the non-gravitational lightcurve phase by countering the Rafikov spin-up conundrum, it can ONLY spin DOWN the object via YORP and Yankovsky effects in the SHORT DURATION of the observations if the proposed disk were EXCEEDINGLY THIN, which brings us right back to lightsails again. ALSO: Another problem with the NATURAL fractal dust aggregate model is the ABRUPT CESSATION of non-gravitational acceleration as opposed to a more gradual one based on ONLY distance increase from the SUN. If you remember, this is EXACTLY what lead Micelli and Meech to reject the lack of data regarding outgassing and declare that `Oumuamua HAD to be a comet and HAD to have outgassed until it was too far from the Sun to continue doing so, leading to a VERY ABRUPT SHUTOFF of the outgassing and a corresponding abrupt cessation of the non-gravitational acceleration. Finally, I am not DEFINITATIVELY STATING OUTRIGHT that `Oumuamua IS composed of nanobots(two things MUST happen before I do that: ONE – Ozmanov’s claim MUST BE CONFIRMED BY OTHER THEORISTS, and TWO: My claim that a DUSTY fractal aggregate can ONLY form by NON-NATURAL means is not challenged by planetary formation theorists with much more knowledge in this field than I do. However. if everything I mentioned above AND Osmanov’s claim BOTH pass muster, `Oumuamua would not pass up on an opportunity to observe us VERY CLOSELY. Perhaps “seeding” was an inappropriate term, and leaving nanolurkers behind is a better way to explain it. Should this be the case, then the Moon would be an even better target than Earth, due to lack of an atmosphere, and thus no entry burnup issues.
ArXiv:1910.10303. “New Insights into Interstellar Object 1I/2017 U1(`Oumuamua)from SOHO/STERIO Nondetections.” by Man-To Hui, Matthew Matthew M. Knight. KEY QUOTE from the abstract: To exhibit the reported nongravitational motion…requires a nucleus bulk density of </~40 kg/m3." This is roughly 100 pounds per cubic meter as opposed to the 1/2 to 1 tonne per cubic meter of CNEOS 2014-01-08. this implies that `Oumuamua is VERY POROUS, but MUCH DENSER than a fractal aggregate of either dust or ice.
The ASP idea is impracticable for several reasons. I won’t deny that I am putting all my hopes in FTL technology, so I am biased against the ASP idea since at best it can produce relativistic propulsion. It takes a lot of energy to make a man made black hole. How it is made is not explained. We can’t just combine a lot of matter together since it always takes 3 solar masses to make a black hole that way because smaller black holes are not found in nature do to the Chandrasekar limit. With matter there is no designer Schwarzschild radius which is only a mathematical foundation or abstract mental exercise on paper which must be limited to the Chandrasekar limit in physical reality. It would take a lot of energy to crush or compress a small body beyond the Schwarzschild radius of a small body, and only gravitational energy of a large black hole of 3 solar masses can do that, i.e., we can’t take a smaller black hole out of 3 solar mass black hole since it would no longer be a black hole since it would be less than black hole energy and mass.. Maybe there might be particle collisions of cosmic rays which are close to the energy of particles inside black holes which last a very small fraction of a second. Consequently, the idea of black hole lifetimes of artificial or made black holes is superfluous and non sequitur.
In theory a smaller black hole could be man made, but it would take a lot of energy, specifically gravitational energy to make an man made or artificial black hole which could only be made and controlled using energy, not matter.
We couldn’t make a black hole by using lasers since they would not have enough gravitational energy. The gravitational energy of high energy photons is not enough. To make a man made black hole, we would need to be able to make very strong gravity waves through some kind of energy conversion of one of the other forces like electromagnetism into gravity, and we don’t know how to do that. We also would not need the energy of a small black hole to make a relativistic gravitational wave rocket. From what I recall reading is the radiation and gravity of the black hole might be too strong if it was near the spacecraft. How long would we even produce that much energy? https://en.wikipedia.org/wiki/Black_hole_starship
I don’t think our universe is inside a singularity or black hole. We would be crushed as a result. The singularity of the big bang is long gone after the explosion according to the big bang (Lambda CDM model). If the universe was shrinking, then how do we explain the cosmic redshift. Also dark energy is supposedly causing the expansion of our universe with a repulsive force which is the opposite of gravity and black holes.
The surface of a newton star is mostly electrons due the centrifugal force of the spinning. The inside of a neutron star is all Neutrons because the gravity is so strong, the electrons and protons have been combined and compressed into neutrons. A person standing on a neutron star would be squashed into electrons and neutrons. I was going to say squashed to atoms, but a person would not even be atoms. Time moves thirty percent slower on the surface of a neutrons star due to the strong gravity.
Hi Geoffrey,
You said:
There’s no magical crushing force inside an event horizon and a black hole big enough to be our visible Universe has a teeny tiny surface gravity. But to form in the first place, the Hole would need to have been White, to cause the expansion.
But that doesn’t stop Black Hole cosmology from being possible. It might mean the Black Hole is in more than just 3 space and one time dimension. It might need to be 5 dimensional.
regards,
Adam
There is so much that is so wrong about the above screed that I don’t know where to start and certainly don’t want to address all the points, so I’ll stick to the well-understood physics: the nature of the surface layers of a neutron star, working from the outside inwards.
First you come to the atmosphere. Everything we know about atomic physics and chemistry tells us that the layer will be gaseous and a few centimetres to a few metres thick. The height is somewhat arbitrary because it depends on where you set the limiting gas pressure. Compare the arbitrary 100km height of the top of the earth’s atmosphere.
Then you come to the crust. Radio observations of pulsars provide convincing evidence to back up the atomic and nuclear physics which suggest that it is a fairly rigid solid. That same physics tells us that discrete atomic nuclei are bound in a crystalline lattice by a sea of degenerate electrons. This is not so unfamiliar — much could be said about metals here on earth, the major difference is that in a neutron star crust all the electrons are in the sea and not just the valence electrons. A person would be squashed to nuclei and atoms. Your statement is just plain wrong: a person is electrically neutral; a collection of electrons and neutrons has a negative electric charge. Ever heard of the law of conservation of electric charge? We have absolutely no evidence whatsoever that it is ever violated.
The statement “The surface of a newton star is mostly electrons due the centrifugal force of the spinning.” completely ignores the fact that the electromagnetic interaction between positive nuclei and negative electrons is forty orders of magnitude greater than their gravitational interaction.
Going downwards, the pressure increases and electrons are increasingly likely to inverse-beta decay with atomic nuclei. The nuclei become more neutron-rich but are still relatively isolated from their neighbours; the crust is still a crystalline solid. Incidentally, the neutrinos produced in this reaction carry off some of the energy of the star.
Eventually, the nuclei become so neutron rich that they emit free neutrons (they can’t beta decay because the electron sea inhibits the reaction). The neutrons, being electrically neutral, can and do flow downwards under gravity. The composition of the star becomes ever more rich in free neutrons with a consequent ever smaller concentration of nuclei and their attendant electrons.
The detailed behaviour of compressed neutrons is not well understood. There is very good reason to think that at the pressures existing towards the center of a neutron star it exists as a super-fluid liquid.
Would it not be more efficient, to have the Habitation portion of the
Black hole Starship, be separated by 4 or 5 Km from the “Engine Room” and then add some shielding. After all, the acceleration is only about 1/16th of Earth Gravity. A network of structural beams could stay taught and firm at that acceleration, no neutron activation to worry about, at least at the back end of the ship.
I can only envision a SFC, building such a ship after evolving their technology to a point where the infrastructure and Energy required for Singularity Powered Ships is more efficient than Matter/Antimatter drive in both fueling and flight usage.
A SFC transitioning from KII to KIII is a likely candidate for this concept.
Having a 3000 K artificial sun would be great for us, warm blooded animals, but what about different ETs? What if, say, Titanians want to colonize even colder worlds? Or artilects? Or Venusians? Or cheela? We should search in their typical frequencies too.
Of note on the production of mini black holes … long ago Hawking showed that this may be done in the early universe , very early, it is still an open issue about the existence of these Primordial Black Holes , still a topic of research. Also the artificial production has been investigated for the LHC … see … https://en.wikipedia.org/wiki/Micro_black_hole
A couple of problems about black hole propulsion … how does not manipulate something so massive? It is true the size is roughly that of a nucleus but at 10^9 kg it is had to ‘steer’ around even if it is changed. Another problem is how does one establish a stable configuration ? There are extremes stability problems with holding a small black hole in place with respect to the propulsion reflector.
When speaking of extracting energy from a black hole one might use Superradiance from a small rotating black hole to better effect …..https://en.wikipedia.org/wiki/Superradiance
” In fact, it turns out that if the initial singularity is as small as about 200 kg, and fired into a mass of steel, it will gain mass much faster than it losses it, and eventually grow into a singularity as massive as the steel provided.”
I’d need to see the math on this; A black hole of 200 kg would have a “mouth” comparable in size to an elementary particle, emitting an absolute torrent of radiation. And it’s gravity would be negligible even a millimeter away, so it isn’t like it would crush the surrounding matter to neutronium, the way a larger black hole would.
It seems to me that it would surround itself with a high temperature, low density plasma bubble, and hardly feed itself at all.
You make a good point about the size of the BH, its gravity, and radiation. Even assuming it could be injected into a mass, it is more likely to become a bomb than a furnace.
Although Clarke’s vision of the Sakharov Drive in “Imperial Earth” was likely incorrect as it was not emitting Hawking radiation (The BH mass was about 1000 kg), he was probably more practical in using it to heat hydrogen to create a rocket exhaust. This would be fine if the BH did not emit HR, but since it probably does, his BH drive in the Sirius spaceship is not feasible.
I would have thought that if large scale energy beaming is feasible, then this will be the best way to power fast interplanetary spacecraft using electric engines. If so, Frank Hampson got there first with his “impulse power” for Space Fleet spaceships in his Dan Dare comic in the 1950s.
New ways to mine existing databases: Dr. Zubrin offers very interesting insights. The idea that great civilizations discoverable by amateurs, may be hiding in datasets right under our noses is a prospect too good to pass up. It could even include tickets to Stockholm.
How can this be done as it will evaposate faster than the time to reach the interior of the steel ball?
Given that there are simpler alternatives to powering minisuns and starship engines, this approach begs teh question “why the BH solutions to solve the problems?” Worse, the problems that can be solved are limited to the solutions offered. Slow, massive starships. Space habitats of certain sizes. Technologies tend to expand possibilities. BHs as energy sources seems to limit them, and therefore, IMO, are not generally useful to solve the few problem spaces raised.
But it may not be a singularity but a Planck core or Planck star.
https://futurism.com/what-are-planck-stars-how-do-they-differ-from-black-holes
What Are Planck Stars? How Do They Differ From Black Holes?
Envisioning A Planck Star:
“Of course, if one of these “objects”exist, it would be incomprehensibly small (even compared to an atom), with a diameter of around 10^-10 centimeters. Still yet, it would be around 30 orders of magnitude larger than the Planck length (one is equal to 1.61619926 × 10-35 meters).
As to how a Planck star would look to an observer, and this is the really interesting part, the effects of time dilation would factor in. Time, as it goes, doesn’t run the same for everyone, everywhere. It flows differently from the surface of Earth than in low-Earth orbit… though the effect is negligible. The rate at which time ticks is really thrown for a loop when we venture far beyond the most massive stars and planets, into orbit around intermediate to supermassive black holes—objects so dense and with such powerful pulls, nothing… not even light… can escape.
In fact, before light even enters the event horizon, it begins to feel the drag of time dilation. We can’t be sure—to reiterate, we don’t know what happens inside black holes—but some of the best minds in the world have suggested that time nearly comes to a complete standstill. Yet nothing appears amiss from the outside looking in.
If this is confusing, think back to the water world featured in ‘Interstellar.’ (Spoilers, obviously) Because of its proximity to Gargantua—the black hole/wormhole the crew traveled through—what was an hour to the people on the ground was years, decades even, elsewhere. Because of this, and despite the fact that the first human landed on the planet nearly a decade beforehand, it’s probable that the female astronaut had only been there for a few hours when the second group arrived. Her pulse beacon was still active, yet no new transmissions were seeping out.
Even so, any such Planck star may only live for a short while before the ‘bounce:’ about the “length of time it takes for light to travel across it.” However, to an outsider, it would appear to last for millions, even billions, of years… continuing to exist alongside the black hole itself.”
This has long been an appealing idea, but it does imply that it is possible to convert matter directly into antimatter (or energy). If there are indeed no physics bookkeeping obstacles to doing this using a black hole catalyst, it might also be possible to implement as an atomic-scale total conversion reaction. It is possible that it is much easier to research this technology than to create an artificial black hole.
Still, it can’t hurt to look. By the way: do you think it will ever be possible to identify gravity waves from evaporating black holes of primordial or artificial origin?
Great minds think alike. The Romulans of Star Trek powered their ships with an artificial singularity drive.
https://memory-alpha.fandom.com/wiki/Romulan_technology
The problem with mini black holes is that they don’t hang around very long and they explode when they evaporate according to Hawking. One would still need very high energy conditions to make them and I think they would have to violate some physical laws like the Schwarzschild radius and Chandrasekhar limit. They would have to be gravitation energy concentrations.
Quantum black holes in my opinion can’t really be called black holes. There is no event horizon and they behave more like high energy particles which decay very quickly in a very small fraction of a second. Quantum black holes, Reality Bending Black Holes, Scientific American special edition, 2007. Hawking wrote that mini black holes explode and give off radiation when they evaporate.
I think black holes may have too much energy and gravity to be useful. One would not have to worry about moving it since it would move the spacecraft towards it. If the black hole was outside or in front of the ship, the gravitational energy would be much too high long before the gravity of a black hole was reached. The ship would be torn apart by tidal forces and the pieces would fall into the hole. If the black hole was inside the ship, then the body of the ship would implode along with it’s occupants, propulsion system and energy generating engine in a flash of light and disappear.
Also the idea of designer black holes with the accumulation of matter is science fiction since a 200 kg black hole has to be crushed down beyond it’s Schwarzschild radius in order to have an escape velocity greater than light to make a black hole and needs a very large amount of energy to compress it. One has to get that energy from somewhere since such a black hole does not naturally exit in physical reality in normal energy conditions in space time. One would have to make that energy artificially like gravity waves. How do you do that? If we can, then we can throw out the need of the black hole and the Schwarzschild radius.
Yes, I too like the Star Trek idea of a quantum singularity being in a Romulan war bird, but it is probably unnecessary and science fiction. Positive energy is needed for a warp drive to make negative energy, but do we need make black holes?
Also it is interesting to do a thought experiment to see what happens to a person if they fell onto a neutron stars. They actually would be crushed into atoms or ions and electrons. The magnetic field of a neutron star is 100 million times stronger than Earth’s magnetic field and a magnetar neutron star’s magnetic field is a quadrillion times stronger than Earth’s. The gravitational tidal forces would rip one apart and the magnetic field would tear apart the electric forces in one’s molecules. The surface temperature of a neutron star is 2 million degrees. The molecules would be torn into atoms which have some of their electrons stripped off so they would be ions. Some protons may combine with electrons to make neutrons, but I don’t know for sure if the gravity is strong enough near the surface of the neutron star to do that.
Yet Robert Forward in Dragon’s Egg built up a scenario in which xenobiologic beings – the chela – lived on the surface of a neutron star.
All this sounds interesting, but it has a fundamental problem. As the mass density of a shrinking body increases, the increasing gravitational field causes time delation. So, relativistically, the complete formation of a black hole cannot be observed as it will take infinite time for an outside observer. So, while the gravitational effect from outside will be as that of a black hole, an event horizon will never be formed. And it is exactly the event horizon that is needed for Hawking’s radiation.
Hi Paul & Dr Z
Fascinating revisit of Crane & Westmoreland’s ideas. A reference that is indispensable, and 40 years old, when talking Black Hole Starships is Robert Freitas’ “Xenology” (1979), specifically this section: 17.3.5 Total Conversion Drives
A couple of small quibbles. Clarke’s “Asymptotic Drive” used the accretion energy of the black hole – some 6.4 watts/kg – which has an efficiency of over ~5% converting mass to energy, with an exhaust velocity of 0.33 c.
Sheffield’s ‘kernels’ stored rotational energy and were effectively big batteries. Ok for interplanetary flight. When going interstellar McAndrews, Sheffield’s slightly Scottish protagonist, used Zero Point energy to power his “Balanced Drive” starships.
A final thought: With so many interstellar planets for every star – Louis Strigari’s estimate was about ~100,000 – the available real estate for illumining with mini-Black Holes is phenomenal. However, I don’t think Hawking radiation is sustainable in the long term. Force feeding a sub-proton scale event horizon is a non-trivial task and I’d be interested in how Dr Z hopes to do so at 1 kg/s.
regards,
Adam
“The ideal thrust T of a rocket with jet power P and exhaust velocity v is given by:
T = 2P/v (2)
So with T = 13,700 TW and v=c = 3e8 m/s, the thrust would be 8.6e7 N. ”
in saying that T = 13,700 TW didn’t you mean to say that P = 13,700 TW ??
It’s actually a pulsar that has a 100 million times strong magnetic field than the Earth. Pulsar’s eventually loose angular momentum and the spinning becomes much slower but one would still be squashed to atoms if a human tried to land on one. I can’t imagine any kind of life that could survive the high surface temperature, electromagnetic field and gravity on the surface of a neutron star.
But Robert Forward could.
https://en.wikipedia.org/wiki/Dragon%27s_Egg
So did Stephen Baxter – Flux.
The nonlinear optimisation of the flight profile for a multi-BH craft based on Crane & Westmoreland’s “Hawking Rocket” concept produces spectacular results. It does however require the ability to create or corral BHs of carefully chosen sizes before beginning the journey. No in-flight mass-feeding assumptions need be made to produce unsurpassed subluminal performance. The trick is to assemble the correct collection of masses such that one may jettison a BH which is about to expire just before the next-smallest BH begins to produce prodigious thrust. A mini-BH at end of life is not something you want to be around, since its power output will destroy any nearby artificial structure with ease.
Dr. Zubrin, your ideas are fascinating to say the least. Orbital ASP’s as power sources is an awesome potential way to warm otherwise uninhabitable planets. If we ever discover a sunlike but small body orbiting a planet we have a possible explanation already lined up!
My favorite part of your article was this paragraph though:
“One of the great mysteries of science is why the laws of the universe are so friendly to life. Indeed, it can be readily shown that if any one of most of the twenty or so apparently arbitrary fundamental constants of nature differed from their actual value by even a small amount, life would be impossible [9]. Some have attempted to answer this conundrum by claiming that there is nothing to be explained because there are an infinite number of universes; we just happen to live in the odd one where life is possible. This multiverse theory answer is absurd, as it could just as well be used to avoid explaining anything. For example take the questions, why did the Titanic sink/it snow heavily last winter/the sun rise this morning/the moon form/the chicken cross the road? These can all also be answered by saying “no reason, it other universes they didn’t.” The Anthropic Principle reply, to the effect of “clearly they had to, or you wouldn’t be asking the question” is equally useless.”
Great logic doctor. The unprovable, untestable infinite universes concept as an answer to the fine tuning “problem” is absurd, as you succinctly say. Fine tuning isn’t a problem, it is evidence demanding a more reasonable answer.
These objects should be very bright in the Infrared to Microwave bands. The nearby M Dwarfs would be easily visible to our eyes if they extended into the infrared frequencies. One of the interesting points of images supposed alien beings is the large black eyes, which makes sense if they came from planets orbiting M dwarfs or ASP’s. The longer infrared to microwave frequencies requiring a larger lens!
There is a trouble with shells around smaller mass microBHs, because photons with more than 100 MeV of energy will photodisintegrate nuclei, and the shell will degrade quite quickly. Maybe there is a way to use larger singularities which emit gamma rays below photodissociation threshold. Something like a “planetary” system of singularities, with large one in the center, several smaller “planets” in orbits around them, and several “moons” around each planet that are primary energy sources. Or, maybe, even a spherical cluster of 10^5…10^7 singularities with mean inter-BH distance calculated so that GW decay is small.
But the problem of creating micro BHs dwarfs all that.
First, converging gamma ray lasers would not produce black hole with energy density more than photon-photon pair production limit, because vacuum becomes opaque when it is reached. For GRB photon energies it’s in the order of 1e27 J/m^3 [https://www.slac.stanford.edu/cgi-wrap/getdoc/slac-wp-020-ch05-Sari.pdf]. To create even a BH the mass of the Moon, 1e51 J/m^3 energy density is needed, and even if we’ve found a way to focus the needed energy into needed space, converging gamma rays would rip the hell out of vacuum and scatter off that long before reaching critical density. And the minimum mass of BH that could be formed this way is in fact much bigger than stellar class limit (in the IMBH range)
Second, it seems that colliding relativistically accelerated projectiles
is very unlikely to produce BHs smaller than the transverse dimensions of projectiles. And when calculated, it turns out not much easier than kugelblitz approach. For nucleus-sized BHs and projectiles the needed energy is many orders of magnitude higher than Planck energy per quark. The projectiles accelerated to the energy of Oh-My-God Particle per nuclon (1e33 J/m^3 if made from densest metals) need to have much more than one solar mass equivalent of kinetic energy to create BH with head-on collision for spherical shapes. And long threads with length orders of magnitude bigger than width, make only a minor difference. If a civilization can accelerate ten-kilometer-long spears of osmium to OMG-particle speeds, and collide them head-on, why it needs an energy source for terraforming? And the terraforming itself? It’s Kardashev III+ class endeavour both in terms of needed power and space.
And to make a 3 solar mass black hole, one only needs to find two neutron stars and steer them into each other.
The difficulty gap between creating 3 solar mass black hole and 0.3-solar-mass one while not violating some deepest laws of nature is such that the gap between inventing bicycle and creating antimatter-powered O’Neill cylinder capable of travelling to M87 (while preserving biosphere inside) is nothing compared to that…
@Paul Leyland You are right about the magnetic field and electric forces. The electrons ejected from the surface of a pulsar are from the magnetic field which is very strong. The electric force is stronger than the gravitational force in normal conditions, but not inside the center of the neutron star. The Pauli exclusion principle between the protons and electrons is overcome by the gravity which compresses the electrons and protons into neutrons where electric forces between the atoms have been overcome.
Hi Paul
The artificial Black Hole Sun concept is inspiring TBH. Especially if they’re thawing out the thousands of interstellar planets out there. Interstellar travel will have a whole new meaning and destinations merely fractions of a light-year away. A Type II Civilization could create an Empire of NuStars with worlds in the thousands. Further afield, a vast system of planets and their NuStars could be orbited around a Super-Massive Black Hole on a vast scale. Billions of worlds could be within the reach of interplanetary vehicles.
The premise of using black holes for lighting or ambient energy collection surprises me. Isn’t it simpler to send a comparably sized megastructure into close orbit around a nearby star to generate many collimated beams for lighting, spaceship propulsion, and simple industries? (That and the occasional interstellar laser war) It seems like overkill to make a black hole that can evaporate in a few years in a world-shattering explosion, if you don’t intend to use it for comparably ambitious purposes.
If our universe is an artificial black hole built in this way, perhaps the singularity’s buildup period is what caused the inflation.
ISTM that major questions re: ASP are whether/how BH can be:
1) Created
2) Fed
(There have been disputes here in both of these.)
Can these questions be answered theoretically or will it require experimentation?
Thank You,
Keith Halperin
This is interesting:
http://www.spacedaily.com/reports/A_new_paradigm_of_black_hole_physics_leads_to_a_new_quantum_999.html