Can we tap ionized particles in the interstellar medium as a way of exchanging momentum for propulsion? It’s a concept with a lot of pluses if it can be made to work, chief among them the fact that such a device would be propellantless. Looking at the topic today is Drew Brisbin, a postdoctoral researcher in astronomy who received his PhD from Cornell University in 2014. Dr. Brisbin has since gone on to work towards better understanding his field of specialization: the study of galaxy evolution in the early universe. He currently works at Universidad Diego Portales, in Santiago Chile, where he collaborates closely with other researchers using some of the most sensitive telescopes in the world, located in the mountainous Chilean desert. In addition to his formal work and outdoors-oriented hobbies, he also enjoys dreaming about the future of humanity. One particular dream recently seemed to warrant some further investigation, leading him to the ideas he explains today.
By Drew Brisbin
Foreword

This article represents a distillation of a work published in April 2019 in the Journal of the British Interplanetary Society (reference [0]). Some technical details have been omitted for brevity, but interested readers are encouraged to read the original publication which is freely available at https://arxiv.org/abs/1808.02019. Additional commentary has been included to address what the author sees as a critical flaw in Dr. Robert Zubrin’s “Dipole Drive” concept.
Abstract
In particular light of the recent public excitement and ensuing disappointment regarding the exotic “EM drive” it is worthwhile to point out that space travel without on-board propellant is eminently possible based on well established physical principles. Here a new mode of transport is proposed which relies on electric-field moderated momentum exchange with the ionized particles in the interstellar medium. The application of this mechanism faces significant challenges requiring industrial-scale exploitation of space but the technological roadblocks are different than those presented by light sails or particle beam powered craft. This mode of space travel is well suited to energy efficient travel at velocities below about five percent the speed of light (0.05 x c) and compares exceptionally well to light sails on an energy expenditure basis. It therefore represents an extremely attractive mode of transport for slow (of order multi-century long) voyages carrying massive payloads to nearby stellar neighbors. This will be a useful niche for missions that would otherwise be too energy intensive to carry out, including initial forays into nearby stellar systems with observatory probes, or long term transport of bulk materials as a precursor mission to set up colony infrastructure.
Introduction
The tyranny of the rocket equation has long been recognized as an impediment to becoming a truly spacefaring species. Due to the exorbitant reaction mass required for traditional rockets in interstellar travel, there has been considerable attention to methods of space travel that circumvent the rocket equation. Laser-driven light sails are a prominent and long-standing idea (see for example [1] and references therein). While light sails are well established and also the engines of the widely publicized Breakthrough Starshot program [2] and Project Dragonfly [3], their thrust is fundamentally limited to 6.67 N/GW. For comparison, the Three Gorges Dam, the largest capacity power plant currently in operation, has a capacity of about 22.5 GW. If this power was transmitted with perfect efficiency to a light sail it would provide thrust equivalent to the force required to lift a 15 kg mass on Earth. Scaling light sails up to larger-than-gram-scale spacecraft therefore necessarily depends on humanity’s ability to harness incredible power. Furthermore, since light is only able to push, it is very difficult for light sail spacecraft to slow down at their destination, limiting missions to fly-bys unless complicated reflecting infrastructure can be sent ahead of the craft. Alternatively, direct sunlight could be used as a source of photon pressure. Unfortunately, the material properties suggested to be necessary for a practical interstellar solar sail require materials with extremely low areal densities with σ≲10-3 g/m2 [4]. Current state-of-the-art reflective films developed for light sails reach areal densities of order 10 g/m2, or four orders of magnitude too dense even without including any support structure or payload, so it is uncertain when if ever suitable materials will be developed for an interstellar solar sail [5].
Another idea using external reaction mass is the particle-beam powered spacecraft. This hinges on a sail formed by an extended electric or magnetic field which is able to deflect a remotely-beamed stream of charged particles. Since charged particles carry much more momentum per unit energy than photons this could have much lower power requirements than light sails. This concept has its origins in the Magsail, a large loop of current carrying wire which deflects passing charged particles in the interstellar medium (ISM), eliciting a drag force which could be used as a brake to slow spacecraft down to rest with respect to the ISM after a high speed journey [6]. To provide acceleration, one could simply supplant the ISM with a beamed source of high velocity charged particles [7]. Providing a long distance beam of charged particles is, however, quite difficult because of beam divergence due to particle thermal motion, interaction with interplanetary or interstellar magnetic fields, and electrostatic beam expansion in the case of non-neutral particle beams. Andrews (2003) suggests that it would be necessary to construct a highway of beam generators at least every AU or so along the route on which the craft accelerates [8]. The related concept of the electric sail instead uses an electric field generated by a positively charged grid of wires or wire spokes extending from a central hub to push against the outward streaming solar wind [9]. This concept has the near term potential to allow travel within our own stellar neighborhood with very low energy costs. The electric sail, like the Magsail however, ultimately relies on a drag force, decelerating the spacecraft to rest with respect to the surrounding medium (the outward moving solar wind in this case). It is therefore unable to accelerate beyond the heliosphere, nor can it accelerate directly inwards towards the sun while in the heliosphere.
It would be possible to overcome these obstacles by actively pushing against the charged particles of the ISM, rather than passively coming to rest with respect to the medium. These spacecraft with interstellar medium momentum exchange reactions (SWIMMERs) can accelerate with respect to the ISM, are significantly more energy efficient than light sails, would be able to decelerate at their destination, do not require pre-established infrastructure along the route and are based on elementary physical principles. Recently Dr. Robert Zubrin discussed his independent work on a “dipole drive” concept which is similar to the SWIMMER concept described here [10,11]. Although the two ideas are related and even share a similar geometry, they were arrived at independently. Furthermore the dipole drive as described, suffers from a flaw which prevents its successful acceleration in the stationary ISM. The work presented here concerns the conceptual mechanism which allows SWIMMERs to accelerate through a stationary ISM.
Both the Magsail and electric sail concepts rely on the fact that there is significant mass in the ISM (or the heliosphere) which can interact with relatively low mass structures consisting of charged or current carrying wires. How, then, could a spacecraft interact to accelerate rather than decelerate with respect to the surrounding medium?
The need for a time varying electrical voltage
Quite generally this will require a time varying electric field which can do work on the surrounding particles of the ISM. As a thought experiment, imagine a spacecraft consisting of a pair of conducting plates arranged in a parallel-plate capacitor style configuration with a switchable power source connecting them and able to charge and discharge them at will. The conducting plates, rather than being solid, are composed of a wire mesh with the vast majority of the area taken up by open space rather than metal, such that particles are easily able to pass through the plate mesh without collision. The spacecraft is moving face on through a stationary medium of charged particles (like the interstellar medium), as shown schematically in Fig. 1. For the moment take the charged particles to be macroscopic and extremely dispersed so we can easily see individual particles and identify when they are in the vicinity of the spacecraft — charged pebbles rather than atoms or elementary particles. As the spacecraft moves through the field of charged particles we can strategically switch the power source on and off to create an electric field and push on charged particles as they pass between the conducting plates, accelerating the particles backward and creating thrust to push the spacecraft forward (Fig. 1). This scenario is perfectly in line with conservation laws. momentum is conserved since the particle gains momentum in the backward direction and the spacecraft gains momentum in the forward direction. Energy is conserved as the increase in kinetic energy (of the particle and the spacecraft) is drawn directly from the power source depleting whatever energy source is being used (depleting a battery’s chemical energy, or converting beamed laser light for instance).
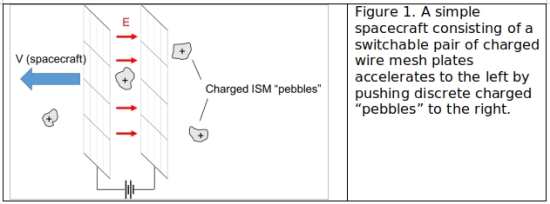
In practice of course, the ISM is not made of macroscopic, easily separable pebbles, but microscopic ions and electrons with tens of thousands per cubic meter or more, so we cannot consider manually switching the charged plates based on the positions of individual particles. The possibility of simply leaving the plates continuously charged, front facing plate positive, back plate negative, may initially seem workable, and this appears to be the scenario imagined in the “Dipole Drive” [10]. Introductory electricity courses train us to think about parallel plate capacitors as having a strong field in one direction between a pair of charged plates, and no field outside the plates, so it is easy to initially imagine that a positively charged ion would approach the front plate while feeling absolutely no force, feel a strong force backwards while between the plates, and then feel absolutely no force again as it recedes beyond the back plate. In fact, however, a set of finite parallel plates will indeed have electric fields outside of their gap which directly oppose the electric field inside the gap, and would perfectly negate the thrust generated by particles transitioning the gap.
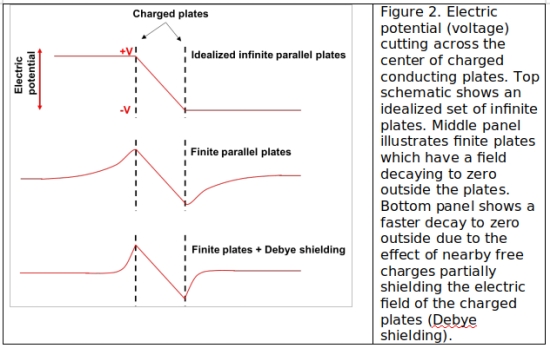
This is made more clear by considering the electrical voltage rather than electric fields. Fig. 2 (top) shows schematically the voltage through the center of an idealized infinite parallel plate capacitor charged to a potential difference of 2V. Positive charges will want to “slide down” the potential ramp located between the plates, accelerating rightward. For a finite sized set of parallel plates the voltage extends a bit to the left and right of the gap, continuously decaying from the voltage at the plates to a voltage of zero at great distances as shown in Fig. 2 (middle). Note that these voltage ramps tilt in the other way than the region between the plates and will tend to accelerate positive charges in the opposite direction. For a particle entering in from the left and making it all the way through to exit out the right side, would it end up with more or less rightward velocity? Remember that voltage (often referred to as electric potential) is simply potential energy divided by charge (in SI units 1 volt = 1 joule/coulomb). Starting out very far on the left in Fig. 2, the rightward traveling particle with charge q will have some kinetic energy, KE, and zero potential energy.
As it approaches the front plate, it will begin slowing down as it rises up the potential ramp and converting kinetic energy to potential energy, eventually reaching a peak potential energy of +qV (with a kinetic energy of KE-qV). As it traverses the gap it is accelerated rightward as it slides down the potential, eventually reaching a potential energy of -qV and a kinetic energy of KE+qV. It then exits the parallel plate gap and is again forced up a potential ramp, converting kinetic energy back into potential energy, until it finally reaches distances far away from the plates where the voltage is 0 at which point it has potential energy 0 and kinetic energy KE — exactly the same as it started.
This is not a minor fluke of this particular geometry either. Any arrangement of charged plates – so long as the voltage is finite and the plate volume is finite – will leave the potential 0 at infinity. In [11] Zubrin has suggested that Debye shielding (the phenomenon of oppositely charged free particles in a plasma tending to cluster around charged objects and screen out the electric field) would somehow ameliorate this issue, but that is not the case. The effect of Debye shielding will be for the front facing positive plate to accumulate a cloud of electrons and the back plate to accumulate a cloud of positive ions, making the voltage ramps just outside the plate pair more steeply return to zero, as shown in Fig. 2 (bottom). Nonetheless, the potential remains 0 at large distances and in the end passing particles enter and leave the system with the exact same kinetic energy. This does not preclude the particles from changing direction, either being reflected back in the direction they came, or deflected to the side if they interact with the parallel plates at an angle, so such a configuration could certainly be used to either steer or decelerate with respect to the charged particle medium, but such a system with constant voltages cannot do work on charged particles which begin and end far away, and cannot accelerate with respect to them (it could still be useful to accelerate up to the velocity of the solar wind inside our heliosphere, much like the electric sail).
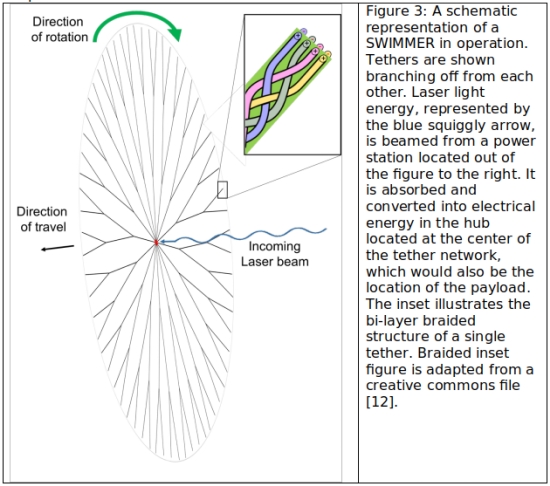
If the goal is to accelerate in the dead of the ISM, it is essential that a time-varying electrical potential be used to do work on the passing particles. There are multiple ways to do this, but one simple implementation, illustrated in Fig. 3, could feature a pusher plate made of a large grid of wires moving face-on through the ISM (much like the proposed geometry of a standard electric sail). Unlike a standard electric sail, however, the grid of wires would actually be two identical layers of wire sandwiching a strong insulator between them to keep the two layers physically apart and electrically isolated. These wire grids or tethers could be made from very fine superconducting wire and the entire ensemble could be spun to create tension and keep the wire grids extended without heavy support structure. The two faces of the pusher plate would be charged and discharged cyclically. In the “primer” portion of the operation cycle, the front layer in the pusher plate is raised to a positive potential and the back layer to an equal negative potential. Due to edge effects of the finite plates and the self-shielding behavior of plasmas, this results in a decaying electric potential of opposite sign on either side of the plates. Ions streaming towards the front positively charged layer slow down, building up an overdense clump in front of the pusher plate while an underdensity forms at the immediate location of the pusher plate. Then in the “pull” stage of the cycle the potential difference across the layers is reversed and significantly increased. The ion clump that was formed in front of the plate will be attracted to the negative front layer, pulling the spacecraft forward. As the clump approaches the pusher plate, the potential difference is turned off and the clump is allowed to coast through the plate to the other side. In the final “push” stage the same potential difference is applied and the clump is further pushed backwards by the positive back layer of the pusher plate. The clump drifts away beyond the influence of the pusher plate and the cycle repeats. Fig. 4 shows the electric potential and ion density at various cycle stages for a simple model.
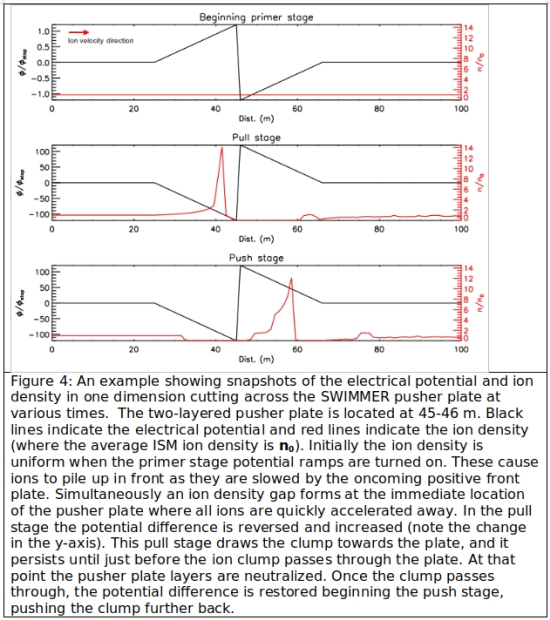
By intentionally setting up clumps in the oncoming ISM we can interact with it much more like in our initial thought experiment with charged pebbles. The spacecraft gains momentum by giving backward momentum to the ISM (pushing ion clumps to the right in Fig. 4). The source of the potential difference does work in the primer stage when it sets up the positive potential, raising the electrical potential energy of the ions in front and again in the push stage when it raises the ion clump to a higher potential. Electrons encountering the potential ramps will largely be reflected but this causes only a negligible momentum drag since they are far less massive than the protons and other positively charged ions. In a real three dimensional case, there will also be loss of efficiency due to particles which do not interact perfectly in one dimension, but instead are pushed off to the side as they pass by the charged wires. Furthermore, this qualitative conceptual analysis does not account for the self influencing behavior of plasmas. This will undoubtedly strongly affect the ion (and electron) distributions and the extended electric potential. Detailed particle-in-cell simulations will be necessary to investigate the optimal tuning of cycle timings, electrical potentials, and even geometry of the charged plates as it may be advantageous in some cases to accelerate ion clumps across a series of potential differences to gain more thrust per ion, at the expense of a more complex and massive pusher plate. These simulations are beyond the scope of this work but will be a critical step in transitioning the concept from a thought experiment to a practical real world device.
Mathematical expression of an idealized case
While the effectiveness and geometry of a SWIMMER will ultimately need to be tested thoroughly by simulation, it is straightforward to represent the force on an idealized system which is able to efficiently convert electrical power, P, into backwards acceleration of nearby particles. The resulting force, FSWIMMER, is
![]()
where mp is the particle mass (of order the proton mass for the ISM), n is the density of particles, v is the velocity of the spacecraft (with respect to the stationary-particle frame), and A is the cross sectional area over which the system can interact with particles (or equivalently v x A is the volume rate of particles swept out by the spacecraft through time). The positive sign is used when accelerating with respect to the the stationary-particle frame, and the negative sign is used when decelerating. The derivation of this relationship is shown in [0].
The power referred to throughout this work is the delivered electrical power. Thus far the source of power for a SWIMMER has been ignored. There is no reason a SWIMMER could not use an onboard power source, making it totally independent of external infrastructure. This, of course, would require an exceptionally energy dense fuel source as well as a very efficient generator to achieve useful velocities for interstellar travel. Beaming power remotely to the SWIMMER is possibly a more viable strategy for interstellar travel, which invites a direct comparison to light sails. In this case an additional P/c term is included in eq. 2, corresponding to the photon pressure of the beamed energy being absorbed by the spacecraft. The total force is then:
![]()
Where P/c is either added or subtracted depending on if the beamed energy source is coming from the origin or the destination respectively. It will also be useful to consider the ratio, R, of the force on a SWIMMER to the force on an ideal light sail with equal delivered power (F=2 P/c). This ratio can be written as:
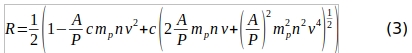
where we have used the the positive signs in the SWIMMER and photon forces indicating the spacecraft is accelerating and beamed energy is coming from the origin (as would be the case for an initial out-bound journey to another star system). In Fig. 5 R is shown as a function of velocity for a few values of A/P. There is some uncertainty surrounding the structure and properties of the local ISM, but there is general consensus that a journey to Cen A will involve passage through some combination of the Local Interstellar Cloud, the Circum-Heliospheric Interstellar Medium and the G Cloud. Therefore, a conservatively low ion density of n=0.07 cm-3, consistent with the estimated densities in these clouds, (see for example [13]) is used in Fig. 5. Fig. 5 shows the force initially rising with velocity due to the fact that at higher velocities the SWIMMER plates are sweeping out larger volumes of the ISM faster and able to interact with more particles per second. The force peaks at some velocity, and then decreases since it takes more and more energy to accelerate the passing ions to yet higher velocities to get the same momentum change. Due to this initial rise in force with velocity, it may be useful to give SWIMMERs an initial velocity boost through other means (such as conventional rockets, gravitational assists, or particle beam assists) to take advantage of the forces at higher velocities.
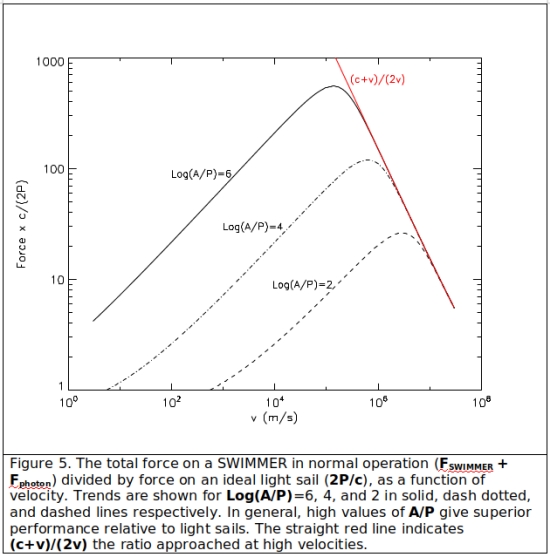
Larger A/P values give significantly better performance at lower velocities, but trend together as velocity increases, with the force approaching (P/v) x (c+v)/c (the ratio R approaches (c+v)/(2v), shown by the red line in Fig. 5). This high velocity limit implies an order of magnitude larger force for SWIMMERs relative to light sails up to v=c/19 or about 5% the speed of light.
Example mission
To illustrate the potential of SWIMMERs for interstellar travel, it is helpful to consider a possible future mission. Further details and technical considerations are available in the published manuscript, but here we simply assume the the engineering difficulties of beaming power to interstellar distances is solved, and the onboard energy converter has a specific power capacity of 4 kW/kg (every 4 kW of delivered power requires an increase of 1 kg in the mass of the power converter equipment). The ISM is assumed to be uniform with a density of 0.07 cm-3, a temperature of 7000 K and therefore an electron Debye length, λD=21.8 m.
A relatively lower mass SWIMMER mission might have the goal of transporting a modest space probe, mpay=1000 kg to α Cen A. Accelerating within our heliosphere and decelerating at the destination are possible, and in fact relatively energy efficient but discussion of these will be left for the main publication, [0], for brevity. A modest electrical power delivered to the SWIMMER of 10 MW is assumed. The pusher plate will be made up of several long tethers. In practice these tethers will consist of very fine braided filaments to prevent failure due to micrometeoroid and interstellar dust collision, as described for the electric sail [9]. From a material mass standpoint these are considered to be single wires with an effective diameter of 30 μm. This is equivalent in material to eight filaments with diameters of about 10 μm. Given the pulsed nature of the SWIMMER electric field, the wire tethers should be made out of superconducting materials. A single charged wire will interact with charged particles passing within about λD on either side of it. The total cross sectional interaction area is given by
![]()
where L is the summed length of all the tethers. This cross sectional interaction area is somewhat of an idealization as the Debye length does not represent a hard cut off where particles suddenly cease to be effected by an electric field, and in regions where tethers intersect, part of their cross sectional areas will overlap. Nonetheless it is a sufficient estimate for our rough calculations. The mass devoted to this pusher plate will be mpusher= ρ x L x π rwire2. Where rwire represents the effective radius of the wire tether (15 μm in our case), and ρ represents the density of the tether material, which we will take to be 2570 kg/m3, the density of the popular superconducting material, magnesium diboride.
The total mass of the SWIMMER ship is comprised of mpay=1000 kg, mpower=2500 kg (given by the 10 MW supplied electric power and a 4 kW/kg specific power), and mpusher. We will take 7400 kg as the mass of the pusher plate which provides for a total summed tether length of 4.1 x 109 m. While this is seemingly a very long tether, it does not in any way represent the spatial scale of the SWIMMER, as the pusher plate will be made up of several thousand tethers, possibly splitting off from each other at greater radial distances. The summed length is merely a useful value for determining the total cross sectional area in plasmas of different temperatures and densities. In this case, from eq. 4 our SWIMMER tether length corresponds to a cross sectional interaction area of 180,000 km2 (about the size of Uruguay or the state of Washington).
We will begin our voyage as the SWIMMER enters the ISM at 100 AU with a velocity of 4.0 x 105 m/s (0.133% the speed of light and consistent with typical velocities of the solar wind). Iteratively integrating using eq. 3, we find that after just less than 300 years the spacecraft will be on the doorstep of Alpha Centauri after having travelled one parsec and achieving a final velocity of 1.66% the speed of light. Including time to initially accelerate from rest within the heliosphere and decelerate at the destination marginally increases the trip time, but we could also shorten the trip slightly by systematically shedding mass and reducing the size of the pusher plate enroute. As Fig. 5 shows, at higher velocities larger plate areas provide diminishing returns, so as the spacecraft reaches higher velocities the larger area of the pusher plate becomes dead weight. A total journey of about 300 years starting from rest in the solar system to being gravitationally captured by Cen A is reasonable for the overall journey [0].
While 300 years is a significant amount of time for a scientific endeavor, there is good precedent for multi-century science projects for worthwhile investigations (c.f. [14-16]). Furthermore, the energy expense is a pittance compared to an equivalent mission using laser-pushed light sails. An equivalent, 7400 kg probe pushed by 10 MW of laser light incident on ideal light sails (and starting with a velocity 4 x 105 m/s) would take about 1600 years to travel 1 parsec and reach a final velocity of 0.28% the speed of light. To reduce the light sail travel time to 300 years would require an average power consumption of nearly 700 MW (70x higher).
Conclusion
SWIMMERs represent a new mode of interstellar transport. By disposing of onboard reaction mass they circumvent the rocket equation, and by exchanging momentum with ions in the ISM they improve by orders of magnitude over the energy efficiency of traditional light sails at relatively low velocities. The key to this momentum exchange is the time varying electric field which allows SWIMMERs to create inhomogeneities in the surrounding plasma and then push on these inhomogeneities to create thrust.
SWIMMERS perform exceptionally well at lower velocities, with their advantage over light sails diminishing quickly at v > 0.05 c. Furthermore, by relying on the ambient ISM as a momentum exchange medium, they are quite versatile, able to accelerate either away or towards a beamed energy source, opening up myriad opportunities to serve as one-way transport, roundtrips or even statites remaining in stationary positions with respect to the Sun and serving as useful waypoints with infrastructure for other potential space transportation networks.
The example discussed here only scratches the surface of the possible roles for SWIMMERs in our spacefaring future. Their characteristics make them ideal for any mission with large masses in which relatively low velocities are acceptable. They are unlikely to be the sole mode of space transport due to their diminishing advantages at high velocities and their structural complexity which requires onboard power conversion systems with significant mass. They can play the role of the proverbial Mack trucks of space, transporting goods slowly and reliably at a low energy cost, while more time sensitive cargo can make use of fast yet inefficient light sails – the Ferraris of space. SWIMMERs might, for instance, be well suited to aiding the construction of a fast interstellar highway by transporting massive particle beam stations along with their fuel supply out to stationary positions between us and our target destinations. These particle beam stations could be used to swiftly carry low mass Magsails along the path or augment the power of future SWIMMERs by replacing the stationary ISM with a corridor of fast moving beamed particles.
The mission analyzed here regards a one-way interstellar trip. While it does push the limits of current technology by assuming relatively high specific power electrical systems, very thin mass-produced super conducting wire, and low mass electrical insulators which can resist large potential differences (as well as very large laser array optics which are addressed in other works regarding light sails) there is no obvious material or theoretical limits which would prevent such missions from realization. Future work in this vein will need to examine several issues ignored here. Areas of further investigation, include the efficiency of the SWIMMER drive in three dimensions; the electrical potential and cycle timings during the pulsed SWIMMER operation and how they effect the required current density of the tethers; the expected impact of interstellar dust collisions and redundant tether configurations to avoid catastrophic damage from tether breakage; and realistic limits on power conversion system capabilities.
As our understanding of interstellar travel develops, we must face the realization that, not only is it difficult, but there is no one-size-fits-all solution. Where SWIMMERs excel in one metric, other methods may excel in another. Ultimately our best strategy is to develop all possible methods in the hope that their synergy will provide a means to accomplish our goals.
References
0. D. Brisbin, “Spacecraft with interstellar medium momentum exchange reactions: the potential and limitations of propellantless interstellar travel”, JBIS, 72, pp.116-124, 2019.
1. R.L. Forward, “Roundtrip Interstellar Travel Using Laser-Pushed Lightsails”, J. Spacecraft and Rockets, 21, pp.187-195, 1984.
2. P. Lubin, “A Roadmap to Interstellar Flight”, JBIS, 69, pp.40-72, 2016.
3. N. Perakis, L.E. Schrenk, J. Gutsmiedl, A. Kroop, M.J. Losekamm, “Project Dragonfly: A feasibility study of interstellar travel using laser-powered light sail propulsion”, Acta Astronautica, 129, pp.316-324, 2016.
4. R. Heller, and M. Hippke, “Deceleration of High-velocity Interstellar Photon Sails into Bound Orbits at Centauri”, Astrophysical Journal Letters, 835, pp.L32, 2017.
5. D. Spieth, and R.M. Zubrin, “Ultra-Thin Solar Sails for Interstellar Travel–Phase I Final Report”, NASA Institute for Advanced Concepts, Pioneer Astronautics Inc, 1999.
6. D.G. Andrews, and R.M. Zubrin, “Magnetic sails and interstellar travel”, JBIS, 43, pp.265-272, 1990.
7. G.A. Landis, “Interstellar flight by particle beam”, in AIP Conference Proceedings, vol. 552, pp.393-396, 2001.
8. D.G. Andrews, “Interstellar Transportation using Today’s Physics”, Conference proceedings, American Institute of Aeronautics and Astronautics, 4691, 2003.
9. P. Janhunen, “Electric sail for spacecraft propulsion”, J. of Propulsion and Power, 20, pp.763-764, 2004.
10. R. Zubrin, “Dipole Drive for Space Propulsion”, JBIS, 70, pp.442-448, 2019.
11 R. Zubrin, “The Dipole Drive: A New Concept in Space Propulsion”, 70th International Astronautical Congress (IAC), Washington DC, October 2019.
12. Stilfehler, “technique of 4 strand braiding”, Wikimedia Commons file (licensed for sharing and adaptation), https://commons.wikimedia.org/wiki/File:4_Strand_Braiding.png, last accessed on 18 March 2019. Cropped and edited for 3-d effect.
13. I.A. Crawford, “Project Icarus: A review of local interstellar medium properties of relevance for space missions to the nearest stars”, Acta Astronautica, 68, pp.691-699, 2011.
14. A. Kivilaan, and R.S. Bandurski, “The one hundred-year period for Dr. Beal’s seed viability experiment”, American Journal of Botany, 68, pp.1290-1292, 1981.
15. R. Johnston, “World’s slowest-moving drop caught on camera at last”, Nature News, 18, 2013.
16. C. Cockell, “The 500-year microbiology experiment”, Microbiology Today, 95, pp.95-96, May 2014.



This is a fascinating idea for a star drive, but it would benefit us to bring it down to Earth. Can you make a device with brushes to inject small amounts of alternately positive and negative ions into moving air, when then pushes on them with waves of alternating positive and negative voltage? A smarter ionolifter, in other words. I have daydreamed of it as a means of aircraft propulsion, but more importantly, for replacing the appalling drone of the air blowers that appropriate the top floor-and-a-half of modern buildings, and the ears of all their neighbors, beyond all sense or proportion.
The craft as envisaged here wouldn’t be good for that — too big and fragile I suspect. But that is indeed an exciting area of research! You’re probably already familiar with it, but in case not, an MIT group has been making interesting steps towards a no-moving parts ion propulsion system that works in our atmosphere: https://www.nature.com/articles/s41586-018-0707-9.
This isn’t my field, so no, I was not – very impressive!
There is another technology that we have had that will get us to that 1 to 5%of the speed of light. Project Orion .I was going through some old company documents about a dispute over depletion rates of mineral with the IRS . That was big in the fifties so was an idea by the Pentagon called Project Orion. In these documents is a Wall Street journal because of a front page tax article.But on Page 2 is
Pentagon to review proposal to Develop Rocket propelled by small atomic blasts.
It was to cost billions then and be used to lift massive objects into orbit.
There has been a readability study by General Dynamics funded by ARPA
They were going to do a follow-up because there were some issues.Those issues were the fall of from Earth launches. GD came up with a rough design Of course now if used for interstellar we could launch it from day the moon and avoid the main issue.
There was also a Project Pluto which was to design a nuclear powered craft.
The name of this Project was Orion of course. Other details were classified . The date was Wednesday July 1 1959.
You got that right:
https://centauri-dreams.org/2016/09/16/project-orion-a-nuclear-bomb-and-rocket-all-in-one/
As I said in my essay above and will keep repeating, if we do not develop Orion I can think of one other nation that is quite capable and willing to do so.
Project Orion is pretty well known and there are some good Youtube documentaries about it (actually, Youtube uploads of TV documentaries).
One of them has lots of original footage as well as interviews with Dyson’s son.
Also widely discussed here on Centauri Dreams. A search in the archives will pull up a good many articles.
A few obvious issues that I see with the idea:
1. The ISM has a distribution of particle sizes and charges. Just like the use of a mass spectrometer to separate charged molecular fragments by time of flight, the electric fields of this device will pull and push the particles it interacts with a possibly too wide dispersion in space to allow this “pulse engine” approach to work. IOW, rather than getting a reasonably tight distribution of charged particles as envisaged, teh distribution will be far wider. At the very least, this would reduce the thrust/power of the propuslion system.
2. The beamed power from the laser will still be subject to dispersion over interstellar distances, being particular critical when power is needed to decelerate the craft. This means that the laser power will need to be increased to compensate, perhaps completely negating any thrust/power advantage over photon sails that will get most of their beamed energy closer to the home system and coast much of the way to the target star system.
3. A minor point. The reference design of 180,000 km^2 means a radius of 240 km. Is the design deployable as a spinning device? Will any uneveness in the mass and distribution of the accelerated ions across the surface cause problems for the stability of the design?
What I would like to see with this idea, as well as other theoretical ideas propped up by idealized equations, is some experiments with small test devices. A small mesh in a vacuum tube with charged ions being fired at the mesh should be able to demonstrate several features of the theoretical model. Do the ions bunch up in the priming phase? Do the ions leave the device with a higher net velocity than they started with when emitted? It is the sort of experiment that an engineering or physics lab could set up and be run by students who have the time to test the effects of adjusting the electric field cycle rate vs the incoming ion stream velocity distribution. Once the theory is confirmed, only then should effort be made to create a small test device and test it in space, e.g. facing the incoming solar wind.
All valid points. To reply to point 1, the tightness/dispersion of the clumps is indeed an important issue which would be critical to examine in detail since it will definitely effect the practical efficiency. I’m actually less worried about size and mass distribution than I am the velocity distribution. Even though I talk about the ‘stationary’ ISM, it’s only the averaged particle motion that would be in any sense stationary. The individual particles will be zooming around with velocities corresponding to the ISM temperature – resulting in the same clump spreading that you note. The reason I’m less worried about the mass dispersion is because the ISM is so hydrogen and helium heavy. Something like ~91% of the atoms are hydrogen, and 8.9% helium. So at most there’s only 3 charge/mass ratios for ions we would need to worry about (1 proton, 2 protons 2 neutrons, and 2 protons 2 neutrons 1 electron). We could either attempt to tune the oscillation cycle to take advantage of all three charge/mass groups, or just ignore everything but the ionized hydrogen and take the minor hit to efficiency. The additional 0.1% of ions which are heavier can be safely ignored without missing out on any significant reaction mass.
Obviously a very, very complicated subject, but it seems to boil down to the concept of “living off the land” which is a highly desirable state of affairs from the standpoint of needing and utilizing whatever’s available for your propulsion needs.
This reminds me of James Woodward’s epiphany that arose as a teenager when he watched the movie “Forbidden Planet” and he became motivated to devise a propulsion system which dependent upon back reaction from as he called it ‘Machs principal’ utilizing space-time as a type of reaction mass. I didn’t read the paper yet, but I intend to as it is fairly complex, but the immediate sense I get from scanning it is it utilizes the interstellar wind to catch a type of sail as a propulsive mechanism.
A lot of the “land” out there consists of the cold temperatures that fill space, mostly CMB remnant radiation, as well as other light. The ability to absorb and emit that medium, i.e., “pump” it, perhaps with metamaterial waveguides, is key to progressing with propellantless interstellar travel, in my opinion.
10MW is indeed a very modest power consumption. I know this defeats the elegance of “propelentlessness” in the strictest sense, but a tiny, efficient onboard fission plant could generate 10MW while using up very little fuel. One advantage is that the probe arrives with a functioning reactor, which would serve it well to power the declaration and exploration portions of its mission. Tiny fission reactors don’t need to be heavy when you don’t care about shielding…
Hi Paul & Drew,
Fascinating concept for the “slow and steady” class of interstellar propulsion. I’d like to see some hard figures on the advantage over a laser-powered interstellar rocket – an advanced ion-drive powered at the 4 kW/kg level would get similar performance for a 300 year Centauri mission.
As for the truism that Project Orion was interstellar capable, it wasn’t. People repeat this half-truth because they’ve heard mangled descriptions of Freeman Dyson’s 1968 thought experiment on a *pure fusion* “Orion” style rocket. The technology for such *pure deuterium fusion devices* didn’t exist then and still doesn’t exist now.
Do you have the numbers for that? As the ion engine uses a propellant, even if you give it the outrageous Isp of 100,000, I get a mass ratio of 3 million to reach 0.05 c.
0.05c = 15,000 km/s = 15E6 m/s
15E6 = Isp x g * ln(Mo/M1)
e^(1.5E6 /Isp) = Mo/M1 [ Assume g = 10 for round figures)
e^15 = M0/M1 [ Assume Isp = 100,000s ]
Mo/M1 ~= 3 million.
More realistic values for ion engine Isp (< 10,000s) give vastly higher mass ratios.
Is your specific power 4KW/Kg giving you the needed Isp of between 1E5 and 1E6 seconds? Is this achievable?
If you are using the ISM as the source of ions, didn't Andrews and Zubrin show this wouldn't work as the magnetic scoops would cause more drag than the thrust?
Hi Alex,
Love that you check my figures. However I was referring to the worked example from Dr Brisbin’s article which flies to Alpha Centauri in 300 years – a somewhat lower delta-vee requirement. As for the limits of ion-drives, I refer you to the Bond & Martin article “Ultimate performance and mission capabilities of advanced
ion thrusters” which describes a similar mission to the above.
The relationship between Power, Time and Distance is straightforward: Power is proportional to Distance^(2)/Time^(3). Meaning that for a flight to Alpha Centauri, if it takes a jet-power of 90 kW/kg to do the flight in 100 years, then it takes ~3.33 kW/kg to do it in 300. I rounded up to account for inefficiencies.
The performance of the system described in the paper is very advanced. The Isp of the ion engine is 400,000 s! This is between 1 and 2 orders of magnitude greater than any existing ion engine, but also with a concomitantly much higher performance power supply.
The reference mission is for a flyby with a 12:1 mass ratio. If the craft were to also slow down to orbit the target world, that would mean a 144:1 mass ratio, dropping the payload to just 8 tons from the initial 100. If such a performance could be achieved, then I think this would make an excellent reference mission, with enough payload mass to do real science and send back data, including those all important images.
However, this later paper “Fearn, D. (2003). The Future Development of Gridded Ion Engines. 39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. doi:10.2514/6.2003-4714 ” suggests an upper limit of Isp at 150,000s, which would result in a far higher mass ratio for a craft. I calculate a flyby mass ratio of 754 rather than 12. Deceleration to 0 km/s would then require a mass ratio of not 144, but rather over 500,000 (leaving a science payload of just 16 g). Neither seems feasible if Fearn’s paper is correct about the upper bounds of Isp.
Hi Alex
I’m a bit more agnostic about the specifics of the ion drive. Strictly speaking, Fearn is discussing the Dual-Stage 4-Grid system in those papers and runs into specific issues of that design concept. My original point in response to Dr Brisbin’s concept, is that beamed power to an electric rocket would perform as well. Thus what’s the advantage of the SWIMMER?
Conceptually, any vehicle that can escape the “tyranny of the rocket equation” is going to be attractive at least in some applications, both in the solar system and for interstellar travel. It took a lot of infrastructure and logistics for coal fired steam ships to displace sailing ships, or gasoline autos to replace horses. Range limitations of the technology were clear.
For an ion engine to have the needed velocity for interstellar travel the Isp must be high enough to allow for a reasonable mass ratio. If it cannot be achieved, that would disqualify it for any but extremely long duration missions, such as powering world ships, or million year seed ship programs.
Apart from early solar sail experiments, we have no non-rocket technology that is available to navigate the solar system, let alone the much harder challenge of interstellar flight.
I want to make one final point about big, super-advanced technology ships that require huge resources. The JBIS Daedalus fusion rocket is an example. Unless we can find a way to transition beyond a K I civilization, I do not think we will ever have a large enough global economy to afford to build such machines. We are reaching [have reached/exceeded?] the limits of an Earth based economy. I fully expect growth to slow down, perhaps eventually to long term historic levels of a fraction of 1% per year. Any possible starship will need to be affordable within such an economy unless we can expand our civilization and economy beyond Earth. We can certainly think big, but I fear they will remain thought experiments and paper exercises only. Even a device like a SWIMMER (assuming it would work) might be too large a project, although I could see it being largely constructed by robots in space. Contrast that with a Breakthrough Starshot (again, if it works) that is affordable as long as the laser array is terrestrial. A key driver is driving down the cost of access to space, to least airfreight prices. Add in really good teleoperated robots to allow humans to work as well remotely as in situ, and economic expansion beyond Earth might be a real possibility, and with it the eventual growth needed to build big, rocket starships. In the meantime, I will place my bets with small, elegant machines that work more like tiny sailing ships, rather than brute force craft that are more like big steamships.
Very nice idea! Do you plan to do more complex computer simulations? That would be ideal for a NIAC proposal.
To those of us insufficiently schooled in mathematics and physics, such devices may seem to be excessively complex but if they do work, more power to the designers!
If we shed such a wire in flight, and it curls up over time – do we get a ca. 100 m scale, very low density object, of which there must be very many? In other words, an ‘Oumuamua? ;) Ok, ok, I stop here to say that this is a very interesting idea!
Another reference:
Optimized trajectories to the nearest stars using lightweight high-velocity photon sails
HELLER R., HIPPKE M. & KERVELLA P.
2017 | Astron. J., 154, 115
https://arxiv.org/abs/1704.03871
Incidentally, the Bond & Martin Ultimate Ion Drive paper is available from the Electric Propulsion Society Archives here: ULTIMATE PERFORMANCE LIMITS AND MISSION CAPABILITIES OF ADVANCED ION THRUSTERS
“… The ion clump that was formed in front of the plate will be attracted to the negative front layer, pulling the spacecraft forward. As the clump approaches the pusher plate, the potential difference is turned off and the clump is allowed to coast through the plate to the other side. In the final “push” stage the same potential difference is applied and the clump is further pushed backwards by the positive back layer of the pusher plate. ”
“… In a real three dimensional case, there will also be loss of efficiency due to particles which do not interact perfectly in one dimension, but instead are pushed off to the side as they pass by the charged wires. Furthermore, this qualitative conceptual analysis does not account for the self influencing behavior of plasmas. ”
We as seeing that the instability of plasmas has been a major roadblock at this point to being able to achieve thermonuclear fusion here on earth. So the question remains, is that a mass of positive plasma will it really be stable during the drift phase, as well as the energized phase between the two oscillating potentials of the wire grids that make up the impulse unit of the craft ?
First felt some skepticism but then seen the numbers and realized that they are good. It still falls within the range of velocities attainable with fission/fusion powered ships, but it’s much easier to test in flight. Also I wonder, can this be used in our own ionosphere to accelerate beam-riding spacecrafts to orbital velocities?
Hi folks, I very much appreciate all the thoughtful comments! There have been a few well-deserved criticisms related to the highly-idealized way I treat the efficiency of such a system. These points are well taken. It is notoriously difficult to get plasmas to do what you want, so the ultimate efficiency in practice may be nowhere near the idealized version. Is it a factor of two worse? Or two hundred? I can’t say right now. I did make some initial attempts to learn about modeling plasmas with particle-in-cell techniques, but I learned quickly that it would take more resources (both time-wise, and perhaps computer-wise) than I had on hand to do so very well. At the moment I don’t have much time to devote to this, but if anyone else is interested and happens to either be an expert in particle-in-cell modeling, or has a nice plasma laboratory, then some further investigation would be quite interesting!
Nonetheless, I think these idealizations are still interesting and useful. They establish that space travel by pushing off the surrounding medium is possible, and they set a limit on what is realistic. In this case we have a limit on what the best possible case is for a spacecraft exchanging momentum with its diffuse surroundings – no spacecraft designed to push off its surroundings can do better without breaking a fundamental conservation law.
The inhabitants of Sigma Draconis 6 developed FTL ion propulsion ages ago…
https://memory-alpha.fandom.com/wiki/Ion_propulsion
Makes one wonder about multimillion or billion year old civilizations and the Fermi Paradox:
Would they deign to grace us with so much as a most minimal of acknowledgements? And…
Would their activities so minimally disrupt matter & energy as to be virtually undetectable to us?
We could be in the middle of a Kardashev Type 3 civilization that spans the Milky Way galaxy and wouldn’t even know it. Not only because we are pretty clueless on these things, but because many would also be very skeptical of the possibility. Not without reason, of course, but what is reason when it comes to a highly advanced alien society?
http://www.projectrho.com/public_html/rocket/aliencontact.php#aliencontact
Religious people make that argument for their God. SETI people make an associated argument that assumes at least one other civ exists even as more detection effort fails to turn up anything.
Hmm also I might have a case of religion then.
?(?????)???
Since even I do assume the existence of other civ’s, but with the caveat that we might not be lucky to be around at the same time. =)
@Robin Datta: Million or billion year old civ’s could exist, but only on condition they would be the ‘sit at home type’ meaning their home planet or found in one or a few planetary systems and not be superciv’s.
It’s a big universe, it might have happened somewhere, and they could indeed have used propellantless sails that carried seeding equipment – meaning no representative was transported in person. Only genetic code and machinery to build a base/worldhouse or any scifi solution of your personal flavour. ;)