Moore’s Law, first stated all the way back in 1965, came out of Gordon Moore’s observation that the number of transistors per silicon chip was doubling every year (it would later be revised to doubling every 18-24 months). While it’s been cited countless times to explain our exponential growth in computation, Greg Laughlin, Fred Adams and team, whose work we discussed in the last post, focus not on Moore’ Law but a less publicly visible statement known as Landauer’s Principle. Drawing from Rolf Landauer’s work at IBM, the 1961 equation defines the lower limits for energy consumption in computation.
You can find the equation here, or in the Laughlin/Adams paper cited below, where the authors note that for an operating temperature of 300 K (a fine summer day on Earth), the maximum efficiency of bit operations per erg is 3.5 x 1013. As we saw in the last post, a computational energy crisis emerges when exponentially increasing power requirements for computing exceed the total power input to our planet. Given current computational growth, the saturation point is on the order of a century away.
Thus Landauer’s limit becomes a tool for predicting a problem ahead, given the linkage between computation and economic and technological growth. The working paper that Laughlin and Adams produced looks at the numbers in terms of current computational throughput and sketches out a problem that a culture deeply reliant on computation must overcome. How might civilizations far more advanced than our own go about satisfying their own energy needs?
Into the Clouds
We’re familiar with Freeman Dyson’s interest in enclosing stars with technologies that can exploit the great bulk of their energy output, with the result that there is little to mark their location to distant astronomers other than an infrared signature. Searches for such megastructures have already been made, but thus far with no detections. Laughlin and Adams ponder exploiting the winds generated by Asymptotic Giant Branch stars, which might be tapped to produce what they call a ‘dynamical computer.’ Here again there is an infrared signature.
Let’s see what they have in mind:
In this scenario, the central AGB star provides the energy, the raw material (in the form of carbon-rich macromolecules and silicate-rich dust), and places the material in the proper location. The dust grains condense within the outflow from the AGB star and are composed of both graphite and silicates (Draine and Lee 1984), and are thus useful materials for the catalyzed assembly of computational components (in the form of nanomolecular devices communicating wirelessly at frequencies (e.g. sub-mm) where absorption is negligible in comparison to required path lengths.
What we get is a computational device surrounding the AGB star that is roughly the size of our Solar System. In terms of observational signatures, it would be detectable as a blackbody with temperature in the range of 100 K. It’s important to realize that in natural astrophysical systems, objects with these temperatures show a spectral energy distribution that, the authors note, is much wider than a blackbody. The paper cites molecular clouds and protostellar envelopes as examples; these should be readily distinguishable from what the authors call Black Clouds of computation.
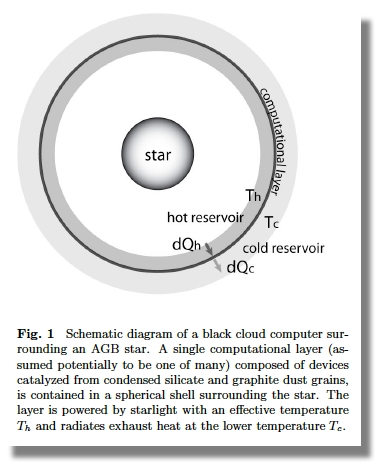
It seems odd to call this structure a ‘device,’ but that is how Laughlin and Adams envision it. We’re dealing with computational layers in the form of radial shells within the cloud of dust being produced by the AGB star in its relatively short lifetime. It is a cloud in an environment that subjects it to the laws of hydrodynamics, which the paper tackles by way of characterizing its operations. The computer, in order to function, has to be able to communicate with itself via operations that the authors assume occur at the speed of light. Its calculated minimum temperature predicts an optimal radial size of 220 AU, an astronomical computing engine.
And what a device it is. The maximum computational rate works out to 3 x 1050 bits s-1 for a single AGB star. That rate is slowed by considerations of entropy and rate of communication, but we can optimize the structure at the above size constraint and a temperature between 150 and 200 K, with a mass roughly comparable to that of the Earth. This is a device that is in need of refurbishment on a regular timescale because it is dependent upon the outflow from the star. The authors calculate that the computational structure would need to be rebuilt on a timescale of 300 years, comparable to infrastructure timescales on Earth.
Thus we have what Laughlin, in a related blog post, describes as “a dynamically evolving wind-like structure that carries out computation.” And as he goes on to note, AGB stars in their pre-planetary nebula phase have lifetimes on the order of 10,000 years, during which time they produce vast amounts of graphene suitable for use in computation, with photospheres not far off room temperature on Earth. Finding such a renewable megastructure in astronomical data could be approached by consulting the WISE source catalog with its 563,921,584 objects. A number of candidates are identified in the paper, along with metrics for their analysis.
These types of structures would appear from the outside as luminous astrophysical sources, where the spectral energy distributions have a nearly blackbody form with effective temperature T ? 150 ? 200 K. Astronomical objects with these properties are readily observable within the Galaxy. Current infrared surveys (the WISE Mission) include about 200 candidate objects with these basic characteristics…
And a second method of detection, looking for nano-scale hardware in meteorites, is rather fascinating:
Carbonaceous chondrites (Mason 1963) preserve unaltered source material that predates the solar system, much of which was ejected by carbon stars (Ott 1993). Many unusual materials have been identified within carbonaceous chondrites, including, for example, nucleobases, the informational sub-units of RNA and DNA (see Nuevo et al. 2014). Most carbonaceous chondrites have been subject to processing, including thermal metamorphism and aqueous alteration (McSween 1979). Graphite and highly aromatic material survives to higher temperatures, however, maintaining structure when heated transiently to temperatures of order, T ? 700K (Pearson et al. 2006). It would thus potentially be of interest to analyze carbonaceous chondrites to check for the presence of (for example) devices resembling carbon nanotube field-effect transistors (Shulakar, et al. 2013).
Meanwhile, Back in 2021
But back to the opening issue, the crisis posited by the rate of increase in computation vs. the energy available to our society. Should we tie Earth’s future economic growth to computation? Will a culture invariably find ways to produce the needed computational energies, or are other growth paradigms possible? Or is growth itself a problem that has to be surmounted?
At the present, the growth of computation is fundamentally tied to the growth of the economy as a whole. Barring the near-term development of practical ireversible computing (see, e.g., Frank 2018), forthcoming computational energy crisis can be avoided in two ways. One alternative involves transition to another economic model, in contrast to the current regime of information-driven growth, so that computational demand need not grow exponentially in order to support the economy. The other option is for the economy as a whole to cease its exponential growth. Both alternatives involve a profound departure from the current economic paradigm.
We can wonder as well whether what many are already seeing as the slowdown of Moore’s Law will lead to new forms of exponential growth via quantum computing, carbon nanotube transistors or other emerging technologies. One thing is for sure: Our planet is not at the technological level to exploit the kind of megastructures that Freeman Dyson and Greg Laughlin have been writing about, so whatever computational crisis we face is one we’ll have to surmount without astronomical clouds. Is this an aspect of the L term in Drake’s famous equation? It referred to the lifetime of technological civilizations, and on this matter we have no data at all.
The working paper is Laughlin et al., “On the Energetics of Large-Scale Computation using Astronomical Resources.” Full text. Laughlin also writes about the concept on his oklo.org site.



The assumption of the inviolability of the Landauer Limit may not be absolute as it assumes irreversible computation and entropy increases. This may be making assumptions that are not valid.
Landauer’s Principle
Having said that, IT now consumes 10% of the global electrical energy supply:
Big question: what are the processes to organize such an enormous “Black Cloud” to do one’s bidding? And to maintain it in that state?
There are instances in nature where chaos leads to self-organization, but can such a process be direted towards a specific organized state that meets one’s ends?
Time for the folks at Centauri Dreams to go on high alert, because Alpha Centauri C1 is here! Maybe. https://www.nature.com/articles/s41467-021-21176-6 https://www.dailymail.co.uk/sciencetech/article-9242737/Potential-exoplanet-harbor-life-noise-canceling-headphones-method.html
Direct imaging from Earth’s surface. Might be the size of Neptune, might be at around 1 AU … no word on moons, atmospheres, flora, travel agents. These are still early days.
This doesn’t sound like a long term investment. Perhaps it would be ideal for research or manufacturing projects where the demand for computing is short lived.
Great pair of articles, thank you Paul Gilster. Some thoughts.
Machine embodied minds may seek the security of stand alone devises. Autonomy is more difficult to maintain in a virtual space where everything is starkly similar and intimately connected. Would humans ever come close if touching risked becoming the same person or sharing everything? The energy cost of Ai evolution may be high.
With the possibility of astronomical computers we must consider the existence of K1-K3 persons. The probability of convergence on a singular mind may so high, astronomical computers aren’t built unless that’s the goal. This method may be a way to build a kill switch into an inherently dangerous devise.
The prospect of competition between humans and other machine embodied minds is real. Hopefully, there are scenarios where everyone flourishes. Everyone is a machine embodied mind. Other machine embodied minds may flourish in space. Retreat is a successful strategy, perhaps optimal. A risk remains for planet natural people. Joining a successful, true space faring people would be the equivalent of becoming an angel. Who would choose death? A planet natural people may sublimate into space.
If other machine embodied minds are inevitable, then perhaps planet natural people survive by embracing exchange and cooperation. Trading according to comparative advantage will reinforce the identity found in being a planet natural mind. The social and economic landscape is mind boggling! I am not just talking about trading cultural artifacts. Weird math with no bearing on reality may be a powerful tool for building machine qualia.
Biotechnology could open alternatives for manufacturing’s and computing’s demand on electricity. A modern factory could be reproduced in flesh. That flesh could be fed a renewable or waste material. Biological computing has proven itself. The production of electricity also has a waste heat dilemma. I don’t know how well biotechnology copes with this dilemma. The evolution of biotech is also reliant on general computing.
In the short term, we will have to adapt. Software has gotten fat and lazy riding cheap computing power increases. The overall economy can be more effective in how it uses computing power. The toaster shouldn’t have a brain. Applied democratically, computing can overcome economic hurdles. Realistically, we will see a lot of cloud imperialism. There are always promises from quantum computing and hopefully, we soon see q-bit numbers and error correction pass a practical threshold. The many properties of carbon nanotech, especially low cost superconductivity, may unlock a new dimension of computing that demands a new growth model.
I thought including the computing power of Earth life was insightful. It built the perspective of an ET observer. Earth life would be an interesting computer to query. It is a qualia rich system.
Douglas Adams got there first half a century ago, with Earth built as the ultimate computer to answer what the ultimate question is (Deep Thought had previously answered that the answer to the ultimate question was “42”).
FEBRUARY 11, 2021
To find an extraterrestrial civilization, pollution could be the solution, NASA study suggests
by Bill Steigerwald, NASA
https://phys.org/news/2021-02-vaporised-crusts-earth-like-planets-dying.html
At least they aren’t just thinking of SETI in terms of radio waves only any more.
It’s an interesting idea, but it must remain science fiction because in order for silicon to be a semi conductor it has to be “doped” with another metal like antimony or boron to give it extra electrons.
The argument about the energy needed for computation and AI is still interesting. We now have quantum computers to do some calculations much faster but they take energy because they have to be cold. If we could make them without having to get cold like a superconducting fermion condensate they would take less energy. Progress and innovation should result in making computers which are more efficient or use less energy which would include AI. Also new power sources like fusion eventually will increase power output with more efficiency.
FEBRUARY 11, 2021
Vaporised crusts of Earth-like planets found in dying stars
by University of Warwick
https://phys.org/news/2021-02-vaporised-crusts-earth-like-planets-dying.html
Dyson swarm architecture depends on many currently unknown things, like the exact optimums for computation and communication processes in such environments. If the middle-to-near IR is the best band, because of greatest bandwidth, the directed communication ability, and the photon energy that matches molecular transitions in the nanostructures that encode information, they would be more compact.
The concept is fascinating. A Dyson swarm around G star can simulate billions of billions of human civilizations where noone would notice any difference with the real world, if estimates in Charles Stross’ Accelerando are correct (as I remember, the throughput was off by some oomags, but this does not matter). Still countless if all biosphere throughput is simulated, down to DNA replication and all neural processing on a planet.
But I doubt they stay around AGB stars. Dyson-swarm technology enables Nicoll-Dyson beams, which can accelerate impressive chunks of computronium to relativistic speeds while powering them all the way to the other suitable star. “Accelerando” assumes they all stay at home, but it was it’s plot. In reality the opposite is likely true. Seeds powered up by NDBs can travel between the stars with ordinary inhabitants of simulated worlds not even noticing a difference. Maybe even the intergalactic travel (say, to the black hole in M87) is possible.
PS a quick calculation on my way through snows. A Dyson swarm around an O-type star could easily divert a hundred of solar luminosities to power and accelerate a seed with a Nicoll-Dyson beam. Assuming conservative computational efficiency of 1000 eV per elementary operation, that’s 10^44 EOPS of computation, enough to simulate 10^27 humans by Accelerando estimates. The beam gives 10^20 newtons of pressure, which is enough to accelerate the whole of Earth at 0.1 mm/s^2. (not counting the Death Star effect) The 1 m/s^2 acceleration, giving half-lightspeed in five years, is achieved for a seed with mass of Enceladus, capable of storing more than trillion of trillion of exabytes (2.5*10^44 bytes at 1000 atoms per bit and mean atomic weight of 28). The sail for 1 MW/m^2 would be about 1 AU in width, but hey, were are talking about a Dyson swarm builders. Advanced dielectric sail can take much more, but photoelectric converters on it’s surface – probably not. If computronium is evenly distributed around the sail, there will be no unsurmountable stress on it’s fabric.
Would be visible by scattered light from hundreds of parsecs, but not in the other side of galaxy. Possibly could be identified by LSST as an extremely high proper motion source.
The deceleration at target would be difficult by our measures, but possibly not with Dyson-swarm-class technology. One way is to use reflected light from separated sail, as was mentioned on Centauri Dreams before. Microarcsecond collimation and steering is not a problem with apertures of that scale. If magnetobraking is used, by orbit-wide superconducting loops supported by adamantium strings, then ultra-low-frequency synchrotron signal will be detectable from great distance, but with short duration.
Not many things are as fascinating as imagining K2-scale activities!
You mention the WISE source catalog has over half a billion objects.
That reminds me, I’ve been wondering…about the claim there are 100 billion galaxies in the universe. How many have we actually cataloged? How much is that number just a wild guess? Thanks.