As we follow the progress of the James Webb Space Telescope through performance tests in preparation for launch, Robert Zubrin has been thinking of far larger instruments. The president of Pioneer Astronautics and founder of the Mars Society thinks we can create telescopes of extremely large aperture — and sharply lower cost — by using the physics of spinning gossamer membranes, a method suitable for early testing as a CubeSat demonstration mission. In today’s essay, Dr. Zubrin explains the concept and considers how best to deploy next generation space telescopes reaching apertures as large as 1000 meters. We can’t know what new phenomena such an instrument would find, but the Enormous Space Telescope fits the theme of breakthrough discovery outlined in his latest book, The Case for Space: How the Revolution in Spaceflight Opens Up a Future of Limitless Possibility (Prometheus, 2020).
by Robert Zubrin
Abstract
This paper presents a method for creating Enormous Space Telescopes (ESTs). The EST employs a hoop to deploy a slack reflector membrane, such as solar sail material or radio dish. When the EST is simultaneously rotated around its center and accelerated along its axis of rotation, the membrane will assume a parabolic shape, thereby creating a reflector for a very large aperture telescope. The EST reflector can be accelerated along its linear axis by tethering its deployment hoop to a tug spacecraft. The tug can exert force on the hoop several methods, including direct thrust, centrifugal rotation of the tethered tug-reflector assembly, or by lowering the reflector from a high altitude balloon or more massive tug positioned in a higher orbit. A force equivalent to linear acceleration can also be generated to shape an EST without a tug using electrostatic means. ESTs can be used for astronomy across a wide spectrum of frequencies, ranging from the ultraviolet, through optical and infrared, down to radio. A demonstration EST with an aperture larger than the Webb Space Telescope could be flown on a CubeSat mission in low Earth orbit. ESTs with apertures of hundreds of meters could be delivered to heliocentric space in single flights of existing launch vehicles.
Background

There is no better place to do astronomy than space. Therefore, since the dawn of the space age, it has been the ardent ambition of astronomers to place ever more capable telescopes there. The largest such operational instrument, the 2.4 m diameter aperture Hubble Space Telescope, has benefitted from its location above the Earth’s atmosphere to make many great discoveries, and astronomers hold high hopes for more breakthroughs from the long-awaited 6.5 m diameter Webb Space Telescope. As the light gathering power of a telescope increases with the square of their aperture, still larger space telescopes are greatly to be desired. However, as the cost (>$10 billion) and quarter century long development schedule of the Webb telescope have demonstrated, new techniques will be required if construction of much larger observatories is to be made practical. This is the purpose of the Enormous Space Telescope (EST) concept.
The Enormous Space Telescope (EST)
The EST exploits the principle that if a flexible material subject to a linear acceleration is spun, the balance of linear acceleration and centrifugal acceleration forces will shape the material into a parabolic geometry. This technique has been used on Earth to spin cast liquid glass into parabolic dishes for use in telescopes up to several meters in diameter. The EST can employ similar physics with a properly tailored sheet of gossamer material in space to create parabolic reflector dishes with dimensions of hundreds of meters while keeping system masses well within existing launch vehicle limits.
In order to understand how the EST works, let us start by considering it in its smallest and possibly initial form, as a CubeSat demonstration mission. Consider a 13 kg, 12U CubeSat in a circular orbit 400 km above Earth. A one kilometer long tether is extended down from the satellite, and used to suspend a 13 m diameter (twice that of Webb) hoop, whose central axis aligns with the tether. Lines from the circumference of the hoop attach to the tether by a frictionless magnetic bearing, allowing the hoop to rotate freely. The interior of the hoop contains a slack solar sail material, properly tailored to accept a parabolic shape without folds, which is attached to the hoop like the skin of a slack-topped drum. Aluminized balloon film can be used to create solar sail material with a mass density of 6 grams/m2. Taking the hoop mass into account, we will assume 10 gm/m2 as the net mass density for our hoop/film combination, resulting in a mass estimate of 1.3 kg for that subsystem.
At an altitude of 400 km, the CubeSat will be moving with a velocity of 7668.63 m/s, generating a centrifugal acceleration of 8.6762 m/s2, exactly matching the Earth’s gravitational acceleration at that altitude. The reflector, however, hanging 1 km below the CubeSat will only be moving at 7667.50 km/s, generating a centrifugal acceleration of 8.675 m/s2. The Earth’s gravitational acceleration at that altitude will be 8.679 m/s. Thus the hoop will experience a downward acceleration of 0.004 m/s2, or 0.4 milliGees. This will make the sail film in the hoop sag. But if we rotate the hoop with an edge velocity of 0.1 m/s, the film material will also experience an outward acceleration, ranging from 0 at its center to 0.0015 m/s2 at its edge. Taken in combination with the linear acceleration, this will shape the film into a perfect parabola.

Fig. 1 An EST suspended by a tether in LEO. The telescope parabolic dish is spinning around the axis of the tether. Earth (down) is on the right.
This little demonstration EST, with a total mass less than 20 kg, including optics that would be positioned along or suspended from the tether at the parabola focal point, would have four times the light gathering capacity of Webb (about thirty times that of Hubble), while costing on the order of 1/1000th as much.
An even cheaper flight demonstration could be done suspending an EST from a high altitude balloon. Since a balloon moves with the wind, the payload would feel no wind. At 100,000 ft it would be above 99% of Earth’s atmosphere. A triangle of long spars could be employed with a balloon attached to each vertex, to keep the balloons out of the field of view of the telescope.
Such systems would have limitations, since they would be constantly pointing directly away from the center of the Earth. But we can do better.
Let us therefore scale our unit up in diameter by a factor of ten, to a 130 m diameter reflector dish, increasing the mass of the hoop, the optics and spacecraft by a factor of 100. It would still be a quite manageable mass though, about 2000 kg, easily launchable into interplanetary space by a Falcon 9 medium lift booster. In this case. there would be no gravity gradient available to stretch the tether. So we need to use an alternative technique.
One approach might be to spin the hoop around the spacecraft, in the manner of a tethered artificial gravity system, having a second hoop counter-rotating along with the one suspending the dish in order to neutralize gyroscopic effects. But such a system would still need to constantly change its pointing direction, making long duration exposures impossible.
Tugs for ESTs
A more effective approach would be to simply employ a spacecraft as a tug. Sunlight has a pressure of 9 micronewtons per square meter, which would add up to 0.12 Newtons over the whole body of the 130 m diameter sail. If that were the only linear acceleration of the sail, it would shape it into a parabolic reflector with its concave side pointing towards the Sun. As we want to be able to point the telescope the other way, we need to generate more thrust than that. This could be done using either electric propulsion or larger solar sails with a lower mass density then the hoop, or magnetic or electric sails, pulling its tether outward from the Sun.
Let us first consider electric propulsion. If we had an 70% efficient ion engine using argon propellant and a Isp of 7000 s, 50 kWe would be required to produce 1 N of thrust. Assuming a typical solar electric propulsion system mass to power ratio of 20 kg/kWe, that would require 1000 kg. The tug would thus accelerate at a rate of 0.001 m/s2. If the reflector was made of sail material with the minimum mass density of 6 gm/m2, its material would self-accelerate away from the Sun with an acceleration of 9e-6/0.006 =0.0015 m/s2, which is greater than the self-acceleration of the tug, and therefore unsatisfactory. However, the remedy for this is simple: just make the reflector material much thicker. For example, if we tripled its thickness to 18 gm/m2, its self-acceleration would only be 0.0005 m/s2, i.e. half that of the tug. So it would lag behind the tug and the net pull on it of 0.0005 m/s2 would make its center sag back towards the Sun. If we then set it spinning with a velocity of 0.1 m/s at its edge, an edge centrifugal acceleration of 0.00015 m/s2 would be created, shaping it into a 130 m diameter parabolic dish.

Fig. 2 Electric Propulsion tug pulling on an EST.
Operating at 1 N thrust, the thruster would consume 0.014 gm/s of propellant, or about 1.2 kg per day of thrusting (i.e. observing time). Thrust and thus propellant requirements would drop if the telescope were positioned further out in the solar system, since solar light pressure would drop as the inverse square of the telescope’s distance from the Sun. Thus, for example at 3.1 AU, it would only need to use 0.12 kg/day of propellant to generate adequate acceleration.
We could also use solar sails as tugs. In this case no propellant would be needed. Positioning the tug behind the EST would allow it to eclipse solar pressure, as shown if Fig. 3. If the tug is pulling the EST, making tug acceleration greater than reflector material self-acceleration could be assured simply by having the tug sails be larger than the reflector sail, and using a heavy gauge material for the reflector sail.
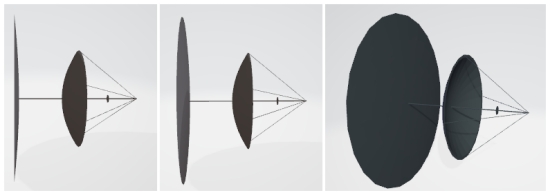
Fig. 3 Using solar sail tugs to accelerate an EST, by pushing from behind. The EST spins around the central axis. The Sun is on the left. An alternative design would send the mast through the sunward pusher sail, allowing it to deliver its thrust to the base of the mast by a set of shrouds.
A pusher sail telescope would need to point (generally, but not necessarily exactly) outward from the Sun all the time. However if a nuclear electric tug were used, and the telescope were positioned in the shadow of a planet, sunlight impinging on the rear side of the reflector would not be an issue and the telescope could be pointed in any direction.
In the case of radio telescopes, all of this becomes much easier, as there would be no solar light pressure on the rear face of the dish. In that case any kind of tug – solar electric, nuclear electric, or solar sail- could be used, with the EST pointable in any direction simply by maneuvering the tug. The amount of acceleration required from the tug could also be much less.
The Electrostatic EST
An alternative to physical acceleration to impose linear force on the dish is to use electrostatic attraction, In this case the reflector sail would be charged one way, while another sail positioned behind it and held off at a distance by a structural system would be given an opposite charge. The sails would thus attract each other, much as if by gravity, and when the assembly was spun up, both sails would assume parabolic shapes, with their concave sides pointing in opposite directions.
Let us consider the case of two 50 m radius dishes held 25 m apart by structure, with a potential difference between the two of 10 kV, creating a field of 400 volts/m. From electrostatics we have EA = Q/?, so Q, the charge on each dish will be given by Q=(400)(7854 m2)(8.85e-12) = 2.8e-5 coulombs. The electrostatic force on each sail will be given by F=QE, so the total electrostatic force between the sails will be F=400(2.8e-5) = 0.0112 N. Assuming the sail materials have a mass density of 6 gm/m2, this will result in a self-acceleration each sail towards the other of 0.0112/(0,006)(7854) = 0.00024 m/s2. It may be observed that the field will actually be greater near the center because the dishes would sag towards each other. This, however, could be compensated for by varying the thickness of the sail material, making it thicker towards the center and thinner towards the edge, thereby keeping the linear self-acceleration of the two sails towards each other equal over their entire surfaces.
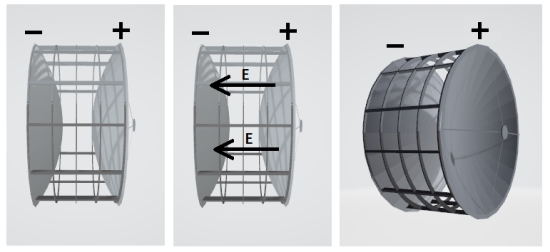
Fig. 4. An Electrostatic EST. The sails have opposite charges and are held separate from each other by a compressive structure. The mutual attraction of the sails can substitute for linear acceleration of the system
Size Limits of ESTs
There does not seem to be any theoretical limit to the potential size of an EST. However, as we have seen, using current materials, the mass required the create an EST system goes approximately as:
![]()
Where M is the EST system mass in kilograms and R is the aperture radius in meters. Thus our 6.5 m radius EST demo unit has an estimated mass, including its associated spacecraft, on the order of 20 kg, while our 65 m radius operational EST would be expected to have a mass on the order of 2000 kg.
Currently the largest operational launch vehicle is the Falcon Heavy, with a capability of about 60,000 kg to low Earth orbit (LEO). More powerful vehicles, including the NASA SLS and the SpaceX Starship system are expected to become operational within the next few years, with capabilities of up to 120,000 kilograms to LEO. Since an EST tug could propel itself out of LEO and into heliocentric space, this may also be taken as the limit of the size of an EST system, deliverable into space with a single launch. If we plus 120,000 kg into equation (1), we find that a practical size limit for relatively near-term EST systems would be an aperture diameter of about 1000 meters. The discoveries that might be enabled by such systems are beyond reckoning.
Conclusion
We find that the EST concept offers a practical path towards creating space telescopes with capabilities dwarfing conventional systems by many orders of magnitude. We also find that ESTs could be used to create space telescopes with comparable capabilities to conventional systems, but with several orders of magnitude lower cost. Furthermore, the EST concept holds these benefits for space astronomy across a wide range of frequencies, from ultraviolet down to radio. We therefore recommend that the concept be studied further, and that a demonstration mission be flown at an early date.
Acknowledgement; The author wishes to acknowledge the assistance of Heather Rose, who provided the illustrations for this paper.



How the charge non-uniformity is going to be dealt with? If the reflector is conductive, then all charges will rearrange to minimize electrostatic field energy, and this will break force uniformity. If it is insulating, then it will be very difficult to charge it uniformly and then to mitigate charging effects by solar wind. The acceleration towards the target looks much better, but still, it requires equally uniform mass distribution, or there will be at least precession and tracking issues.
Still, since there is no weight in space, shape maintaining is radically simpler than on Earth, and cost per surface follows much less steep power law then here. Past 10000 square meter mark at optical range we’ll have absolutely no choice.
But still I believe the good old Maccone-style reflector fleet is the best design. A formation of free-flying lightweight mirrors aligned to optical precision by laser interferometry, ion drives and piezo-actuators, some of them on the primary reflecting surface, some on the secondary. Extremely scalable, versatile and fault-tolerant. It could start with not much more than a dozen and scaled up to many thousands of them. It could attain virtually any aperture width and focal length. It won’t suffer much if a mirrorsat is killed by a cosmic ray or even a stack of replacement units does not make it in into orbit. It could even split in two or ten smaller telescopes, like formation of drones or a flock of birds, if there is need to watch many targets simultaneously, and then reunite to resume the deep stare. It could expand into exoplanet-resolving-size without consuming much propellant, using the advantage of free flight and uniformity of gravity field at Lagrange points. Of course, there will be second-order diffraction limits – a thousand-kilometer-wide aperture cannot be attained with meter-sized reflectors – and the sparser the aperture, the more imaging artifacts, but still not as hard as the FOCAL telescope. It could live for centuries, being constantly rebuilt and replenished with no downtime at all.
Only the graviscope and maybe terrascope is more beautiful than that.
What about an inflatable lens? Imagine a hula hoop with two films sealed to either surface. One is clear to whatever wavelength you wish. The other film reflects your wavelength of interest. Inject variable amounts of some Helium into the chamber, and you have a variable focal length mirror. No acceleration or spin needed. Now make it any size you want, the limit is tensile strength of the film and how to repair holes. I’ll wear a kilt instead of a tux for the Nobel ceremony, thank you.
Helium is notoriously able to get out of practically anything, think teenager and you have an idea of the enormity of the problem, solve it and you will get the nobel peace prize thrown in !
PS I’ve noticed a confusion only after I hit submit button. Of course, FOCAL is the Maccone design, and nothing could surpass it save for direct travel to the target. I just cannot remember who proposed the sparse-aperture free-flying mirror optical interferometers, nor am able to quick google it now. And there are many different versions, with or without lenses, with more complex or simple geometry. What I describe is something like this, to the right, but with multiple secondary mirrors as well: https://images.app.goo.gl/ZRmvdd5mGKJeXbez7
Antoine Labeyrie and his spherical interferometer ‘hypertelescope’ ?
Terrific write-up of a comparatively simple idea. I would love to know: what could we dream of seeing with a space telescope of 1km aperture? (The preferred answer in the form of “x-by-x-pixel representations of exoplanets Y light-years away”.)
A 1km telescope operating in visible light would have an angular resolution of about 0.1 milliarcsec (~500x better than Hubble). Even the largest suspected exoplanet in angular diameter as seen from Earth (Epsilon Eridani b) is only about 2 pixels across.
Yeah, I don’t think it can compete with SGL for exoplanets. Although if you could make a 1km telescope, you could place it at the SGL & would it offer a modest increase in resolution over a 2m scope? I am told it goes as the square root of the aperture, is this correct?
What about microlensing for exoplanets? Or cosmology work?
The downside of the approach outlined is that the mirror must be under constant rotation and acceleration along the axis. This makes operations difficult.
I suggest a solution to this. Using a UV curable coating on/as the film, the structure will stiffen and set rather like a soap bubble in icy air. Once the film cures under the solar UV, the mirror needs no longer be accelerated along its axis to generate a force, nor would it need to rotate.
Such a stiff, “soap bubble” mirrors could then be pointed with relative ease.
A further wrinkle would be to compensate for any distortions due to imperfect curvature. As a commenter pointed out in an earlier post, it is possible to create a mirror with reflective particles. In this case, the distortion could be detected by shining lasers onto the surface and correcting for any deviation of the reflected beam on the sensor array.
There are other uses for such large, lightweight mirrors. They would make excellent concentrators for solar thermal engines, offering relatively decent Isp with higher thrust. Kraft Ehricke suggested using inflated balloons with half transparent and half mirrored as teh concentrator, but this lightweight, parabolic reflector would be a potentially superior option in terms of mass and focal performance. Using readily available volatiles in space from water, ammonia, even CO2, such propulsion might make cargo shipments around teh solar system relatively inexpensive.
Kraft Ehricke’s balloons would no doubt work, the precision to focus light for energy is perfectly possible, the precision needed for an astronomical mirror is in some doubt but still better than Zubrin’s idea present here.
There’s already many posts on why his proposal will not work that I need not repeat them.
Interesting…would this work in a “statite” configuration? I’m suddenly picturing a solar telescope able to study the Sun in unprecedented detail…
I look forward to seeing a Space Telescope of Enormous size to work with! Please visit my Facebook page to see Space Telescope images that I have worked with.
I don’t do Facebook.
I don’t either. That makes two on earth, so far.
Three.
FaceBook?
Four.
Five.
I don’t like the propulsion. I like a little more thrust and control. I do like the idea, but your mirror is not truly enormous. Maybe make a whole bunch of these mirrors and lock them together to make it bigger.
I still like the JWST better because it is made of many smaller pieces which are easier to launch. I am thinking about maybe a one hundred meter space telescope made of smaller segments. We could build it like wheel space station and even have crew quarter underneath the mirror.
I remember the old interferometer idea. With two JWST’s we could cancel out the light by combining images or maybe four smaller mirrors combined. If we are worried about the cost, then forget it. The grandiosity goes out the window. Think big and think grand. It’s the future so make it good.
I don’t know enough about the suitability of the optics, but distraction Fresnel lenses manufactured by cutting annular rings into an opaque substrate will focus light. The advantage of such lenses is that they are flat and thus can be deployed easily, kept flat by rotation. Whether they are suitable for astronomical purposes, IDK.
Tensioned membrane structures can exhibit a number of elastic instabilities like wrinkles. These instabilities could prevent the structure from attaining a parabolic structure after deployment. Variations in film thickness, temperature, and composition may also cause deviations from a parabolic shape. Electrostatically controlled membranes have been investigated and shown to have some deviation from parabolic: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1050.1730&rep=rep1&type=pdf
The proposed mirror would inevitably suffer from chaotic wavefront aberations due to number of factors. Vibrations and or nonuniform acceleration(due to local variations in solar pressure) will create a disturbances in the reflective plane causing image deterioration.
You’re being exceptionally polite. The entire idea is exceedingly ill considered. Pretty well all the important factors have been passed over in this proposal. I had to laugh at the idea of deploying this thing at 400 km height. It wouldn’t last more than several seconds (during deployment!) before atmospheric drag on this high surface area and low mass object would begin to self destruct.
Deployed edge on would reduce the drag, and may not be important for the demo CubeSat version. The Planetary Society’s solar sail deployed at around 700 km without damage, so raising the deployment altitude is not a showstopper.
Could we not do just as well by using a large crater on the far side of the moon?
How would such a telescope stare at a fixed stop in the sky for long. Even with a 30 day scan of the sky with very limited focus following, it would be useless for astronomy requiring long observation periods. How much of the sky and target tracking was the radio telescope at Arecibo able to do?
Lunar dust is constantly being raised and deposited. How would the mirror be kept clean?
Wherever this mirror is put, it will be subject to micrometeroid impacts that will deform parts of the mirror.
Quite a bit of thought has been put into Andrew’s idea and there are some serious proposals like:
https://www.universetoday.com/148857/a-100-meter-rotating-liquid-mirror-telescope-on-the-moon-yes-please/
Interesting PR fluff. The article reference a PR piece from the McDonald observatory that also uses a misleading title. This in turn references the source arxiv piece with was solely about the requirements for observing distant population III stars. There is a passing reference that a liquid mirror, possibly on the Moon, might theoretically work.
The Area can be kept clean of dust by glassification of the surrounding dust with a wire chargeable mesh imbedded. The moon offers a huge area for mirrors and linking them into one telescope would give us a huge advantage.
> Lunar dust is constantly being raised and deposited. How would the mirror be kept clean?
Considering we are eventually building permanent settlement on the Moon, that becomes less of an issue – maintenance can be done locally by teams living nearby. Shipping the materials, unfortunately, isn’t great – you need to spend fuel to land, something a deep space telescope doesn’t need, but we could send manufacturing equipment and build mirror elements from regolith glass. Being on a settled surface is incredibly handy and the techniques and capabilities developed for it could be used for a lot of other endeavors.
A 2015 PhD thesis for inflated parabolic mirrors for CubeSats:
Inflatable Parabolic Reflectors for Small Satellite Communication
A number of issues were examined. The mirror is not good enough for optical work but is suitable for radio communication.
Other commenters have noted that a reflective film mirror will likely not have the optically correct curvature across its area, reducing the effectiveness of such a mirror. I do think post image correction is possible, but whether it is worth it given the other costs of launch and operation, IDK.
Some modifications to this might be beneficial. For example, make the mirror into an annulus, and provide a much smaller convex mirror not far from its focus to provide a Cassegrain design. Detectors would be at a secondary focus behind the main mirror. For a given mass this could increase resolution at constant light gathering power.
One thing not mentioned is the issue of surface shape accuracy. Typical scopes for light are 1/10 or 1/20 wave accuracy. I doubt that could be achieved with this design. However, with a beam splitter near the final focus as a light diverter to a detector and computer maybe the secondary mirror could be driven as a rubber mirror to correct wavefront errors in the primary. One could also put an occulting disk in the beam to block direct starlight.
Since the secondary mirror is flexible, one might also think about driving it to more specialized aspherical shapes, for example to create a version of a Schmidt camera, with a wide field of view.
One could also think of dispensing with the spin but just stretch the film flat and coat the reflector as a Fresnel Zone plate. All remarks above about the secondary would apply.
The CubeSat demonstration is rotating about the axis of the telescope, but it also would seem due to rotate in time with its revolution around the Earth. Is the demonstration only momentary, or is there a way to deal with the angular momentum issues? (I have to admit some ineptitude with gyroscopes)
I can see this working for light concentration, but I’d have to see some analysis of what the figure would be like for real world levels of film irregularity and vibration, to believe it would work for a telescope.
Could such a thing be built and ‘connected’ to a small asteroid, to use its very low gravity for deployment? It would not need the ion tug for acceleration then.
As an alternative, for very large telescopes, I’d suggest making them out of free floating segments with high precision station keeping. The individual segments would gain economy from mass production, the telescope could be upgraded in area while in use. Likewise, the objective could be free floating, too.
With a sufficiently long focal length compared to the size of the segments, the segments could simply be optical flats, and still have a fractional wavelength figure, further lowering the cost and increasing the versatility, since the focal length could be altered as desired by changing the position of the segments. (Not an idea original to me, of course.)
Reducing station keeping thrust to manageable levels would probably require placing the telescope at a Trojan point, or otherwise distant from any large body, as tidal effects would add up across such a large composite structure otherwise.
And along comes a ton of space junk or an assortment of rocks and gravel from a decomposed meteor.
I am thrilled by the idea, it is practically a disposable scope. Leaving aside the detailed objections, I suspect any wrinkle-induced image distortions could easily be modeled and corrected using image processing, even if they were dynamic.
Alex T alluded to mentioned an inflatable “lens.” Combining that with UV curing and stiffening you could then unzip the lens along its equator, unfold it into position (big arm wave here!), and have two mega Gemini “binocular” mirrors for the launch of one.
Alternatively combining the inflatable to create a framework, with a liquid metal layer that is spun up to produce a smooth parabola is in the literature. https://en.wikipedia.org/wiki/Liquid-mirror_space_telescope
While few ideas are entirely new, Zubrin’s got my heart beating a bit faster!
Zubrin is a brilliant proponent of human space exploration and of the settlement of the solar system and beyond. No one pushes as hard in trying to get humanity to move quickly on these key issues. I am a fan of his 1996 book *Case for Mars* and his 1999 book *Entering Space*. I admire him for founding the Mars Society.
But there’s another side to Zubrin that is hard to mesh with his fervent advocacy of human space settlement. It is laid out in his 2012 book *Merchants of Despair*. There is a huge section of humanity which raises the alarm about the possible demise of the planet and our species due to climate change, overpopulation, resource depletion, industrial expansion – and rightly so per reliable scientific evidence. This is a huge sector of humanity that could be persuaded of the importance of Zubrin’s space settlement goals and become useful allies.
Yet Zubrin calls them antihumanists, merchants of despair, and accuses actors from this sector of humanity of establishing genocidal programs and eugenics campaigns. The solidly established science used to illustrate climate change and justify the sounding of alarms is dismissed as psuedo-science by Zubrin. But Zubrin is the one using psuedo-science to tar real science with the politically charged moniker of psuedo-science.
Publishers Weekly gave this book a positive review. Greg Benford, well respected on these pages, throws his weight behind Zubrin’s views by calling *Merchants of Despair*: “The most devastating account and refutation of antihuman environmentalism ever written.”
I know all about free speech, political choice, etc. I’m a plaintiff’s attorney and I give everyone plenty of room for their views. Zubrin et al. can believe what they wish. What I fear is that with the addictive spector of psuedo-science well-established in their brains, scientists such as Zubrin may find it difficult to effectively use real science at some future time when humanity really needs them to do so.
We need a like button for these discussions.
I have in fact been fully aware of Zubrin’s extreme views since his speech included the words ‘Manifest destiny’ in his Case for Mars presentation.
Where a number of the attendants rightfully reacted since the term is one declaring racial superiority and the basis of a philosophy of settler colonialism and genocide of the native population.
I have rather avoided to make any comment on these matters and stayed on the proposal at hand when Zubrin have been brought there.
But now the genie is out of Pandoras box, and thank you for that.
His book have indeed been used as a political tool, but people who do not only say “psuedo-science” but also yell ‘fake news’ at anything that go against their political agenda.
What is especially hair-raising is that Zubrin do so, as he then completely ignore the fact that every claim made is scrutinized in detail in the usual process of peer-review.
I am not working on environmental matters even less on climate change. Even so I have to take both into account to be able to do my work, or to explain what I encounter. Such as species about to be declared threatened, but instead found far north of their natural habitat. I personally also encountered a site with a clathrate blowout in the sub arctic, smaller than others shown in the news but still worrying.
And also got images taken of so much plastic in the ocean that I honestly have no idea how to deal with the amount of refuse that now find it’s way into the digestive system of animals of all sizes.
Not to mention the problems caused by the food industry.
https://bit.ly/3kUKAw6
The time is long past to do the osprey maneuver by putting the head in the ground denying the problem, if we’re to see this grand future in space – it’s not the environmentalists who need to be drafted for Zubrin, but the space advocates that rather need to become environmentalists!
Andrei: like
It is the difference between logistics and strategy/tactics in the military.
Every concept for the exploration and exploitation of space has to be bounded or constrained by hard science, or it would be dismissed outright. Likewise most of the doomsayer literature has a valid basis in science. It even has a niche in the space narrative in the filters associated with Fermi’s paradox.
The Scylla & Charybdis of resource depletion and environmental disruption are upon us, and whether we can negotiate these Great Filters and thrive on the other side will be a matter of conjecture until the outcome is manifest. Likewise Dyson spheres, Matrioshka brains, Shkadov thrusters and Kardashev III civilizations will all remain a matter of conjecture unless they are manifest.
Scientific validity does not equate to pragmatic possibility. But ruminating over this does not help.
Let’s keep in mind, too, that the topic of the post is Dr. Zubrin’s idea for a space telescope of extraordinary size, not his views on climate change. Let’s nudge back in that direction.
I do not wish to sidetrack any aspect of this interesting conversation on mega-scale space telescopes. Even if only partially realized, such technology could lead to unimaginable discoveries. Frankly, the technical aspects are in areas that I can not contribute.
However, I will comment on the increasing frequency of using thought-stopping labels of “psuedo science” and “fake news”. You may disagree with Zubrin in some areas but it is not your job nor a job for anyone else to determine what is to be considered and what is not to be considered in public discourse. In a different context, Shakespeare said it best “The lady doth protest too much, methinks”
In your recent page..
https://centauri-dreams.org/
A Method for Creating Enormous Space Telescopes
This line:-
“The reflector, however, hanging 1 km below the CubeSat will only be moving at 7667.50 km/s, generating a centrifugal acceleration of 8.675 m/s2. ”
The units should be m/s not km/s. It implies that the cubesat moves at 7.6 million m/s, or about 2.5% of the speed of light, so the new speed seems a bit high to me. The line above is correct. At an altitude of 400 km, the CubeSat will be moving with a velocity of 7668.63 m/s.
Then:
“The Earth’s gravitational acceleration at that altitude will be 8.679 m/s.” The units should be m/s^2
I’m not sure but maybe you could use the word ‘put’ instead of ‘plus’ in the line below?
“If we plus 120,000 kg into equation (1),”
The topic is very interesting, I see you covered solar gravitational lensing already. Many good comments there too. My personal feeling is that a surface error analysis and active correction is going to be key.
Radio telescopes are the obvious first application because accuracy doesn’t need to be high.
There is a good discussion of free flying elements in the comments, but what is really needed is a way to make small but sufficiently accurate elements (eg setting a surface liquid) then a way to string them together with adjustable wires and keep them in the right place.
The structure could still be low mass. If adjustable threads aren’t employed then it might be that electromagnetic standing wave resonance from the center of curvature could be used. The small force would be adequate in space and slightly different resonance frequencies could be used radially.
This is the effect where two parabolic dishes on an air track with a microwave resonance will always maintain their separation, if one moves then so does the other. I suspect that it works for dish alignment but haven’t seen this done.
Is there any need for radiotelescopes of this size in freefall? We had Arecibo at 305m and the new Chines FAST is 500m. They operate in wavelengths where there is effectively no atmospheric absorption. The only issue that I am aware of is structure mass. Then we have the distributed radio telescopes like LOFAR that can integrate the signals from each sensor.
I think the best application is as solar concentrators. I have already suggested use for solar thermal engines. Another application could be for vaporizing materials for asteroid deflection rather than far more expensive lasers (e.g. Lubin’s D-STARs). On fixed surfaces, concentrators can be lots of flat mirrors. In Ian McDonald’s Luna novels, such mirror arrays on sun-following tracks smelt the lunar regolith for metals. Conceivably, many flat, foil mirrors on lightweight carbon fiber or aluminum truss could be deployed instead of a single curved mirror as a concentrator in space. J P Aerospace have been building such lightweight truss structures for their proposed extreme altitude Dark Sky Station. There has also been ideas to use robots to build huge structures like webs as telescope supports and hulls of space habitats.
This discussion won’t be complete without at least acknowledging the possibility of using meta lenses in telescopes. It’s a fairly new technology and most discussion right now revolves around uses such as camera lenses and virtual reality displays but the promise is there for possible use in lightweight telescopes. The question of scalability remains and I can find nothing regarding the feasibility of using them in space based telescopes but I suspect radiation might be a very difficult hurdle. One issue has been resolved recently and that is the ability to focus the lenses. The technology holds out the promise of obsoleting current telescopes.
Sorry to chime in so late in the discussion. One of the biggest issues with a very large and very flexible mirror is the mechanical stability problem in repointing the telescope. It would be nice to be able to point the telescope at different objects, right?
To simplify the mechanical structure, Zubrin’s illustration of the electrostatic example shows the mirror supported only at the periphery. So imagine the entire telescope structure rotating a few degrees. How long does it take the flexible mirror to reach the correct new shape to within 100 nanometers (quarter wavelength)?
Without any damping, it would take a very long time. It might be possible to add damping with a grid of electrostatic actuators, but that means being able to quickly measure the mirror curvature to form the canceling forces across the mirror. That’s a pretty big complication to me.
What happened to MOIRE telescope design? I remember it being publicized as a breakthrough telescope using membrane, and it seems very similar to idea described in this article. It went very quiet later.
https://www.ball.com/aerospace/programs/moire
This idea is very interesting, but without resolution vs. surface error analyze further discussions are not serious.
I am sure there is a theoretical limit which dictates – that mirror with diameter bigger that some value will not give any improvements in telescope resolution for every specific wavelength.
I suppose that more serious scientific analysis of EST can discover that 1km EST will not have any advantage over 6m EST…