Centauri Dreams
Imagining and Planning Interstellar Exploration
HD 219134: Fine-Tuning Stellar Music
HD 219134, an orange K-class star in Cassiopeia, is relatively close to the Sun (21 light years) and already known to have at least five planets, two of them being rocky super-Earths that can be tracked transiting their host. We know how significant the transit method has become thanks to the planet harvests of, for example, the Kepler mission and TESS, the Transiting Exoplanet Survey Satellite. It’s interesting to realize now that an entirely different kind of measurement based on stellar vibrations can also yield useful planet information.
The work I’m looking at this morning comes out of the Keck Observatory on Mauna Kea (Hawaii), where the Keck Planet Finder (KFP) is being used to track HD 219134’s oscillations. The field of asteroseismology is a window into the interior of a star, allowing scientists to hear the frequencies at which individual stars resonate. That makes it possible to refine our readings on the mass of the star, and just as significantly, to determine its age with higher accuracy.
KPF uses radial velocity measurements to do its work, a technique often discussed in these pages to identify exoplanet candidates. But in this case measuring the motion of the stellar surface to and from the Earth is a way of collecting the star’s vibrations, which are the key to stellar structure. Says lead author Yaguang Li (University of Hawaii at Mānoa):
“The vibrations of a star are like its unique song. By listening to those oscillations, we can precisely determine how massive a star is, how large it is, and how old it is. KPF’s fast readout mode makes it perfectly suited for detecting oscillations in cool stars, and it is the only spectrograph on Mauna Kea currently capable of making this type of discovery.”

Image: Artist’s concept of the HD219134 system. Sound waves propagating through the stellar interior were used to measure its age and size, and characterize the planets orbiting the star. Credit: openAI, based on original artwork from Gabriel Perez Diaz/Instituto de Astrofísica de Canarias. The 10-second audio clip transforms the oscillations of HD219134 measured using the Keck Planet Finder into audible sound. The star pulses roughly every four minutes. When sped up by a factor of ~250,000, its internal vibrations shift into the range of human hearing. By “listening” to starlight in this way, astronomers can explore the hidden structure and dynamics beneath the star’s surface.
What we learn here is that HD 219134 is more than twice the age of the Sun at about 10.2 billion years old. The age of a star can be difficult to determine. The most widely used measurement involves gyrochronology, which focuses on how swiftly a star spins, the assumption being that younger stars rotate more rapidly than older ones, with the gradual loss of angular momentum traceable over time. The problem: Older stars don’t necessarily follow this script, with their spin-down evidently stalling at older ages. Asteroseismology allows a more accurate reading for stars like this and provides a different reference point, providing that our models of stellar evolution allow us to interpret the results correctly..
We need to track this work because how old a star is has implications across the board. For one thing, understanding basic factors such as its temperature and luminosity requires a context to determine whether we’re dealing with a young, evolving system or a star nearing the transition to a red giant. From an astrobiological point of view, we’d like to know how old any planets in the system are, and whether they’ve had sufficient time to develop life. SETI also takes on a new dimension when considering stellar age, as targeting older exoplanet systems allows us to put our focus on higher priority targets.
Yaguang Li thinks the KPF work brings new levels of precision to these measurements, calling the result ‘a long-lost tuning fork for stellar clocks.’ From the exoplanet standpoint, stellar age is also quite informative. For the measurements have allowed the researchers to determine that HD 219134 is smaller than previously thought by about 4% in radius – this contrasts with interferometry measurements that measured its size via multiple telescopes. A more accurate reading on the size of the star affects all inferences about its planets.
That 4% difference, though, raises questions, and the authors note that it requires the models of stellar evolution they are using to be accurate. From the paper:
We were unable to easily attribute this discrepancy to any systematic uncertainties related to interferometry, variations in the canonical choices of atmospheric boundary conditions or mixing-length theory used in stellar modeling, magnetic fields, or tidal heating. Without any insight into the cause of this discrepancy, our subsequently derived quantities and treatment of rotational evolution—all of which are contingent on these model ages and radii—must necessarily be regarded as being only conditional, pending a better understanding of the physical origin for this discrepancy. Future direct constraints on stellar radii from asteroseismology (e.g., through potential breakthroughs in understanding and mitigating the surface term) may alleviate this dependence on evolutionary modeling.
So we have to be cautious in our conclusions here. If indeed the tension between the KPF measurements and interferometry is correct, we will have adjusted our calibration tools for transiting exoplanets but still need to probe the reasons for the discrepancy. That’s important, because with tuned-up measurements of a star’s size, the radii and densities of transiting planets can be more accurately measured. The updated values KPF has given us – assembled through over 2000 velocity measurements of the star – point to a significant aspect of stellar modeling that may need further adjustment.
The paper is Yaguang Li et al., “K Dwarf Radius Inflation and a 10 Gyr Spin-down Clock Unveiled through Asteroseismology of HD 219134 from the Keck Planet Finder,” Astrophysical Journal Vol. 984, No. 2 (6 May 2025), 125 (full text).

Writing a Social Insect Civilization
Communicating with extraterrestrials isn’t going to be easy, as we’ve learned in science fiction, all the way from John Campbell’s Who Goes There? To Ted Chiang’s Story of Your Life (and the movie Arrival). Indeed, just imagining the kinds of civilizations that might emerge from life utterly unlike what we have on Earth calls for a rare combination of insight and speculative drive. Michael Chorost has been thinking about the problem for over a decade now, and it’s good to see him back in these pages to follow up on a post he wrote in 2015. As I’ve always been interested in how science fiction writers do their worldbuilding, I’m delighted to publish his take on his own experience at the craft. Michael is also the author of the splendid World Wide Mind: The Coming Integration of Humanity, Machines, and the Internet (Free Press, 2011) and Rebuilt: My Journey Back to the Hearing World (Mariner, 2006).
by Michael Chorost

Ten years ago, Paul Gilster kindly invited me to guest-publish an entry on Centauri Dreams titled, “Can Social Insects Have a Civilization?” At the time I was planning to write a nonfiction book about the linguistic issues of communicating with extraterrestrials. Though actual, face-to-face contact anytime soon is deeply unlikely, the concept is nonetheless theoretically interesting because it casts light on buried assumptions about language and communication. I sold the concept to Yale University Press. The working title was HOW TO TALK TO ALIENS.
I got busy, but I soon began to feel that the project was rather empty. I realized that in an actual First Contact situation, we’ll suddenly find ourselves in a complicated situation with a deeply unfamiliar interlocutor that has an agenda of its own. We’ll inevitably find ourselves winging it. Theory could be irrelevant. Useless.
For a while I tried to finesse the problem by putting scenarios in between the theoretical stuff. I imagined a human and an alien talking—specific humans, specific aliens, concrete settings. I soon realized that the scenarios were the most interesting material in the book.
That’s because positing a concrete situation made the problems, and the possible solutions, stand out clearly. Given a particular situation, what would people actually do?
It dawned on me: It made more sense to write the book as a novel. I withdrew from my contract at Yale and returned the advance. They were kind and understanding about it.
So I committed myself to a novel—but I wanted it to be as content-rich as the book I’d promised to Yale. I decided that the human characters would be scientists: an entomologist, a linguist, a neuroscientist, and a physicist. To succeed they’d have to pool their expertise, educating each other. That would imbue the novel with the scientific content.
But this risked me writing a deadly dull novel larded with exposition. I wanted the characters—both human and alien—to be vivid and unforgettable, and for their actions to drive a propulsive plot. I wanted the reader to be unable to put the book down.
I think I succeeded. I hired an editor to help me, and she made me do rewrites for three years; she was relentless. But at last she said, “You set yourself one of the hardest imaginative problems you could possibly have chosen, especially for a first novel. I think you managed it in a way that feels genuinely convincing. I want to say clearly upfront: this book is worth it. There is no story like this in the world.”
So I’m pretty confident that I now have a publishable novel—but getting there was really hard. I thought it would take about three years to write, which is how long my two nonfiction books took. I was wrong. It took eight.
When I started, I knew I wanted the aliens to be really alien: no pointy-eared, English-speaking Vulcans. I decided to make them sapient social insect colonies. That would make them aliens without contiguous bodies. Without hands as we know them. Without faces.
Therefore, I first had to figure out what a social insect civilization looks like. I didn’t want to take the easy way out by positing (as Orson Scott Card did) that a social insect colony would have a centralized intelligence, e.g. a Queen that gives orders. I felt that was cheating. I wanted the colonies to be genuinely distributed entities in which no individual insect has language or even much in the way of consciousness. Furthermore, I wanted the insects to be no bigger than Earthly ones, which ruled out big brains of any kind.
This gave me some very challenging questions. (From now on I’ll use the word “hive” as shorthand for “social insect colony.”)
• How does a hive pick up a hammer?
• How does a hive store and process the information needed for language?
• What is the physical structure of the hives?
• How does a distributed consciousness behave?
• What does such a civilization’s technology look like?
• What does its language look like? What’s its morphology, grammar, vocabulary?
• What does a society of hives look like?
• What events in the past set this species on the path to language and technology?
It took me two years just to answer the first one about picking up a hammer. I would imagine a bunch of insects clustering around a hammer and completely failing to get any leverage. Then I’d give up, deciding the question was unanswerable.
But finally, I figured it out: the hives parasitize mammals by inserting axons into the motor cortexes of their brains. That way, they can control the mammals as roaming “hands.”
And this was a key insight, because it helped me understand the hives as truly distributed entities. A given hive could have several dozen “hands” roaming the landscape, doing various things. Furthermore, it would have no front or back in any human sense.
This worldbuilding was fun, but it was the least efficient way imaginable to write a novel. I designed the aliens and their world before working out the plot. This led to a big problem.
Which was this: the aliens were so alien that I didn’t know why they would want to interact with humans in any way, nor us with them. What would we want to talk about? Or do together? This meant I didn’t have a plot.
I didn’t want to default to science fiction’s classic reasons for interspecies communication: war and trade. They struck me as stereotypical answers that would lead to a stereotypical novel. Besides, they begged the question. Species that are trading or fighting have to be similar enough to have things to trade, or to fight about. That would vitiate my goal of writing really alien aliens.
So I knew what kind of plots I didn’t want. But that didn’t tell me what kind of plot I did want. I sat down every day and wrote, hoping to figure out an answer.
This was, as I said, a very inefficient way to write a novel. Why didn’t I practice by writing, and publishing, a few short stories? Build up my cred, get my name out there? But I didn’t want to do those things. I wanted to write this novel. I grimly stuck to it, day after day.
After a while I had a bare-bones plot. When Jonah Loeb, a deaf graduate student in entomology, asks how to deal with an intelligent ant colony besieging Washington, D.C., the answer is, “Ask it to stop.” Jonah gathers a team of scientists and travels to a hive civilization in order to learn how.
I gave the other scientists names, figured out their dissertation topics, and worked out some of their characteristics. The neuroscientist was arrogant. The linguist was prickly and defensive. The physicist was socially awkward. Jonah, the protagonist, was deaf, like me, with cochlear implants. He was smart, but neurotic.
But I didn’t know how to make the characters come alive on the page. They all talked the same. Their only motivation was scientific interest. They had scant backstories or inner lives. They were, in short, boring.
I was even more at sea with the alien characters. They had no personality. I mean, really, how do you give a social insect colony a personality?
The plot, too, remained threadbare. I fabricated encounters, goings to-and-fro, arguments. But it just didn’t hold together. Often I’d add a new element only to realize it invalidated another element.
So I had dull characters and a plot made out of cardboard and duct tape. Finally, I admitted I needed help. I hired a freelance editor, and we started fresh.
The editor had me write up descriptions of each character’s goals and motives, and a detailed plot outline. We went through the manuscript one scene at a time, and she often told me to rework it before we went on to the next.
Slowly, the characters came to life on the page. I had made the protagonist, Jonah, deaf because I thought that would underscore the theme of communication. But Jonah only came to life when I thought back to my own feelings in my early twenties. I realized that Jonah was driven by feeling like an outsider. He desperately wants to be included and to prove himself.
This characterization let me set up a key dynamic: an outsider protagonist trying to communicate with aliens—the ultimate outsiders. Clarity for the character led to clarity for the story.
I slowly got better at solving problems by framing them in terms of character and plot. I knew that Tokic, the hives’ language, would have to be exotic—but creating it overwhelmed me. I’m no grammarian, and certainly no inventor of languages.
But then I realized I only had to develop enough of the language to support the plot. I wanted the plot to turn on misunderstandings and mistranslations as the humans struggled to learn the language.
A key source of confusion, I realized, would come from how differently shaped the hives and humans are. Humans have arms and legs that are attached to them. On the other hand, a hive is essentially a giant, stationary head with dozens of “hands” roaming the landscape. Not only that, the “hands,” as parasitized mammals, have minds of their own. Hives give their hands general orders, and the hands work out the details. A hive can disagree with its parts, and its parts can disagree right back.
I realized that the part/whole distinction would be built deeply into Tokic, rather like how human languages build gender deeply into their grammar. (In English, consider how hard it is to talk about a person if you don’t know their gender.) When you’re addressing another entity in Tokic, you have to be very precise, on the level of grammar, about its partness or wholeness.
Now consider: To a hive, is a human being a whole or a part?
A hive would find this question really hard to answer. As a mammal, a human being looks like a “hand”—a part—but it talks like a whole. Yet in Jonah’s team, each member is legitimately a part. In Latin, membrum means “limb” or “part of the body.”
Jonah, as a cochlear implant user, is even trickier for a hive to understand. A cochlear implant is a computer; it runs on code and constantly makes decisions about what’s important for the user to hear. It’s a body part that literally thinks for itself. As such, Jonah is kind of hive-like. When a hive asks what Jonah is and the team gives it an answer it doesn’t understand, the hive attacks the team and they must run for their lives.
I worked out Tokic’s parts/wholes grammar, and that made it possible for me to write the scenes where things went wrong. These were tough scenes to write, because I had to keep track of what a hive said, what the humans thought it said, the humans’ mistaken reply, and so on. I also had to be careful not to let the scenes get bogged down.
I’ve noted how inefficient my writing process was. But I do think it was productive in one way: I spent so much time thinking about the novel that a great deal of information accreted in my mind. I think that led to more richness in the worldbuilding and the story than would have happened if I’d written it faster.
There’s so much more I haven’t mentioned, like how an alien robot reads Wallace Stevens’s poetry and names itself after him; the brutal 1.8-gee gravity of Formicaris and the unexpected solution that lets the human team function there; the superheavy stable element that facilitates interstellar travel; the electromagnetic weapon that gives humans Capgras syndrome; the octopoidal surgeon who operates on Jonah and Daphne to upgrade their cyborg parts; and the illustrations. I had those done by professional science illustrators.
So now you have a sense of what my novel’s about. It’s still titled HOW TO TALK TO ALIENS; I think its unconventionality, and slightly academic air, will help it stand out. I hope you’re now as excited about it as I am. You can see a bit more about it at my website, michaelchorost.com.
If you know of any literary agents who’d be interested—please let me know.

Is Planet Nine Alone in the Outer System?
It was Robert Browning who said “Ah, but a man’s reach should exceed his grasp, or what’s a heaven for?” A rousing thought, but we don’t always know where we should reach. In terms of space exploration, a distant but feasible target is the solar gravitational lens distance beginning around 550 AU. So far the SGL definitely exceeds our grasp, but solid work in mission design by Slava Turyshev and team is ongoing at the Jet Propulsion Laboratory.
Targets need to tantalize, and maybe a target that we hadn’t previously considered is now emerging. Planet Nine, the hypothesized world that may lurk somewhere in our Solar System’s outer reaches, would be such an extraordinary discovery that it would tempt future mission designers in the same way.
This is interesting because right now our deep space targets need to be well defined. I love the idea of Interstellar Probe, the craft designed at JHU/APL, but it’s hard to excite the public with the idea of looking back at the heliosphere from the outside (although the science return would be fabulous). Pluto was hard enough to sell to the powers that be, but Allen Stern and team got the job done because they had a whole world that had never been seen up close. Will Planet Nine, if found, turn out to be the destination that some budget-strapped team finds a way to explore?
We have a lot to learn about planetary demographics given that our planet-finding technologies work best for larger worlds closer in to their stars. But a recent microlensing study suggests that as many as one out of every three stars in our galaxy should host a super-Earth in a Jupiter-like orbit (citation below). Microlensing is helpful because it can reveal planets at large distances from their parent stars. Super-Earths appear to be abundant. If it exists, Planet Nine isn’t in a Jovian orbit, but it’s probably smaller than Neptune.
In so many ways this planet makes sense. We’ve found planets like it in innumerable stellar systems. We also know that mechanisms of gravitational slingshotting can push a planet either out of its system entirely or into an entirely new orbit, explaining our prior lack of detection. We’re talking about a planet on the order of a super-Earth or a mini-Neptune, the former larger than our planet but still rocky, the latter smaller than Neptune but gaseous.

Image: An illustration shows what Planet Nine might look like orbiting far from our Sun. We have found many such worlds around other stars, but finding one in our own backyard is taking time because of its distance and an orbit that is probably well off the ecliptic. Assuming a planet is there at all. Image credit: NASA/Caltech.
The evidence in the orbits of a number of outer system objects points to something perturbing their paths, and seems to implicate something big. Now we have, after years of evidence gathering and debate, at least a possible candidate for this world. In process at Publications of the Astronomical Society of Australia (PASA), although not yet published, the paper digs deep into data from the Infrared Astronomical Satellite as well as AKARI, a Japanese satellite somewhat more sensitive than IRAS and launched in 2006.
The distant Sedna and other similar bodies with unusual orbital characteristics tell us that something has to account for their high eccentricity and inclination, while a number of Kuiper Belt objects seem to be similarly affected, as shown in the orientation of their orbits (described through what is known as the argument of perihelion). Computations thus far indicate mass on the order of something equal to or greater than 10 Earth masses, with a semi-major axis of about 700 AU.
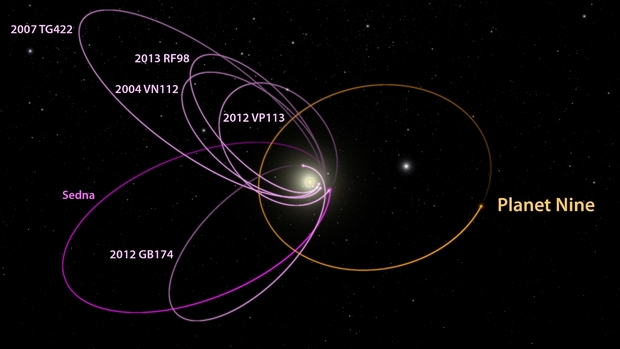
Image: The six most distant known objects in the solar system with orbits exclusively beyond Neptune (magenta) all mysteriously line up in a single direction. Moreover, when viewed in 3-D, the orbits of all these icy little objects are tilted in the same direction, away from the plane of the solar system. PL-Caltech/R. Hurt.
A huge amount of work has gone into this analysis, all ably summarized in the paper, which comes from Terry Long Phan (National Tsing Hua University, Taiwan) and colleagues. Optical surveys have heretofore failed to find this object, but 700 AU is fully 23 times the distance of Neptune from the Sun, far enough out that visible wavelengths need to give way to infrared to find it.
Phan’s team looked for candidate objects in the range of 500 to 700 AU using the two far-infrared surveys mentioned above, which are both all-sky in range but separated by 23 years, making for useful comparisons. The idea was to find an object that moved from an IRAS position to an AKARI position after those 23 years. Assuming the kind of mass and distance they were looking for, they had to remove stars and noisy sources toward galactic center. Narrowing the field to 13 pairings, Phan and his doctoral advisor Tomotsugu Goto found only one that matched in color and brightness, indicating they were the same object.
The paper cites the result this way:
After the rigorous selection including the visual image inspection, we found one good candidate pair, in which the IRAS source was not detected at the same position in the AKARI image and vice versa, with the expected angular separation of 42′ – 69.6′.
The AKARI detection probability map indicated that the AKARI source of our candidate pair satisfied the requirements for a slow-moving object with two detections on one date and no detection on the date of 6 months before.

Image: This is Figure 5 from the paper. Caption: Comparison between IRAS (left) and AKARI (right) cutout images of our good candidate pair. The green circle indicates the location of IRAS source, while the white circle indicates the location of AKARI source. The size of each circle is 25′′. The yellow arrow with a number in arcminute shows the angular separation between IRAS and AKARI sources. The colour bar represents the pixel intensity in each image in the unit of MJy/sr. The AKARI source in the right panel is not visible as a real physical source due to the characteristics of AKARI-MUSL, which include moving sources without monthly confirmation. Credit: Phan et al.
This could be considered tantalizing but little more, because it is impossible from these two observations to determine an orbit for this object. The authors say that the 570 megapixel Dark Energy Camera (DECam) may be useful for follow-up observations. But I also noted an article in Science by Hannah Richter. The author quotes Caltech astronomer Mike Brown, who came up with the original Planet Nine hypothesis in 2016.
Brown argues that this object is not likely to be Planet Nine because its orbit would be far more tilted than what is predicted for the undiscovered world. In other words, a planet in this position would not have the observed effects on the Solar System. In fact, a planet in this orbit would make the calculated Planet Nine orbit itself unstable, which would eliminate Planet Nine altogether.
Is there an entirely different planet out there? Future observations will have to sort this out. It surprises me that it has taken so long for this kind of search to occur. Discoveries are made when seasoned observers can prompt up-and-coming scientists to consider avenues hitherto unexplored. I think we can applaud Phan’s doctoral adviser, Tomotsugu Goto, for the insight to suggest this direction of study for a young astronomer who will bear watching.
For now, returning to the thoughts with which I began this post, there are a few implications even for missions in their current planning stages. From the paper:
Several recent studies proposed and evaluated the prospects of future planetary and deep-space missions for the Planet Nine search, including a dedicated mission to measure modifications of gravity out to 100 AU (Buscaino et al. 2015), the Uranus Orbiter and Probe mission (Bucko, Soyuer, and Zwick 2023), and the Elliptical Uranian Relativity Orbiter mission (Iorio, Girija, and Durante 2023).
We’ll be going deeper into these missions in the future. For now, I find the interest in Planet Nine heartening, because even in budget-barren times, we can be doing useful science by way of exploration with existing instruments and considering designs for missions we will one day be able to send. On that score, Planet Nine – or perhaps even a different world equally distant from the Sun – is an incentive for propulsion science and a driver for the imagination.
The paper is Phan et al., “A Search for Planet Nine with IRAS and AKARI Data,” accepted for publication in Publications of the Astronomical Society of Australia (PASA). Preprint. The paper on super-Earths is Weicheng Zang et al., “Microlensing events indicate that super-Earth exoplanets are common in Jupiter-like orbits,” Science Vol 388, Issue 6745 (24 April 2025), 400-404 (abstract).

New Horizons: Still More from System’s Edge
Even as I’ve been writing about the need to map out regions just outside the Solar System, I’ve learned of a new study that finds (admittedly scant) evidence for a Planet 9 candidate. I won’t get into that one today but save it for the next post, as we need to dispose of the New Horizons news first. But it’s exciting that a region extending from the Kuiper Belt to the inner Oort is increasingly under investigation, and the very ‘walls’ of the plasma bubble within which our system resides are slowly becoming defined. And if we do find Planet 9 some time soon, imagine the focus that will bring to this region.
As to New Horizons, there are reasons for building spacecraft that last. The Voyagers may be nearing the end of their lives, but given that they were only thought to be operational for a scant five years, I’d say their 50-year credentials are proven. And because they had the ability to hang in there, they’ve become our first interstellar mission, still reporting data, indispensable. Now we can hope that New Horizons carries on that tradition, since so far it has proven equally robust and remains productive.
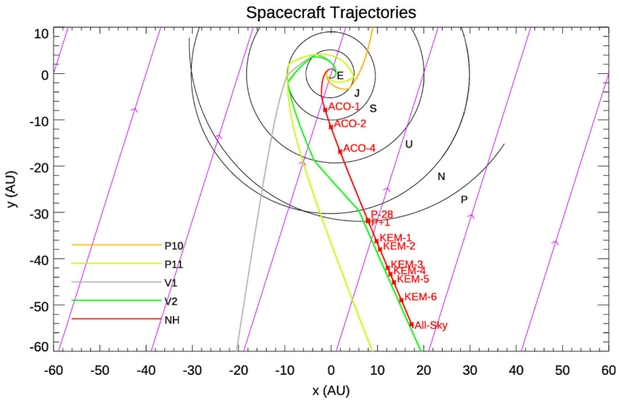
Image: This is Figure 1 from the paper we’ll be discussing today (citation below). Caption: The trajectories of the five spacecraft currently leaving the solar system: Pioneer 10 and 11 (orange and light green, respectively), Voyager 1 and 2 (gray and green, respectively), and New Horizons (NH, red) are shown projected onto the plane of the ecliptic, along with several planet orbits (black) and the direction of the flow of interstellar hydrogen atoms (purple arrows). The locations where great-circle scans of interplanetary medium (IPM) Lyα [a uniquely useful spectral line of hydrogen] were made with the NH Alice UV spectrograph are indicated (red), including the all-sky Lyα map described here, which was executed during 2023 September 2–11 at a distance from the Sun of 56.9 au. Credit: Gladstone et al.
To understand the image, we have to talk about ultraviolet Lyman-alpha (Lya) emissions, which happen when an electron in hydrogen transitions from the second energy level (n=2) down to the ground state (n=1). It is the transition that results in the production of a Lyman-alpha photon with a wavelength of about 121.6 nanometers. Since we’ve been talking about the interstellar medium lately, it’s helpful to know that photons in this far-ultraviolet part of the spectrum are absorbed and re-emitted by interstellar gas. They’re useful in the study of star-forming regions and molecular hydrogen clouds.
These emissions are at the heart of a new paper using data from New Horizons that has just appeared from the spacecraft’s team, under the guidance of Randy Gladstone, lead investigator and first author. Says Gladstone:
“Understanding the Lyman-alpha background helps shed light on nearby galactic structures and processes. This research suggests that hot interstellar gas bubbles like the one our solar system is embedded within may actually be regions of enhanced hydrogen gas emissions at a wavelength called Lyman alpha.”
So what we have in these Lyman-alpha emissions is a wavelength of ultraviolet light that is an outstanding tool for the study of the interstellar medium, not to mention our Solar System’s immediate surroundings within the Milky Way. The beauty of having New Horizons in the Kuiper Belt is that along the way to Pluto, the spacecraft was bankrolling Lya emissions with its ultraviolet spectrograph, charmingly dubbed Alice. Developed at SwRI, Alice was turned to the task of surveying Lya activity as the craft continued to travel ever farther from the Sun. One set of scans mapped 83% of the sky.
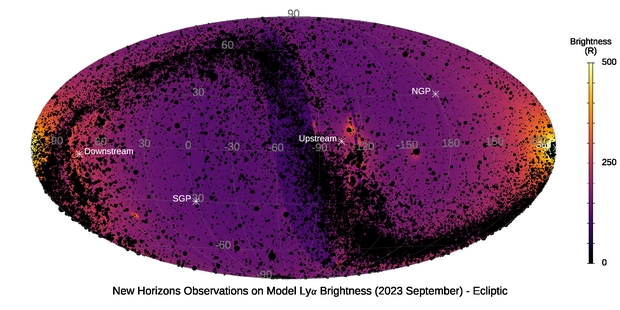
Image: The SwRI-led NASA New Horizons mission’s extensive observations of Lyman-alpha emissions have resulted in the first-ever map from the galaxy in Lyman-alpha light. This SwRI-developed Alice spectrograph map (in ecliptic coordinates, centered on the direction opposite the Sun) depicts the relatively uniform brightness of the Lyman-alpha background surrounding our heliosphere. The black dots represent approximately 90,000 known UV-bright stars in our galaxy. The north and south galactic poles are indicated (NGP & SGP, respectively), along with the flow direction of the interstellar medium through the solar system (both upstream and downstream). Credit: Courtesy of SwRI.
The method is about what you would assume: The New Horizons team could subtract the Lya activity from the Sun from the rest of the spectrographic data so as to get a read on the rest of the sky at the Lyman-alpha wavelength. What the team has found is a Lya sky about 10 times stronger than was expected from earlier estimates. And now we turn back to the issue of that hot bubble of gas – the Local Bubble – we talked about last time. 300 light years wide, the hot ionized plasma of the bubble was created by supernovae between 10 and 20 million years ago. The Sun resides within the Bubble along with low-density clouds of neutral hydrogen atoms, as we saw yesterday.
New Horizons has charted the emission of Lyman-alpha photons in the shell of the bubble, but the hydrogen ‘wall’ that has been theorized at the edge of the heliosphere, and the nearby cloud structures, show no correlation with the data. It is in the Local Interstellar Medium (LISM) background that the relatively bright and uniform signature of Lya is most apparent, evidently the result of hot, young stars within the Local Bubble shining on its interior walls. But as the authors note, this is currently just a conjecture. Further work from the doughty spacecraft may be in the cards. From the paper:
The NH Alice instrument has been used to obtain the first detailed all-sky map of Lyα emission observed from the outer solar system, where the Galactic and solar contributions to the observed brightness are comparable, and the solar contribution can be reasonably removed….A follow-up NH Alice all-sky Lyα map may be made in the future, if possible, and combining that map with this map could result in a considerable improvement in angular resolution. Finally, the maps presented here were obtained using the Alice spectrograph as a photometer, since its spectral resolution is too coarse to resolve the details of the Lyα line structure. However, there are instruments capable of resolving the Lyα line profile (e.g., J. T. Clarke et al. 1998; S. Hosseini & W. M. Harris 2020) which could possibly study this emission in more detail, and thus (even from Earth orbit) provide a new window on the LISM and H populations in the heliosphere.
Thus we learn something more about the boundary between our system and the interstellar medium in a map that should provide plenty of ground for new investigations at these wavelengths. And we’re reminded of the tenacity of well-built spacecraft and their continuing ability to return solid data well beyond their initial mission plan. Where and when the next interstellar craft gets built remains an open question, but for now New Horizons seems capable of a great deal more exploration.
The paper is Gladstone et al., “The Lyα Sky as Observed by New Horizons at 57 au,” The Astronomical Journal Vol. 169, No. 5 (25 April 2025), 275. Full text.

Charting the Interstellar Medium
We don’t talk about the interstellar medium as much as we ought to. After all, if a central goal of our spacefaring is to probe ever further into the cosmos, we’re going to need to understand a lot more about what we’re flying through. The heliosphere is being mapped and we’ve penetrated it with still functioning spacecraft, but out there in what we can call the local interstellar medium (LISM) and beyond, the nature of the journey changes. Get a spacecraft up to a few percent of the speed of light and we have to think about encounters with dust and gas that affect mission design.
Early thinking on this was of the sort employed by the British Interplanetary Society’s Project Daedalus team, working their way through the design of a massive two-staged craft that was intended to reach Barnard’s Star. Daedalus was designed to move at 12 percent of lightspeed, carrying a 32 meter beryllium shield for its cruise phase. Designer Alan Bond opined that the craft could also deploy a cloud of dust from the main vehicle to vaporize enroute particles before they could reach the shield.
Other concepts for dust mitigation have included using beamed energy to deflect larger objects, or in the case of micro-designs like Breakthrough Starshot, simply turning the craft to present as little surface area along the path of flight as possible, acknowledging that there is going to be an attrition rate in any swarm of outgoing probes. Send enough probes, in other words, and a workable percentage of them should get through.

Image: A dark cloud of cosmic dust snakes across this spectacular wide field image, illuminated by the brilliant light of new stars. This dense cloud is a star-forming region called Lupus 3, where dazzlingly hot stars are born from collapsing masses of gas and dust. This image was created from images taken using the VLT Survey Telescope and the MPG/ESO 2.2-metre telescope and is the most detailed image taken so far of this region. Credit: ESO/R. Colombari.
However we manage it, dust mitigation appears essential. Dana Andrews once calculated that for a starship moving at 0.3 c, a tenth of a micron grain of typical carbonaceous dust would have a relative kinetic energy of 37,500,000 GeV.. So understanding what’s around us, and in particular the gas and dust environment beyond but near the Solar System, is essential for future probes. For those wanting to brush up, the best overview on the interstellar medium remains Bruce Draine’s Physics of the Interstellar and Intergalactic Medium (Princeton, 2010).
Of course, most of the interstellar medium is made up of gas rather than dust, at a ratio of something like 99 to 1. The dust effect can be catastrophic, but the presence of this hydrogen and helium has been invoked by people like Robert Bussard because it could theoretically provide fuel to an interstellar ramscoop craft. Current thinking leans away from the idea, but it’s interesting to learn that we have sources of hydrogen far larger than we realized and also much closer to the Sun than, say, the Orion Nebula.

Thus my interest in a new paper out of Rutgers University. An international team working with astrophysicist Blakesley Burkhart has identified a hitherto unobserved cloud that could one day spawn new stars. Composed primarily of molecular hydrogen and dust, along with carbon monoxide, the cloud emerged in studies at far-ultraviolet wavelengths. The discovery is unusual because it is difficult to observe molecular hydrogen directly. Most observations of such clouds have to employ radio and infrared data, where the signature of CO is a clear tracer of the mass of molecular hydrogen.
Image: Blakesley Burkhart, a Rutgers University astrophysicist, has led a team that discovered the molecular hydrogen gas cloud, Eos. Credit: Rutgers University.
The data for this work were collected by FIMS-SPEAR (fluorescent imaging spectrograph), a far-ultraviolet instrument aboard the Korean satellite STSAT-1. Named Eos, the new cloud turns out to be one of the largest single structures in the sky. It is located some 300 light years away at the edge of the Local Bubble, and masses about 3400 times the mass of the Sun. The Solar System itself resides within the Local Bubble, which is several hundred parsecs in diameter and was probably formed by supernovae that created a hot interior cavity now surrounded by gas and dust. The nearby star-forming regions closest to the Sun are found along the surface of this bubble.
If we could see it with the naked eye, Eos would measure about forty moons across the sky. The likely reason it has not been detected before is that it is unusually deficient in carbon monoxide and thus hard to find with more conventional methods. Says Burkhart:
“This is the first-ever molecular cloud discovered by looking for far ultraviolet emission of molecular hydrogen directly. The data showed glowing hydrogen molecules detected via fluorescence in the far ultraviolet. This cloud is literally glowing in the dark.”
And getting back to dust, this work usefully shows us how we’re beginning to map relatively nearby space to locate concentrated areas of such matter. From the paper:
Using Dustribution [a 3D dust mapping algorithm], we compute a 3D dust map of the solar neighbourhood out to a distance of 350 pc. Figure 3 [below] shows the reconstructed map, focusing on the region of the Eos cloud as a function of distance. We see a single, distinct cloud that corresponds to the H2 emission stretching from 94 to 130 pc; no other clouds are visible along the same lines of sight in Fig. 3. This establishes the cloud as among the closest to our Solar System, on the near side of the Sco–Cen OB association [Scorpius–Centaurus Association, young stars including the Southern Cross formed from the same molecular cloud]…

Image: This is part of Figure 3 from the paper. Caption: 3D dust density structure of the Eos cloud. Two-dimensional slices of the cloud at different distances. The colour bar indicates both the total dust extinction density and the total mass density, assuming dust properties from ref. 29 and a gas-to-dust mass ratio of 124… [T]he magenta contour shows the region with high H2/FUV ratio. Credit: Burkhart et al.
And I quite like this video the scientists have put together illustrating the cloud and its relationship to the Solar System.
Image: Scientists have discovered a potentially star-forming cloud and called it “Eos.” It is one of the largest single structures in the sky and among the closest to the Sun and Earth ever to be detected. Credit: Thomas Müller (HdA/MPIA) and Thavisha Dharmawardena (NYU).
The paper is Burkhart et al., “A nearby dark molecular cloud in the Local Bubble revealed via H2 fluorescence,” Nature Astronomy 28 April 2025). Full text.

Magnetic Collapse: A Spur to Evolution?
The sublime, almost fearful nature of deep time sometimes awes me even more than the kind of distances we routinely discuss in these pages. Yes, the prospect of a 13.8 billion year old cosmos strung with stars and galaxies astonishes. But so too do the constant reminders of our place in the vast chronology of our planet. Simple rocks can bring me up short, as when I consider just how they were made, how long the process took, and what they imply about life.
Consider the shifts that have occurred in continents, which we can deduce from careful study at sites with varying histories. Move into northern Quebec, for example, and you can uncover rock that was found on the continent we now call Laurentia, considered a relatively stable region of the continental crust (the term for such a region is craton). Move to the Ukraine and you can investigate the geology of the continent called Baltica. Gondwana can be studied in Brazil, an obvious reminder of how much the surface has changed.
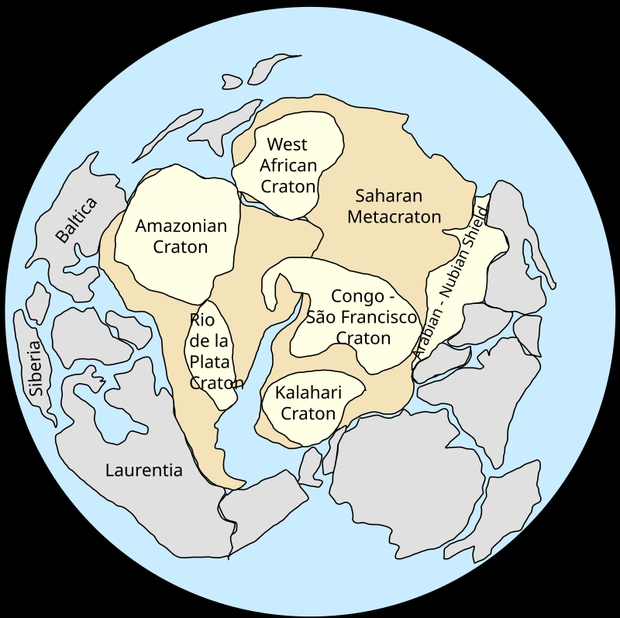
Image: With Earth’s surface constantly changing over time, we can only do snapshots to suggest some of these changes. Here is a view of the Pannotia supercontinent, showing components as they existed about 545 million years ago. Based on: Dalziel, I. W. (1997). “Neoproterozoic-Paleozoic geography and tectonics: Review, hypothesis, environmental speculation”. Geological Society of America Bulletin 109 (1): 16–42. DOI:<0016:ONPGAT>2.3.CO;2 10.1130/0016-7606(1997)109<0016:ONPGAT>2.3.CO;2. Fig. 12, p. 31. Credit: Wikimedia Commons.
Studying these matters has something of the effect of an earthquake on me. By which I mean that in the two minor earthquakes I have experienced, the sense of something taken for granted – the deep stability of the ground under my feet – suddenly became questionable. Anyone who has gone through such events knows that the initial human response is often mystification. What’s going on? And then suddenly the big picture emerges even as the quake passes.
So it can be with scientific realizations. Let’s talk about how scientists use various methods to study rock from different eras to infer changes to Earth’s magnetic field. Tiny crystal grains a mere 50 to a few hundreds of nanometers in size can hold a single magnetic domain, meaning a place where the magnetization exists in a uniform direction. Think of this as a locking in of magnetic field conditions that can be studied at various times in the planet’s history to see what the Earth’s magnetic field was doing then.

The subject is vast, and the work richly rewarding for anyone asking questions about how the planet has evolved. But now we’re learning that it also holds implications for the evolution of life. In a new feature in Physics Today, John Tarduno (University of Rochester) explains his team’s recent work on paleomagnetism, which is the study of the magnetic field throughout Earth’s history as captured in rock and sediment. For the magnetic poles move, and sometimes reverse, and within that history quite a story is emerging.
Image: The University of Rochester’s Tarduno, whose recent work explores the effects of a changing magnetic field on biological evolution. Credit: University of Rochester.
For Tarduno, the implications of some of these changes are striking. They grow out of the fact that the magnetic field, which is produced in our planet’s outer core (mostly liquid iron) continually varies, and the timescales involved can be short (mere years) or extensive (hundreds of millions of years). It’s been understood for a long time that the field reverses its polarity, but accompanying this change is the less known fact that a polarity change also decreases the field strength. Sometimes these transitions are short, but sometimes lengthy indeed.
Consider that new evidence, presented by Tarduno is this deeply researched backgrounder, shows that some 575 to 565 million years ago the Earth’s magnetic field all but collapsed, and remained collapsed for a period of tens of millions of years. If that time range piques your interest, it’s probably because this is coincident with a period known as the Avalon explosion, when macroscopic animal life, rich in complexity, begins to appear. And now we’re in the realm of evolution being spurred by magnetic field changes. The implications run to life’s own history and even as far out as SETI.

Named after the peninsula in which evidence for it was found, the Avalon explosion occurred tens of millions of years earlier than the Cambrian period which has heretofore been considered the time when complex lifeforms began to appear on Earth. It came during the Ediacaran period that preceded the Cambrian, and seems to have produced the first complex multicellular organisms. The sudden diversification of body scheme and distinct morphologies has been traced at sites in Canada as well as the UK.
Image: Archaeaspinus, a representative of phylum Proarticulata which also includes Dickinsonia, Karakhtia and numerous other organisms. They are members of the Ediacaran biota. Credit: Masahiro miyasaka / Wikimedia Commons.
So this is an ‘unexpected twist,’ as Tarduno puts it, that may relate significant evolutionary changes to the magnetic field as it reconfigured itself. Scientists studying the Ediacaran period (between 635 and 541 million years ago) have found that rocks formed then show odd magnetic directions. Some researchers concluded that the magnetic field in this period was reversing polarity, and we already knew that during a polarity reversal (the last was 800,000 years ago), the magnetic field could take on unusual shapes. Recent work shows that its strength in this period was a mere tenth of the values of today’s field.
This work was done in northern Quebec (ancient Laurentia), but later work from the Ukraine (Baltica) and Brazil showed an even lower field strength. We’re talking about a long period here of ultralow magnetic activity, perhaps 26 million years or more. Events deep inside the Earth’s inner core seem to have spurred this. I won’t go into the details about all the research on the core – it’s fascinating but would take us deeply into the weeds. For now, just consider that a consensus has been building that relates core activity to the odd Ediacaran geomagnetic field, one that correlates with a profound evolutionary event.
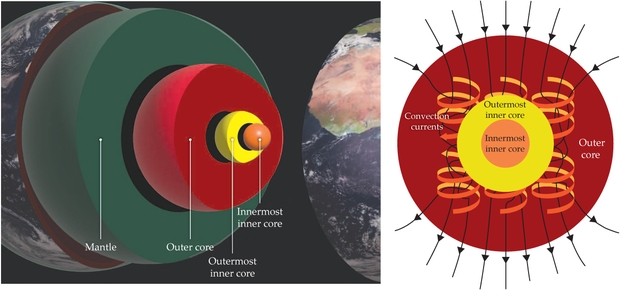
Image: This is Figure 2 from the paper. Caption: Changes deep inside Earth have affected the behavior of the geodynamo over time. In the fluid outer core, shown at right, convection currents (orange and yellow arrows and ribbons) form into rolls because of the Coriolis effect from the planet’s rotation and generate Earth’s magnetic field (black arrows). Structures in the mantle—for example, slabs of subducted oceanic crust, mantle plumes, and regions that are anomalously hot or dense—can affect the heat flow at the core–mantle boundary and, in turn, influence the efficiency of the geodynamo. As iron freezes onto the growing solid inner core, both latent heat of crystallization and composition buoyancy from release of light elements provide power to the geodynamo. (Left: Earth layers image adapted from Rory Cottrell, Earth surface image adapted from EUMETSAT/ESA; right: image adapted from Andrew Z. Colvin/CC BY-SA 4.0.)
In the models Tarduno describes, the Cambrian explosion itself was driven by a greater incidence of energetic solar particles during periods of weak magnetic field strength. Thus we have the basis for a weak field increasing mutation rates and stimulating evolutionary processes. Tarduno cites his own work here:
Eric Blackman, David Sibeck, and I have considered whether the linkage might be found in changes to the paleomagnetosphere. Records of the strength of the time-averaged field can be derived from paleomagnetism, whereas solar-wind pressure can be estimated using data from solar analogues of different ages. My research group and collaborators have traced the history of solar–terrestrial interactions in the past by calculating the magnetopause standoff distance, where the solar-wind pressure is balanced by the magnetic field pressure… We know that the ultralow geomagnetic fields 590 million years ago would have been associated with extraordinarily small standoff distances, some 4.2 Earth radii (today it is 10–11 Earth radii) and perhaps as low as 1.6 Earth radii during coronal mass ejection events.
As Tarduno explains, all this leads to increased oxygenation during a period of magnetic field strength diminished to an all-time low, along with an accompanying boom in the complexity of animal life from the Ediacaran leading into the Cambrian.
Notice the profound shift we are talking about here. Classically, scientists have assumed that it was the shielding effects of the magnetic field that offered life the chance to survive. Indeed, we talk about a lack of magnetic fields in exoplanets like Proxima Centauri b as being a strong danger to life because of incoming radiation. This new work is saying something profound:
If our hypothesis is correct, we will have flipped the classic idea that magnetic shielding of atmospheric loss was most important for life, at least during the Ediacaran Period: The prolonged interlude when the field almost vanished was a critical spark that accelerated evolution.
Maybe we have been too simplistic in our views of how a magnetic field influences the development and growth of lifeforms. In recent decades, work has been showing linkages between these magnetic changes, which can last for millions of years, and spurts in evolutionary activity. So that it is precisely because of low magnetic field strength, rather than in spite of it, that life suddenly explodes into new forms during these periods of high activity.
Jim Benford has often commented to me that despite having mounted the most intensive SETI search with the most powerful tools ever available, we still have not a trace of a signal from another civilization. Is it possible – and Jim was the one who pointed out this paper to me – that the reason is that the magnetic field changes that so affected life on our planet are rare elsewhere? Because it now looks as though a magnetic field should be considered less a binary situation than as a variable, one whose mutability because of core activity can take the world it engulfs into periods of low to high magnetic strength, and some eras millions of years long in which there is hardly any field at all.
I mentioned Proxima Centauri b above. Whether or not it has a magnetic field has yet to be determined, which points out how little we know about such fields around exoplanets at large. Further investigation of Earth’s magnetic past will help us understand how such fields change over time, and whether Earth’s own history has been unusually kind to evolution.
The article is Tarduno, “Earth’s magnetic dipole collapses, and life explodes,” Physics Today 78 (4) (2025), 26-33 (abstract).


