Exomoons continue to be elude us, though they’re under intense study. One detection strategy is called Orbital Sampling Effect, as explained in the article below. I’ll let Michael Hippke describe it, but the intriguing fact is that we can work with these methods using existing datasets to refine our techniques and actively hunt for candidates. Michael is a researcher based in Düsseldorf, Germany. With a background in econometrics, statistics and IT, he mastered data analysis at McKinsey & Company, a multinational management consulting firm. These days he puts his expertise to work in various areas of astrophysics, and most recently appeared here in our discussion of his paper on Fast Radio Bursts (see Fast Radio Bursts: SETI Implications?).
by Michael Hippke

Our own Solar System hosts 8 planets (plus Pluto and other “dwarf planets”), but 16 large moons with radii over 1,000km. And we have detected thousands of exoplanets – planets orbiting other stars – but not a single exomoon. The question of their existence is interesting, as some exomoons might in fact be habitable. Lately, there has been some speculation that, overall, there might be more habitable moons than planets in the universe. Consequently, we really want to know more about moons!
Moons are, by definition, smaller than their host planets, and thus harder to detect. Various search methods have been proposed – with the HEK project (Hunt for Exomoons with Kepler), led by David Kipping, being the most prominent team. A novel, promising method has been developed by René Heller in 2014, dubbed the “orbital sampling effect” (OSE). As with exoplanet transits, this method stacks many (dozens or ideally hundreds) of planet transits, and searches for the signature of a moon in this stack. While planet transit shapes are rather simple, the moon curves turn out the be very complex.
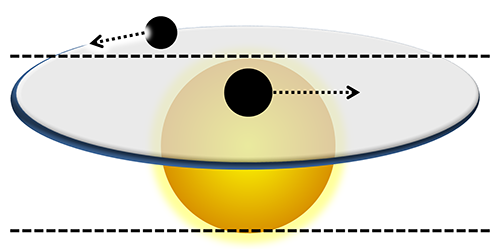
Image: A star with a transiting planet and its moon. The angled area shows the inclination of the moon orbit. Orbit positions beyond the dashed line are not undergoing transit, and are thus not observable.
In my recent work, I have processed data from the Kepler space telescope to search for this effect. I also worked with the “scatter peak,” an exomoon detection method described by Attila Simon (Konkoly Observatory, Hungary) and team in 2012. It is based on the fact that the geometrical exomoon configuration is very likely different during every exoplanet transit: On some transits, the moon might be ahead of the planet, on other transits behind it. When stacking many transits, at a given phase folded time, one gets a flux loss in some cases, and not in others. This results in increased scatter (photometric noise) when compared to out-of-transit times.
While the sole use of the scatter peak is problematic due to stellar noise, it can be used to confirm or reject certain signals. Not surprisingly, the struggle against stellar noise, instrumental jitter and other glitches has required the development of a complex statistical framework. While the Kepler data quality is at the very limit for exomoon hunting, a few very interesting results could be achieved.
The first result is sensitivity. What moons can we detect with Kepler and the OSE? Learning the answer to this will be useful for the assessment of future time-series photometry space missions, such as TESS or PLATO 2.0. With Kepler, the limit seems to be about 0.3 — 0.4 Earth radii for a moon to be detected, which is about the size of Ganymede. In many cases, where the host stars are dimmer, or noisier, only larger moons can be detected. Despite these limitations, my work shows that the OSE is a promising method, which will one day, with better data quality and/or processing, likely succeed and find moons!
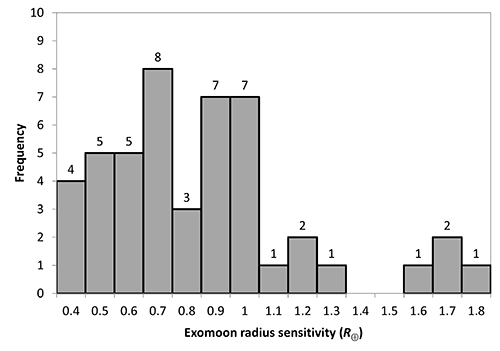
Image: The smallest radii detectable with the OSE in Kepler data are ~0.4 Earth radii. In many cases, the data and method only allows for the detection of larger moons. These are calculated limits, not real observations.
The second result is the ‘average moon’ effect. While no single moon could be detected, it is possible to “super-stack” a larger sample of planet-OSEs to estimate the average moon size in different samples. For very short-period planets with orbits shorter than about 15 days, no moons are seen. This is in agreement with stability arguments: The closer the planet to the star, the more the star “pulls” on the moon and tries to swallow it. The critical distance is not perfectly clear, but believed to be at ~15-day orbits. In my analysis, I find that the average moon signal comes up for periods over 35 days. In the sample of 35- to 80-day orbits, I find an average moon radius of about 2,000km (roughly like our moon). This estimate doesn’t tell how many planets actually have moons, or how many multiple moon systems are included in this average. It is for future studies (and telescopes) to determine this. But it is exciting that one can try.
The third result is about individual candidates. A small sample of planets shows prominent OSE-like signals justifying an in-depth analysis. It must be clearly said that, very likely, all of these will turn out to be false-positives. For some cases, it might even be possible to show that they cannot be moons, for example because some configurations are not stable over longer time frames. But this is not a bad result, for when we find false-positives, we can add the detection mechanism for these to our algorithm, and improve future searches.
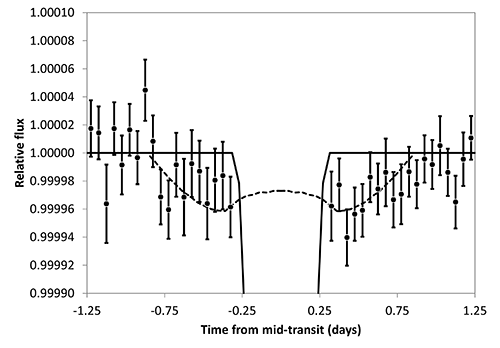
Image: Planet transit (straight line), moon effect due to the OSE (dashed line) and real datapoints (dots with error bars). In this case of Kepler-264b, the data are in favour of a moon interpretation, although this cannot be considered a detection, as detailed in the paper.
Personally, I would expect that the first moon(s) that will be found will be at the long (large/massive) end of exomoon distribution, as was the case for exoplanets. This comes from a selection bias: Large things are easier to see, and will thus be detected first. It will not mean that all moons are giants, as not all planets are Hot Jupiters (which were the first planets detected). Interesting times are ahead!
For more information, the paper is Hippke, “On the detection of Exomoons: A search in Kepler data for the orbital sampling effect and the scatter peak.” It has been accepted by the Astrophysical Journal for publication. A preprint is available.



Dear Michael. Thanks first for taking the time off to explain your exciting method to us and congratulations on a sophisticated piece of work fully acknowledged in its prestigious publication. I’ve read all of the HEK teams work and also Rene Hellers reflective pieces on what we might find. Given the delay as the technology catches up there has been time for considerable reflection into how to characterise a moon once it is inevitably found. Everyone is going to expect a habitable “Forest moon of Endor” of course.
Rene Hellers simulations suggestion “regular ” moons ( formed in situ from the same part of the protoplanetary disk as the parent planet ) can form up to 2 mass Mars or 0.2M Earth but that “irregular” moons ( captured KBOs or planets even ) of no clear definable upper limit are possible, most likely orbiting smaller Neptune sized planets given the lower closing velocities needed to avoid destruction or expulsion . If that is the case and as you point out , the bigger the more likely , the first exomoons could be irregular in nature . It’s hard enough to detect a moon but what can be told about its properties given currently available detection methods ? Astrometry is finally getting it’s act together and might make its first heavyweight appearance with a WFIRST/Gaia combination . Will that be able to help too or will it need more development? I know David Spergel hopes to use it to discover Earth mass planets around nearby stars .
Gaia / WFIRST is very much an opportunistic use of non dedicated technology hence its sensitivity extends over a only relatively short distance. I know that the two unit astrometric NEAT telescope concept and its recent descendent THEIA hoped to achieve the 0.5-1 microarc second resolution necessary to discover 0.5-1 Mass Earth planets out to 10 parsecs , in conjunction with the high precision RV spectrograph ESPRESSO /CODEX . I assume the increased sensitivity this bespoke technology brings would work perfectly with your model. Have you been able to simulate these various concepts ?
Hallo Ashley,
I have explored the limits of photometry in a recent paper (http://arxiv.org/abs/1503.03251), but for astrometry (GAIA,…) I am no expert. Do you know anyone who is? Would be cool to look into synergy effects.
Well, I do not consider myself an expert in astrometry but I am a physicist with some experience with orbital dynamics and can weigh in on this: I do not believe that astrometric measurements of a star made by Gaia or any other instrument can reveal the presence of a moon orbiting a planet which in turn is orbiting the star being observed. Astrometric measurements of a star reveals the reflex motion of an object with mass orbiting that star. How the mass is distributed in that “object” (whether it be a single body or a bound collection of many bodies including a planet with an orbiting moon) makes no difference on the magnitude of the star’s reflex motion. The magnitude of the reflex motion is dependent only on the mass of the star, the mass of the “object” and the distance between their centers of mass.
If we we are able to resolve the image of a planet, we could infer the the presence of an unseen moon by making precision astrometric measurements of the motion of the planet around the star. But it is not possible to infer the presence of a moon by observing the star itself like Gaia is doing.
@Andrew LePage
It’s not intuitive to me why the distribution of the “object” (in this case the planet and moon system) doesn’t affect the star’s reflex motion. My intuition is that it does matter, and that there would be some modulation of the star’s reflex motion as the planet and moon(s) orbit each other about their barycentre.
Concretely, if Mercury had a Pluto sized metallic moon, then wouldn’t the gravitational pull of the Mercury-and-moon system on the Sun be greatest when Mercury is directly between the barycentre and the sun, and least when when Mercury is on the far side of the barycentre?
Unless I misunderstood your comment, I think that you are saying the gravitational pull is invariant. This doesn’t quite make sense to me. Thanks
I’m very glad to be shown to be wrong, I hasten to add ;)
Just realised… above I wasn’t considering how the closest planet-star distance (when planet’s between the barycentre and the star) will be further than the closest moon-star distance (when the planet’s opposite the barycentre). Maybe I do now have an intuition for why the combined gravitational pull from the planet-moon system upon the star should be constant as they orbit about their barycentre – completely hand-wavey, of course
To first order the planet-moon system would behave as a single particle with the combined mass, but this is an approximation of the actual behaviour. There would be very small differences in the system’s motion, unfortunately this would be too small to detect for any realistic planet-moon system.
E.g. using the most sensitive method of the reflex motion-based planet detection methods, millisecond pulsar timing, it would be possible to detect a satellite orbiting PSR B1620-26 b providing it has a mass greater than ~5% of the parent planet, which works out as a satellite with somewhat more than twice the mass of Neptune.
@andy April 19, 2015 at 17:41
Many thanks for the reference!!! While my original assessment has been proven to be incorrect, it seems I was incorrect only by a very small amount. If my initial scan of the paper is correct, for example, the reflex motion of the Earth-Moon system around Sun would be modulated by the motion of the Moon revolving about the Earth by ~7.6X10^-16 of the reflex motion’s full amplitude with periods of ~15.4 and ~14.7 days. Considering that the amplitude of the reflex motion of the Sun about the barycenter of the Earth-Sun system amounts to something like ~450 kilometers, that makes the amplitude of the effect of the Moon orbiting the Earth amount to only 0.3 NANOmeters. While we could invent scenarios where that signal could be much larger, I strongly suspect that Gaia will be incapable of making measurements often enough and with sufficient accuracy to detect any moon orbiting an extrasolar planet. Still, I am looking forward to reading the paper in more detail and exploring “parameter space” to see if this detection method is might be practical under some circumstances using astrometry or precision radial velocity measurements.
What about using Astrometry to detect pairs of binary Brown Dwarf or super-Jupiter sized objects in orbit around larger stars?
If I remember correctly, commenters on here have said that super-Jupiters down to something like 8 Jupiter masses can form by themselves within molecular clouds. We’ve observed binary brown dwarfs already, indeed the third closest known system to the Sun is Luhman 16 which is a brown dwarf binary. If anyone has any information about the lower mass limits of binary objects, and the limits of their stability in orbit around a more massive star, it would be very interesting to hear.
Two questions, Michael (one ON topic, and one OFF) Question # ONE: Should the proposed sattilite of Kepler 264B BE confirmed, would astronimers regard this as an exomoon, or a component of a BINARY-PLANET system (which, if a recent paper on the subject is accurate, CAN FORM, but by a DIFFERENT mechanism than exomoon formation)? Question # TWO: There MAY be a way to PROVE that FRB110703 is NOT of EXTRAGALACTIC ORIGIN! The contact-binary star system, V233003-024818 is located at just about 10 arcminutes from the burst location. Shouldnt this mean (correct me if I am wrong) that the burst was GRVITATIONALLY LENSED if it was at a much furthur distance? Can a <4.3 ms signal even be ABLE to be analysed for a POTENTIAL microlensing event (or should I say "nanolensing"). If this is possible, and gravitational lensing WERE TO BE RULED OUT, then either the burst came from the stars themselves (as Avi Loeb et al, claim, OR, from even closer in, as you propose. PS: Should you CONFIRM that all the bursts SO FAR DID have arrival times aligned with UTC time, wouldn't it be extremely co-incidental that a relatively nearby star system would ALSO be ligned up this way as well? ALSO: If the five UNPUBLISHED FRB's DO NOT ALIGN with UTC time, shouldn't we consifer them as SEPARATE TYPES OF EVENTS (like FRB's and PERYTONS)?