The cascading numbers of exoplanet discoveries raise questions about how to interpret our data. In particular, what do we do about all those transit finds where we can work out a planet’s radius and need to determine its mass? Andrew LePage returns to Centauri Dreams with a look at a new attempt to derive the relationship between mass and radius. Getting this right will be useful as we analyze statistical data to understand how planets form and evolve. LePage is the author of an excellent blog on exoplanetary science called Drew ex Machina, and a senior project scientist at Visidyne, Inc. specializing in the processing and analysis of remote sensing data.
By Andrew LePage

As anyone with even a passing interest in planetary studies can tell you, we are witnessing an age of planetary discovery unrivaled in the long history of astronomy. Over the last two decades, thousands of extrasolar planets have been discovered using a variety of techniques. The most successful of these to date in terms of sheer number of finds is the transit method – the use of precision photometric measurements to spot the tiny decrease in a star’s brightness as an orbiting planet passes directly between us and the star. The change in the star’s brightness during the transit allows astronomers to estimate the size of the planet relative to the star while the time between successive transits allows the orbital period of the planet to be determined. Combined with information about the properties of the star being observed, other characteristics can be calculated such as the actual size of the planet and its orbit. The most successful campaign to date to search for planets using the transit method has been performed using NASA’s Kepler spacecraft, launched in 2009.
One of the other important bulk properties of a planet that is of interest to scientists is its mass. Unfortunately, the transit method is typically unable to supply us with this information except in special circumstances where planets in a system strongly interact with each other to produce measurable variations in the timing or duration of their transits. The transit timing variation (TTV) or transit duration variation (TDV) methods can be used to estimate the masses of the planets of a system including non-transiting planets that might be present. Based on an analysis of Kepler results to date, however, this method can be used in only about 6% of planetary systems that produce transits.
A more widely applicable method to determine the mass of an extrasolar planet is through the precision measurement of a star’s radial velocity to detect the reflex motion caused by the orbiting planet. Combined with information from transit observations as well as the star’s properties, it is possible to calculate the actual mass of a planet and further refine its orbital properties. Unfortunately, NASA’s Kepler mission has discovered thousands of planets and making precision radial velocity measurements takes a lot of time on a limited number of busy telescopes that are equipped to make the required observations. In addition, many of the stars observed by Kepler are too dim or their planets too small for the current generation of instruments to detect radial velocity variations above the noise. This is especially a problem for sub-Neptune size planets including Earth-size terrestrial planets. Taken as a whole, only a small minority of all of Kepler’s finds currently have had their masses measured.
Puzzling Out a Planetary Mass
While astronomers continue to struggle to measure the masses of thousands of individual extrasolar planets found by Kepler, there have been efforts to derive a mass-radius relationship so that the mass of a planet with a known radius can at least be estimated. In addition to being useful for evaluating the level of accuracy required for detection using radial velocity measurements or other methods, such mass estimates are also valuable for scientists wishing to use Kepler radius and orbit data in statistical studies of planetary properties, dynamics, formation and evolution. Over the past few years, there have been various investigators who have attempted to derive a planetary mass-radius relationship as information on the mass and radius of known planets has expanded. These relationships have taken a mathematical form known as a power law such as M = CRγ where M is the mass of the planet (in terms of Earth mass or ME), R is its radius (in terms of Earth radii or RE) and C and γ are constants determined by analysis.
The latest work to derive a mass-radius relationship for sub-Neptune size planets (i.e. planets whose radii are less than 4RE) is a paper by Angie Wolfgang (University of California – Santa Cruz), Leslie A. Rogers (California Institute of Technology), and Eric B. Ford (Pennsylvania State University), which they recently submitted for publication in The Astrophysical Journal. These sub-Neptune size worlds are of particular interest to the scientific community since they span the size range between the Earth and Neptune where no Solar System analogs exist to provide guidance for deriving a mass-radius relationship.
Earlier work over the last few years on the planetary mass-radius relationship relied on least squares regression analysis of a set of planetary radius and mass measurements – a fairly straightforward mathematical method used to determine the constants of an equation that provides the best fit to a set of data points. Unfortunately, this classic method has some drawbacks. It does not properly take into account the uncertainty in the independent variable (i.e. the planet radius, in this case) or instances where the planet has not been detected using precision radial velocity measurements and only an upper limit of the mass can be derived. Another issue is that the least squares regression method assumes a deterministic relationship where a particular planetary radius value corresponds to a unique mass value. In reality, planets with a given radius can have a range of different mass values, in part reflecting the variation in planetary composition running from massive rocky planets with large iron-nickel cores to less massive, volatile-rich planets with deep atmospheres. These variations are expected to be especially important in sub-Neptune-class worlds.
A Bayesian Approach to the Mass/Radius Problem
Instead of using the least squares regression method, Wolfgang, Rogers and Ford evaluated their data using a hierarchal Bayesian technique which allowed them not only to derive the parameters for a best fit of the available data, but also to quantify the uncertainty in those parameters as well as the distribution of actual planetary mass values. Using their approach, they have derived a probabilistic mass-radius relationship where the most likely mass and the distribution of those values are determined. The team considered a total of 90 extrasolar planets with known radii less than 4RE whose masses have been measured or constrained using radial velocity or TTV methods. Neither unconfirmed planets nor circumbinary planets were considered to keep the sample as homogeneous as possible. The team also truncated the mass distribution to physically plausible values that were no less than zero (since it is physically impossible to have a negative mass) and no greater than the mass of a planet composed of iron (since it is unlikely for a planet to have a composition dominated by any element denser than iron).
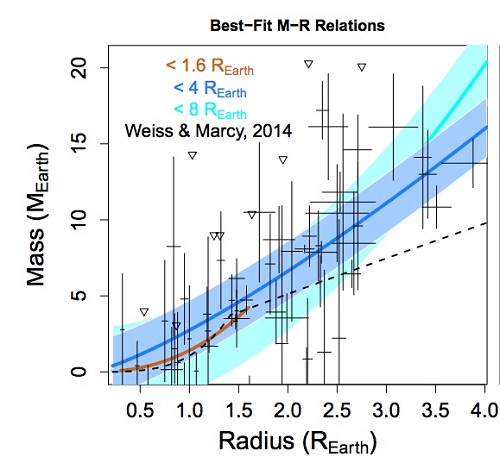
Image: This plot shows the available mass and radius data (and associated error bars) used in the latest analysis of the mass-radius relationship for sub-Neptune size planets. Various fits to these data are shown including an earlier analysis by Lauren Weiss and Geoffrey Marcy (black dashed line) as well as fits for radii <8 RE, <4RE and <1.6RE (solid colored lines). (credit: Wolfgang et al.)
The detailed analysis of the dataset by Wolfgang, Rogers and Ford found that the subset of extrasolar planets whose masses were measured using the TTV method has a definite bias towards lower density planets. This bias had been suspected since a low density planet will have a larger radius than a denser planet with the same mass. And all else being equal, a larger planet is more likely to be detected using the transit method than a smaller planet. When only considering the sample of extrasolar planets with masses determined using precision radial velocity measurements, this team found that the best fit for the data set was a power law with C = 2.7 and γ = 1.3 (i.e. M = 2.7R1.3). Based on their statistical analysis, Wolfgang, Rogers and Ford found that the data were consistent with a Gaussian or bell-curve distribution of actual planet masses with a sigma of 1.9ME at any given radius value. Just as has been suspected, planets with radii less than 4RE display a range of compositions that is reflected as a fairly broad distribution of actual mass values.
In earlier work by Rogers, it was found that there seems to be a transition in planet composition at a radius no larger than 1.6 RE, above which planets are unlikely to be dense, rocky worlds like the Earth and much more likely to be less dense, volatile-rich planets like Neptune (see The Transition from Rocky to Non-Rocky Planets in Centauri Dreams for a full discussion of this work). For the sample of planets considered here with radii less than 1.6 RE, the team found that C = 1.4 and γ = 2.3. Unfortunately, the sample considered by Wolfgang, Rogers and Ford has little good data for planets in this size range and the masses with their large uncertainties tend to span the full range of physically plausible values. As a result, this analysis can not rule out the possibility of a deterministic mass-radius relationship where there is only a very narrow range of actual planet masses for any particular radius value. Recent work by others suggests that these smaller planets tend to have a more Earth-like, rocky composition which could be characterized with a more deterministic mass-radius relationship (see The Composition of Super-Earths in Drew Ex Machina for a discussion of this work).
This new work by Wolfgang, Rogers and Ford represents the best attempt to date to determine the mass-radius relationship for planets smaller than Neptune. While more data of better quality for planets in this size range are needed, it does appear that sub-Neptunes can have a range of different compositions and therefore possess a range of mass values at any given radius. This new relation will be most useful to scientists hoping to get the maximum benefit out of the ever-growing list of Kepler planetary finds where only the radius is known. Much more data will be required to determine more accurately the mass-radius distribution of planets with radii less than 1.6 RE and more precisely characterize the transition from large, rocky Earth-like planets to larger, volatile-rich planets like Neptune.
The preprint of the paper by Wolfgang, Rogers and Ford, “Probabilistic Mass-Radius Relationship for Sub-Neptune-Sized Planet”, can be found here.



Great stuff, thanks ! I think it is amazing that barely twenty years on from the first discovery of exoplanets that such precision work can be published. Far from complete , but when you think that exoplanet astronomy is still very much the baby of the subject and that Kepler is the only substantial dedicated project in the field ,that’s no mean achievement. The resource devoted to this area has been far from substantial ,though this has led to innovation aided especially by potent processing power and quality simulation. Expect things to move forward apace over the next fifteen years as missions and equipment dedicated to constrain such parameters direct in a far larger sample size come on line. ESPRESSO, CHEOPS and TESS in the next three years alone will really start that process to be followed by the ELTs and finally PLATO next decade ,leaving us with a huge number in the sample size and an accurate awareness of boundaries between planets , the most common seemingly , of this size. Gaia ( hopefully extended to near ten years ,consumables and budget allowing ) in combination with direct imaging WFIRST will also hopefully give the first precision values through the field of astrometry at last , at least on close by planets though that should still be a fair sample in the posited 32 light year or so radius.
I hope I am not alone in lamenting the lack of a mission to Neptune (and/or Uranus ) itself , right on our doorstep in effect , to look at relatives of the planets first hand as I’m sure they especially have much to disclose in this field . Can’t see it happening , limited budgets and ice moons understandably allowing , though the ELTs will help with their far greater light gathering , spectroscopy and angular resolution .
I’d find that graph a lot more informative if the vertical scale was density
I’m not sure I buy the best fit for the <1.6 Me curve. Looking at figure 4 (left and right) it looks like the curve doesn't capture the data points well when eyeballing it as a "sanity check". Given the uncertainty in size must increase with decreasing planetary mass, I would have expected the Bayesian model to have quite wide bounds at the lower planetary masses. (Fig 4 Right: "The blue region now corresponds to the central 68% of planet masses that were drawn at a given radius." – note the constriction of the bounds starting at 1.2 Me and becoming very narrow at 0.75 Me).
Their discussion suggests that some of the mass constraints have determined the bounds.
Their values for the power gamma as less than 3 , which is what one might expect from a rocky world (and which works reasonably well for the 4 rocky worlds in sol system). Thus as the worlds transition from rocky to Neptunian, wouldn't we expect the best fit curve to be more convex, rather than concave? (Neptune/Earth gamma ~= 2).
@Andrew Palfreyman May 22, 2015 at 16:13
“I’d find that graph a lot more informative if the vertical scale was density”
Well, not to put too fine a point on it but it is an illustration for a paper about the “mass-radius relationship”. Although I certainly agree for some applications (e.g. more clearly visualizing differences in bulk composition), a plot of mass or radius-versus-density would be more appropriate.
Hi Drew and thanks for this article – glad to know about the statistical state of play in exoplanet studies.
I have a couple of question about regarding stellar metallicities.
1) From the article “This bias had been suspected since a low density planet will have a larger radius than a denser planet with the same mass.” If there is indeed a bias towards lower density planets, then wouldn’t this bias also show up by us tending to find more exoplanets found around older, less metallic stars? Are you aware of any evidence for this tendency?
2) As the article says, although “this analysis can not rule out… a very narrow range of actual planet masses for any particular radius value.”, would that not be a very surprising result, considering how much abundances of heavy elements varies from system to system?
Thank you for bringing this difficult study to our attention. Bringing some true scientific quantification on the present level of uncertainty does seem of real value. Come on TESS!
@Lionel Ward May 23, 2015 at 6:11
To address your two questions:
1) The bias I was talking about is a detection bias, not an intrinsic tendency towards lower density planets in the sub-Neptune size range as a function of any stellar properties. As I mentioned in the essay, astronomers have suspected for a while now that the planets discovered using the transit method and whose masses have been characterized using TTVs will tend to lower density planets because higher density planets of the same mass will produce a smaller transit signal that is more difficult to detect. This suspected detection bias of the combined transit-TTV method seems to be borne out in the new analysis.
It has been observed that there is a tendency for stars with higher metallicity to have more gas giants (which would have R>4RE) which have lower density, but that is a different issue unrelated to the planets in the size range being discussed here.
2) An earlier analysis of Kepler results by Rogers found that planets with R<1.6RE are more likely to be rocky planets. There is no evidence for a correlation between the radius where this transition in composition takes place and any property of the star it orbits since this is an issue related to the properties of the planet itself (i.e. if the rocky core of the planet is not massive enough to hang onto a H-He atmosphere, it will end up being a rocky planet no matter how much H-He is available during its formation). And as is discuss in "The Composition of Super-Earths", the intrinsic variations in the relative amounts Fe-Si-Mg observed in stars with planets result in only a narrow range of variation in density resulting in a more deterministic-type of mass-radius relationship in the R<1.6RE size range.
Thanks for the comment and I hope I have answered your questions.
Drew, many thanks for your reply and the details you shared. Your answers have answered my questions as I put them, although given the information you gave, it’s clear that I have phrased my first question incorrectly! When I asked whether we would tend to “find more exoplanets found around older, less metallic stars” I was of course not considering how low metallicity affects the rate of planet formation itself. I’d like to reply to your answers to my two questions below, and there’s also something else I’d like to ask about that ~1.6R_E sub-Neptune transition.
1) I will try and rephrase my previous question here – for a planet with fixed mass m, for fun, say m=10M_E, as we decrease the metallicity of that planet’s host star (in our hypothetical simulation), wouldn’t we expect to see that planet become less dense, meaning it has a larger radius, and is more easily detected by us?
(a dual question would be: “for a planet with fixed radius r, with lower metallicity in the star, then wouldn’t it have lower density?”)
2) If I have understood your reply to my second question correctly, at least in the sub-Neptune range, the Fe-Si-Mg composition of planets may only cause a small variation in density. This is interesting and surprising to me. It’s suprising because I had some recollection that in our solar system, for certain comparably sized bodies in comparable environments, there is substantial variation in density. The two examples that strike my eye from looking at Wikipedia are that the density of Callisto is 1.8344 g/cm^-3 (Ganymede’s is similar) whereas Europa density is 3.013. On a much larger scale, Neptune’s density is 1.638 while Uranus’s is 1.27. These bodies were of course formed from the same disk, and to me the differences in densities seem quite substantial. Given the range of stars and planet-forming disks out there, I would have thought that a significantly wider range of densities for each planetary mass band could exist, compared to than what’ve seen in our solar system. I’m very interested to hear whether or not this is likely given current exoplanet science.
3) On a separate topic – has there been work looking into a temperature relation for the likely 1.6R_E transition between rocky and gassy planets suggested by Rogers’ work? My assumption here is that closer towards the star, the hotter the planet, and the higher that transition between rocky/gassy planet transition might become, because more gravity is required to hold on to more energetic H/He. Concretely, would we expect the same transition for planets at 0.2AU versus at 2AU versus at 20AU?
Many thanks for dealing with my questions
I have always thought it to be little short of miraculous that exoplanets are being detected, and even imaged directly in some cases, using *existing* telescopes fitted with advanced optical sensors. Not many years ago, it was confidently (but pessimistically) assumed that exoplanets could be discovered only by actually sending starprobes or starships to the stars, or maybe by observing the nearer stars with large telescopes set up on the Moon. Also:
This article raises a question. Is Jupiter a rather anomalous planet? I admittedly haven’t kept up with the tally of known exoplanets, but from what I have read, gas giant planets that are found orbiting other stars seem to be considerably more massive than Jupiter, or are considerably smaller (i.e., like Neptune). While more massive (than Jupiter) planets are easier to detect because they cause greater “wobbles” in their parent stars’ motions, it would seem that the other exoplanet detection methods (such as the transit method) could detect “Jupiter-mass Jupiters” orbiting other stars. Have any reasons for their apparent paucity been theorized (or even hypothesized), and if so, what are they?
Many thanks in advance to anyone who can help!
@Lionel Ward May 24, 2015 at 19:03
A new day and a fresh set of questions to ponder :-) Here we go:
1) Given the paucity of data that’s available today, I don’t think it is possible to answer your question at this time (I am certainly unaware of any studies performed that addressed this specific question). Regardless of whether or not the metallicity of the host star plays any role the density of its non-terrestrial planets, current work does demonstrate that these worlds do display a large range of densities regardless of metallicity. Maybe metallicity is one of the variables in this mix but we will have to wait to get much more data to find out.
2) Well, Neptune and Uranus have radii >1.6 ME and are most definitely not terrestrial planets so their density is not expected to fall along the contour of density consistent with a rocky, Earth-like composition. The point you raise about the icy moons of the outer planets does, however, brings up a good point about the limitation of the studies performed to date. Virtually all of the planets involved in studies of planets with radii <1.6 orbit well within the "snow line" of these systems unlike the icy moons of our solar system you mention. It will be interesting to see what happens with the density trend when extrasolar planets orbiting well outside the "snow line" are included. I would expect such worlds to have a much lower density owing to the increased amount of ice they would surely have. Unfortunately, these planets are difficult to detect using the transit method and especially the RV method. It might be a while before we spot enough of these planets to make any meaningful analysis.
3) In her original paper on the subject, Rogers specifically analyzed her data to see if the radius where the transition from predominantly rocky to volatile-rich planets was affected by the mean stellar flux. Her sample included planets with 1.1 to 3700 times the flux of the Earth but she found "no statistically robust evidence for an incident-flux dependence in the radius threshold". If I were a betting man, I would suspect that a weak dependence may eventually be found especially at very high flux levels once much more data become available. Unfortunately, Kepler data do not allow much to be said about planets in larger orbits with much lower flux because the probability of detecting three transits quickly drops to zero (primarily due to the limited time of the mission) and the RV method is typically not sensitive enough to measure the mass of these worlds.
SO, I hope I was able to answer you questions once again! :-)
@J. Jason Wentworth May 25, 2015 at 4:44
To answer your question: “Is Jupiter a rather anomalous planet?”… in terms of mass, no. Statistical studies of planets found to date using precision radial velocity and transit methods do not find any evidence that Jupiter-mass planets are anomalously rare. After selection effects for various surveys are taken into account, there are clearly more Jupiter-mass planets than super-Jupiter-mass planets, more Neptune-mass planets than Jupiter-mass planets and more super-Earth-mass planets than Neptune-mass planets. Things get a bit murkier with yet smaller planets because of the paucity of data but there is every indication that there are more Earth-mass planets than super-Earth-mass planets as well.
The perception that there might be more larger planets than smaller planets when looking at the list of extrasolar planetary finds is an illusion caused by the fact that larger planets are easier to detect than smaller planets, all else being equal. When the effects of this selection bias as a function of planet size are taken into account in detailed statistical studies of extrasolar planetary populations, this “illusion” disappears.
I hope this answers your question,
@Lionel Ward:
with regard to your questions nr. 1):
If I get you well, I think there is a misunderstanding here;
This article deals purely with the relationship between mass and radius (and hence also density and radius) for planets, regardless of stellar characteristics, such as in particular metallicity.
I think it is not right to state that a lower metallicity star results in lower density planets, or that for a same mass planet a lower metallicity star would have a lower density planet. I don’t think it works that way.
On the contrary: lower metallicity among stars seems to result in smaller rocky cores resulting in smallish planets that are not able to hold on to a significant H/He envelope. And vice versa: high metallicity results in large rocky cores resulting in true gas giants. As Andrew LePage mentioned above, a rather strong correlation has been found between metallicity and the occurrence of gas giants, with a threshold value below which gas giants seem to be absent.
Indeed it does answer my question, Andrew LePage–Thank You! The “Hot Jupiters” also no doubt pop up more commonly simply because, being close to their parent stars and orbiting them rapidly, transit exoplanet searches catch them more quickly.
If we look at the transit method, how good is it at detecting actual gas giants, I mean a gas giants size compared to a red dwarf is substantial, it is likely to just graze the disc as seen from earth as cause a maximum dip in light. A partial transit could be seen as a smaller planet when in fact it is much larger, I am not sure how they could tell the difference.
@Michael May 28, 2015 at 15:34
Well first of all, gas giants orbiting red dwarfs are rare. But assuming we have a Jupiter-size planet orbiting a red dwarf with about half the radius of the Sun, a full blown transit (where the entire disk of the planet transits the disk of the star it orbits) is around five time more likely than a grazing transit. But astronomers analyzing transit events have ways of determining how far off center a transit is or if it is a grazing transit. One indication is the length of the transit – off center transits are shorter than perfectly centered transits for a given set of orbital parameters. Also, since stars display some degree of limb darkening (i.e. their disks are not evenly illuminated and are noticeably darker at the edges than at the center) and the degree of limb darkening is dependent on wavelength, the shape of the transit observed at different wavelengths as a function of time allows astronomers to gauge how far off center a transit event is. Combining detailed analysis of the shape of transit events as a function of time and wavelength with the timing parameters of the transits allows astronomers to fairly accurately gauge how off centered a transit is (a metric called the “impact parameter”) and recognize grazing transits.
Thanks Andrew
I found this article to explain the technique in more detail.
http://zuserver2.star.ucl.ac.uk/~ingo/Lecture_Notes_files/lect11.pdf
If we ever move out of the solar system with colony ships or interstellar probes just their movement and observation of transits will enable us to see a great many more as the angles change.
@Andrew LePage
Thank you and apologies for my severe latency in replying! I read your answers three weeks back when you wrote them, but haven’t managed to reply until this evening. Thank you very much your replies, which very much answered my questions.
On the metallically-density relationship, it sounds like we’ll have to wait for a lot more terrestrial planet discoveries with mass and radius calculations to know whether there’s any relationship. I was originally thinking along the lines of “surely if we discovered a 1 R_E planet around another star, then it’s expected mass would be lower if the star’s metallicity is 1/4 of Earth’s vs. if it’s 4x Earth’s?”; but it seems that we are unable to say anything about such a relationship so far, and my intuition may be wrong.
I very much take the point about higher metallicity increasing the abundance of terrestrial worlds. At the ‘zero extreme’, the oldest stars in the universe (apparently known as Population III) would not have any rocky planets because the disks they formed from consisted virtually other than hydrogen and helium and trace lithium from the big bang. (I heard this in one of Prof Brian Koberlein’s (Rochester Institute of Technology) recent podcasts – totally obvious once hearing it, but I must admit that I hadn’t realised prior to that)
Very interesting about the flux vs. rocky-gassy transition as well – another reminder of the massive bias in our data towards hot inner worlds.
@Ronald
Thanks for your comment. While I get it that the major upshot from lower metallicity that fewer rocky worlds are seeded, I think it still is meaningful to think about what variables will change what mass we expect from the exoplanets we discover. As in the example I made above – say we’ve just found an exoplanet of one Earth radius, are there any variables that modify the mass we expect it to have? If it’s around a star with five times the relative abundance of heavy elements compared to our Sun, then is our best guess of said exoplanet’s mass going to be unchanged at 1 M_E?
@Lionel
‘Metals’ were produced quite quickly after the formation of the first stars at least locally. Very large quantities of materials, dust included, are expelled from the large early stars even before they go out with a bang.