Deceleration has always been problematic in projected schemes for interstellar travel. A flyby of a star at a substantial percentage of lightspeed yields a fraction of the data that would be obtainable by a probe slowed into orbit in the target system. But how to slow down? In particular, how do you slow down when your method of propulsion is beamed energy?
The ideas have flowed over the years, ranging from Philip Norem’s ‘thrustless turning’ — using interactions between the spacecraft and the interstellar magnetic field — to Robert Forward’s ‘staged’ sail, in which the sail separates into separate components, with beamed laser light from Earth bouncing off one to the other to slow the payload. Norem’s notion, though, hugely lengthened trip times while taking the spacecraft far beyond the target before turning it back, while staged sails require a pointing accuracy in a laser array that is hard to imagine.
Many other options have been advanced, including braking against a stellar wind with a magsail, but it was a recent paper from René Heller (Max Planck Institute for Solar System Research, Göttingen) and German colleague Michael Hippke that got my attention at the beginning of February (see By ‘Photogravitational Assists’ to Proxima b). Heller and Hippke are now joined by Pierre Kervella (CNRS/Universidad de Chile) in a reworking of the original idea with a major twist, a far more effective means of slowing and turning the craft which, in turn, produces much faster travel times because it allows a higher speed upon arrival.

Image: Orbital plot of Proxima Centauri showing its position with respect to Alpha Centauri over the coming millennia (graduations are in thousands of years). The large number of background stars is due to the fact that Proxima Cen is located very close to the plane of the Milky Way. Credit: P. Kervella (CNRS/U. of Chile/Observatoire de Paris/LESIA), ESO/Digitized Sky Survey 2, D. De Martin/M. Zamani –https://www.eso.org/public/images/ann16089a/
Photogravitational Assists and Lightsails
The original Heller/Hippke paper fit nicely with the Breakthrough Starshot idea, in that what the latter was proposing was to accelerate small beamed sails up to 20 percent of the speed of light for a flyby of the Proxima Centauri system and its interesting planet Proxima b. Hippke and Heller advocated using the G-class Centauri A and K-class Centauri B as ‘photon bumpers,’ with a much larger lightsail than Breakthrough Starshot envisioned being slowed and having its trajectory altered by photon pressure and gravity, with a final deflection to Proxima Centauri itself, which the craft would approach at a speed slow enough for photon braking into orbit.
The new paper finds a more efficient way of using a star as a photon bumper, one that increases the deceleration at Centauri A and B and thus allows the sail to approach these stars faster. The savings are substantial: Using a modified photogravitational assist as suggested here, we cut the travel time from 95 years to 75 years. You can see that to use these methods, a single star is not optimum. We look instead for multiple systems in which we can use two or more stars to pull off this interstellar bank shot. Intriguingly, it turns out that the Alpha Centauri system may not actually be the closest — in time — for such a mission, but more on that later.
The spacecraft that Heller, Hippke and Kervella have in mind is made of an ultralight material like graphene, which would be coated with “a highly reflective broadband coating made of sub-wavelength metamaterials.” For a Centauri mission, the craft would be brought up to cruise velocity by a close solar pass rather than accelerated through a ground-based laser array, the method being investigated by Breakthrough Starshot. The lightsail would be accelerated to a cruise velocity of 4.6 percent of c. It would use the assist maneuver upon arrival at Centauri A and B and brake into Proxima to achieve a bound orbit around Proxima b.
When using the photon pressure of a star and its gravitational pull to both decelerate and deflect an incoming sail, the key is to find the maximum possible injection speed at the first destination star. Doing that at Alpha Centauri A would allow the necessary flyby and course adjustment at Centauri B, followed by deflection to Proxima. Finding that injection speed has to be factored against reaching the required deflection angle between inbound and outbound trajectories.
The new work introduces follow-up studies to the Heller/Hippke paper that tweak the simulations with a revised concept, one that favors stellar photon pressure over gravity in enhancing the deflection. The result: “we demonstrate that such a photogravitational assist is more effective when the star is used as a bumper (i.e. the sail passes “in front of” the star) rather than as a catapult (i.e. the sail passes “behind”or “around” the star).”
From the paper (note that v?,max, as discussed below, is the maximum speed of arrival for a successful deceleration and deflection within the Centauri system) :
From a geometry perspective, it is more efficient to let the sail approach the star on the same side (e.g. on the left, see Figure 1) as the desired deflection (i.e. to the left). We then find that, using the same optimization strategy for deceleration as Heller & Hippke (2017), a maximum total deceleration of v?, max = 17, 050 km s ?1 can be reached at ? = 19° , where 8, 800 km s ?1 and 8, 400 km s ?1 can be lost at A and B, respectively.
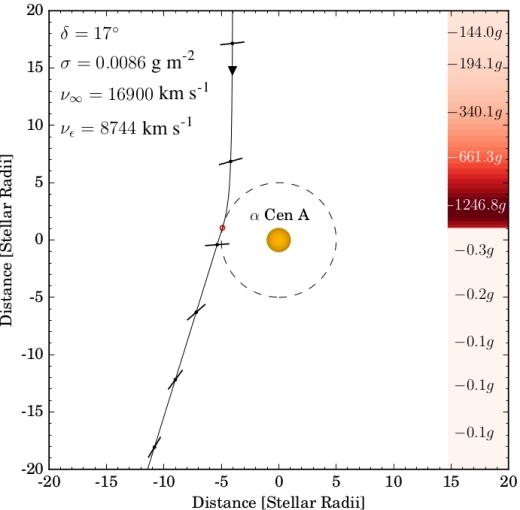
Image: Figure 1 from the paper. Caption: Trajectory of a lightsail performing a photogravitational assist at ? Cen A (orange circle). The bar along the trajectory visualizes the instantaneous orientation of the sail determined to maximize the deceleration. The values in the legend denote the deflection angle, the mass-to-surface ratio, the inbound velocity, and the outbound velocity of the sail. The color bar at the right shows the g-forces acting on the sail along the trajectory, where g = 9.81 m s ?2 is the acceleration on the Earth’s surface. Credit: Heller, Hippke and Kervella.
The revised work thus changes the original Proxima b mission. Assuming the intent is to brake into the Proxima system for close examination of the planet, then the sail is better oriented so as to avoid maximum deceleration during its encounter with Centauri B. This allows the cruise to Proxima to continue with a residual speed of 1,270 km s-1, which is the maximum speed that can be used to fully brake into the Proxima system. As you can see, the authors must juggle the fastest possible cruise times with the maximum injection speeds.
So we have learned that when the photogravitational assist is made at the same side of the star as the desired deflection, as opposed to a gravitational swing behind the star (the method of the original paper), the injection speed at Centauri A (and thus cruise speed enroute) is increased substantially. The authors’ calculations involving a graphene lightsail show an injection speed (v?, max) of 17,050 km s-1 for the new method (this works out to 5.7% c, as opposed to the previous 13,800 km s-1, which is 4.6% of c). We get an increase in speed of 24 percent, while we reduce travel times from Earth to Centauri A and B from 95 years to 75 years.
Adding in the travel time to Proxima Centauri after the photogravitational assists at Centauri A and B, we get a total travel time from Earth to a bound orbit in the Proxima Centauri system of 121 years, with the final 1,280 km s-1 absorbed through photon braking at Proxima itself. 46 years, in other words, is needed to go from Centauri AB to Proxima. What a shame we can’t launch such a mission this year, for the alignment in the Centauri system is such that a mission arriving at Centauri AB in 2092 would allow minimum travel times and maximum injection speeds. In 2092 the deflection required by the sail for the AB photogravitational assist is smallest.
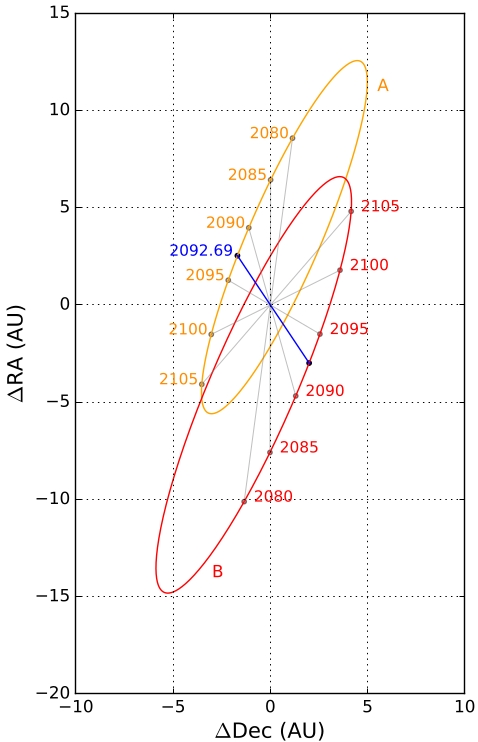
Image: Figure 2 from the paper. Orbital trajectories of ? Cen A (orange) and B (red) in their barycentric coordinate system as seen from Earth using differential RA and Dec coordinates. The AB vector at the time of their closest apparent encounter in 2092.69 (8 September 2092) is marked in blue. Credit: Heller, Hippke and Kervella.
It should be clear from all this that to calculate the actual value of the maximum injection speed at Centauri A and B, we need to calculate the deflection angle required by the sail to make the necessary trajectory adjustments. This will be the case in any nearby system to which we hope to apply these methods. And here we find the interesting result that there are systems which could be closer in terms of travel time than Alpha Centauri itself. Tomorrow we’ll return to this paper to look at the possibilities for photogravitational assists to bound orbits in other systems.
The paper is Heller, Hippke and Kervella, “Optimized trajectories to the nearest stars using lightweight high-velocity photon sails” (preprint).



I am on board a very large and massive worldship , we are traveling much slower than this.
what would be the max speed to slow us down from in multiple star systems utilizing just ballistic astrodynamics?
Vernor Vinge did a computation like that for the Alpha Centauri system. I think the top speed was about 110 km/s. A slow trip.
I found a calculator
http://www.unitjuggler.com/convert-speed-from-kms-to-c.html?val=100
does not help me with TOF
I found on a blog that 50 Km/s is 23,000 years to Alpha Centauri, so 100 Km/s would be half of that?
A world ship that could add and then subtract another 100 Km/s from its great mass might make this idea more feasible
200 Km/s outbound 200 km/s subtracted inbound,
5000 years TOF ?
Alpha Centauri is about 4.3 light years away. That means that a photon travelling at 1c will take 4.3 light years to cross that distance.
To calculate how long it would take at 100km/s, first divide by 300,000km/s to figure out what fraction of c that is. You get 1/3000 c, or in other words 1 light year per 3000 years.
4.3LY divided by 1LY/3000Y is around 130,000 years.
For comparison, I suggest an alternative method which could let you use a cruise speed of 700km/s, or 7/3000 c. That gives a travel time of around 1,800 years.
So had the Romans launched a probe in their 2md or 3rd century CE, we might be getting some results about now. ;)
Interstellar travel that requires feedback to Earth is not really going to work on these timescales. One-way travel, e.g. in a sleeper ship might be fine.
While we have discussed long mission times before, I don’t think scientific missions lasting longer than a human lifetime make much sense. Either the probes have to go faster, or human lifetimes extended. Harvesting radiation that has already traveled the distance to the solar system makes more sense for a scientific or engineering career.
Even today functioning space probes are shut down because they’ve outlived their scientific usefulness. I suspect it is this (rather than technology or human lifespans) which will limit mission times. Science will change so radically in a century (to say nothing of a millennium) that there is little likelihood anything we launch now will be of value that far in the future. A possible solution is to hedge our bets, sending out probes that return data useful to us in the short to medium term, but which will continue to function if our descendants decide it is worthwhile to keep them operational.
“That means that a photon travelling at 1c will take 4.3 light years to cross that distance.”
No. A photon experiences no time duration at all. Think about it. Your following examples only work because v << c.
Thanks, for the formula!
Unless the stars are in a close binary orbit you more or less don’t get any free braking. The speed in equals the speed out, more or less.
You can take advantage of the Oberth effect to assist deceleration near the star, but the effectiveness of this technique is limited by how much delta-v your rocket system can handle. Figure an escape velocity around 400km/s (maybe up to 600km/s if you’ve got a great heat shield), and you can calculate the Oberth effect benefit as:
sqrt((400km/s+dv)^2-(400km/s)^2)
For example, if you are using a thermal hydrogen rocket powered by the solar heat shield, then you might have a delta-v of 10km/s. This gives you an incoming velocity of sqrt((410km/s)^2-(400km/s)^2) = 90km/s.
Frankly, 90km/s is not that great, but it’s an order of magnitude better than 10km/s.
A more powerful possibility is to use kinetic impact powered propulsion, and to release a bunch of sacrificial impactor drones well before arrival. The impactors and the main starship travel nearly parallel, but headed toward opposite sides of the destination star. They both swing in hyperbolic paths so they impact behind the far side of the star. This can result in impact velocities on the order of 1000km/s, suitable for braking from perhaps a 700km/s cruise velocity (accelerated to around 900km/s at periapsis).
A 700km/s cruise velocity may be more like the sort of velocity you’re hoping for.
Naturally, if you want the impacts to merely decelerate the starship rather than destroying it, you need to do something like have them impact a huge direct impact shield (which gets cratered like crazy) or puff a fluid to vaporize the incoming impactors so they turn into plasma that gently pushes a pusher plate.
Note that because the impacts aren’t head on, the starship will still end up with a large velocity away from the destination star. As long as this is below escape velocity, though, the starship will end up captured into an elliptical orbit.
Just bought a Scientific American off the shelves at Fry’s Grocery. The cover story for this issue is an effort to send a probe to Alpha Centauri.
Geoffrey Landis is part of the team as is Freeman Dyson. Landis talked about how the sail could be pulled in some to form a parabolic high gain antenna to send data back to earth. Although that might reduce the sail’s ability to brake.
But it sounds like they’re thinking of a fly by so inability to brake wouldn’t be a show stopper.
I think you’re talking about Breakthrough Starshot. Numerous articles in the archives here about it, including my coverage of their last two meetings. But I haven’t read that issue of Scientific American yet…
https://www.scientificamerican.com/article/inside-the-breakthrough-starshot-mission-to-alpha-centauri/
I skimmed the paper and I don’t feel much enthusiasm about this method of deceleration. It works, with many ‘buts’.
The overwhelming share of the deceleration is due to light pressure. The A Cen maneuver works because the very very slight deflection allows two stages of light pressure deceleration from the two primaries. In Sirius’ case light pressure is pretty much the entire show due to its far higher luminosity.
The technique is more suited to multiple star systems, should those prove of interest. The deceleration is almost 100% light pressure with the gravitational deflection increasing the deceleration stages.
Also, note the deceleration forces. They are extreme, as one should expect with these high velocities. The same would apply on launch acceleration. All this is nothing new.
I think we can be satisfied with exploring the Centauri system for the time being.
Unfortunately, this concept doesn’t work. Or more accurately – it does work better than gravity, but nowhere near as good as the paper calculates. They make a mistake by assuming an areal density of a single layer of graphene but not taking into account the fact that a single layer of graphene is very transparent (it only absorbs 2.3% of the incident light).
As a result of this error, they overestimate the potential acceleration by two orders of magnitude. The result is still a lot better than gravity, but not useful for practical interstellar mission speeds (with current human lifespans). We’re talking speeds suitable for travel times of many thousands of years.
The claims made by the paper instantly hit “red flag” territory for me because I had already been analyzing the potential performance of graphene sails for my SF web comic. It’s actually really good for my purposes since the mission in my webcomic is only to a destination 550AU away (the sails are used indirectly via kinetic impact powered rocket propulsion similar to mag-Orion but with much smaller non-nuclear plasma explosions).
When I first did my analysis, I made a similar error involving some zeros…in my case, it was because I forgot the difference between grams and kilograms. But the result was similar. I had a “wow” moment, but then I pored through my calculations again until I found the error.
Now, the reason I had skepticism that time around, was because I had previously years ago analyzed the potential of graphite sails, and I was not expecting graphene to outperform that by so many orders of magnitude (it does not, in fact outperform graphite by an order of magnitude – but it’s still quite a bit better and there are many advantages to graphene over graphite).
There is no mistake. You are reading it wrong. In the abstract they say:
“This increases the maximum deceleration at ? Cen A and B and reduces the travel time of a nominal sail with a mass-to-surface ratio (?) similar to graphene (8.6 × 10?4 gram m?2 ) from 95 yr to 75 yr”.
Note they say “similar” to graphene, not “the same” as graphene.
Below in the article they describe the sail they will use:
“Assuming that the sail would be made of a strong, ultra-light material such as graphene, which would be covered by a highly reflective broadband coating made of sub-wavelength thin metamaterials (Slovick et al. 2013; Moitra et al. 2014), such a sail could have a maximum speed at arrival (v?,max ) of about 4.6 % c to be successively decelerated at the stellar triple ? Cen A, B, and C (Proxima)”.
That is, they will use a graphene monolayer covered by a silicon-based monolayer, according to the reference, which will have “normal-incidence reflectivity over 99.999% and absorptivity less than 0.001% at a short-wave infrared wavelength of 1.5 ?m.”
Yeah, that’s something they added on but it doesn’t work at all. Silicon doesn’t have the high melting point of graphene, so it’s just wishful thinking to hope that this magical material will be capable of withstanding the high temperatures graphene could handle.
And this idea that somehow magically a this two layer material could have an extremely high reflectivity with low absorptivity? That’s really magical thinking. With many layers, it’s possible for dielectric layered mirrors to have high reflectivity with low absorptivity, but with just two layers? No…sorry, no. Most of the light will pass through the layer and 2.3% of the rest will be absorbed by the graphene.
And even a single layer of silicon ruins the low areal density assumed (which matches single layer graphene). A many layer dielectric layer would completely kill the areal density.
It actually makes more sense to simply go with multi-layer graphene (or just a single layer of graphene and accept the lower photon pressure). But in any case, the acceleration level is going to be a couple orders of magnitude lower than what they hope.
The most charitable reading of their paper is to go with the original which is just graphene. The stuff they added to handwave around the original mistake is just intellectually embarrassing.
“That’s really magical thinking.”
Then why it was published in Physical Review B and Applied Physics Letters? Hurry, tell the referees that they let pass magical thinking!
Eh, having reviewed a lot of arXiv papers, there’s a lot of mistakes and misinterpretation of referenced papers. Not that there aren’t lots of mistakes in scientific literature in general, but I’m speaking of arXiv specifically only out of familiarity.
I’m not sure what, precisely, is the reference you are talking about, but the ones I saw in the arXiv paper seem to be about metamaterials with high reflectivity but NOT atomic thickness. They make the assumption that what they hope for is possible, in order to salvage the rest of the paper, but there’s no compelling reason to expect this is possible.
Look. There’s nothing wrong with an interesting paper studying the possibilities of X assuming Y is possible. But this doesn’t mean we can expect Y to be possible.
The reference was very clear from my comment:
“Assuming that the sail would be made of a strong, ultra-light material such as graphene, which would be covered by a highly reflective broadband coating made of sub-wavelength thin metamaterials (Slovick et al. 2013; Moitra et al. 2014), such a sail could have a maximum speed at arrival (v?,max ) of about 4.6 % c to be successively decelerated at the stellar triple ? Cen A, B, and C (Proxima)”.
Sorry, but there is not just one reference in that comment. That already makes it ambiguous. There’s one from 2013 and one from 2014.
Neither of those references demonstrate that the assumed material with the desired assumed thinness is possible, so I thought maybe you were talking about another reference.
They do demonstrate it, say so in the abstract and are peer-reviewed. We could discuss whether water is wet, and you could repeate forever that it’s magical thinking, but I have better things to do.
Seriously, no. The 2013 paper has to do with reflecting something narrow bandwidth, like a laser. The 2014 paper has to do with something broad band but with much inferior characteristics than the assumed material. Both are strictly theoretical in nature also.
The truth is, the original paper simply talked about graphene. Plain old graphene. Which might not be the best possible material, but it’s one which we have good real world lab data on.
https://arxiv.org/abs/1701.08803
This additional magically hopeful mashing up of hypothetical materials to get something that salvages the original paper is intellectually sloppy and embarrassing.
I gave you the benefit of the doubt by guessing you might have been talking about some other paper other than one of those two. But if we’re talking about those two? They just don’t say what you think they say. The authors of this paper make a magically hopeful assumption of a material which combines the best features of both of the theoretical metamaterials referenced. The fact that these papers are cited does not mean that they support the claim that cites them.
A more detailed description of the sail:
“In our nominal scenario, we consider a sail made of a graphene structure (? = 7.6×10?4 gram m?2 ) with a graphene-based rigid skeleton and highly reflective coating that is capable of transporting a science payload (laser communication, navigation, cameras, etc.) of about 1 gram (Heller & Hippke 2017). Such a sail must have an area of about 105 m2 = (316 m)2 to make the weight of the science payload negligible against the weight of the sail structure. At this size, the graphene structure would contribute 76 gram, the skeleton and coating could add 9 gram, and the payload would add another 1 gram, implying ?nom = 8.6×10?4 gram m?2 for our nominal graphene-class sail”.
1) I am quite skeptical of the usefulness of a scientific payload sharing 1 gram of mass with laser communication, onboard computers, power systems and so on. How many millimeters wide would the lens be, in the first place?!
2) The 9 gram silicon coating is interesting. It would be 28.5 milligrams per square meter, which turns out to be only 12.2 nanometers thick. How did they calculate that it would remain reflective at this thickness? This is better performance than dielectrics tuned to specific wavelengths, yet it is achieved over a broad spectrum here?
3) 76 grams accelerating at the peak 1246.8G gains 5.68MW of kinetic energy. If the silicon layer absorbs only 0.001% of this energy (wow), it must be re-emitted with an emissivity of 0.00001… 56.8W over 316m^2 translates into 0.179W/m^2 and a Stefan-Boltzmann temperature of 750K. While this is far below the melting temperature of either graphene or silicon, it might lead to some extreme thermal expansions….
(If the silicon perfectly transmits its heat to the graphene face, then the equilibrium temperature is only 42K).
1) I’m skeptical too.
2) It’s referenced in the paper.
3) The copy-paste from the PDF messed the notation up. The sail is 10^5 m^2 or (316 m)^2. Thus, it’s 56.8 W / 100,000 m^2 or 0.000568 W/m^2.
If we were flying in to Alpha Centauri rather than the “backwater” or Proxima, would the combined stellar radiation from the twin stars be enough to slow down our speeding probe, assuming it had turned its original sail around 180?
This is one of the most exciting papers on space travel I’ve ever read. The fact that I’m able to read about intragalactic navigation on timescales comparable to a human lifetime is rather wonderful.
Making monatomic graphene sheets highly reflective might just be a question of some creative doping, or perhaps an additional metamaterial layer. Since the trip time scales as the square root of the areal mass density, I don’t foresee tremendous damage being done to the broad conclusions of the paper as a result of this extra complexity.
There isn’t anything that graphene could be doped with that has the reflectivity/absorptivity per areal density of more graphene. A single layer of atoms just isn’t all that opaque, generally.
(For various reasons, a couple other interesting laser sail materials are aluminum and sapphire, as well as many layer dielectrics (based on sapphire/diamond), but neither of these are as good as graphene for a solar sail.)
A very thin layer of extremely reflective silicon-based material will be added to the graphene ‘backbone’ for the sail to be both reflective and strong.
I also have more confidence that the required sail material can be developed than that StarShot’s laser array can be built (from the funding point of view, that is). The “laser array” for this new mission idea is already there, ready to be used. Also:
The types of maneuvers they are looking at conducting could be tried in the solar system–even as close as the Moon–using prototype sail probes of this kind, while gathering “free” science data in the process.
Yes, With the development metamaterials especially in optics and nano mechanics plus nano robots many new concepts could be developed. Building the material up in the same way that we currently make advanced chips, with many of the chip developers interested in space could be the way to go. Could these be made like curtains then sewn together to make a huge sheet? The close solar pass would sound like the cheapest and easiest to develop it quickly. The ability to learn and improve the sail like integrated chips have improved over the last 50 years could also be a great advantage!
*Nods* Such integrated solar sail/spacecraft probes would be similar in basic concept to Robert Forward’s microwave-pushed Starwisp interstellar probe (although it was a fine mesh of wires–further study showed that this microwave sail likely wouldn’t work well), in that the spacecraft systems and sensors would be *part* of the solar sail, and:
Spacecraft of this kind would be well worth developing for all sorts of closer-to-home applications first (so that interstellar probe versions could leave the solar system with well-matured, “risk-retired” technologies and systems). Solar sail/spacecraft–which should be able to be mass-produced using beam-deposition and other additive manufacturing techniques–could be used in the following ways:
They could be utilized as inexpensive, fuel-less maneuverable Earth satellites and as flyby-type or orbiter-type lunar, solar, interplanetary, planetary (and/or planetary satellite), asteroid, and comet probes. Versions with sufficiently low mass/area ratios could also be used as statites (which could hover stationary above the Sun rather than orbiting it), and for orbiting in non-Keplerian orbits (orbiting above or below [north or south of] the plane of a normal orbit, for example).
I heard some where that they were contemplating a ball for the Breakthrough Starshot sail since they could keep it from being deflected in the laser beam. “The craft would be brought up to cruise velocity by a close solar pass”, how well would this work for use in the solar system? “Made of an ultralight material like graphene, which would be coated with “a highly reflective broadband coating made of sub-wavelength metamaterials.” If there going to go this far how about having the graphene gather all the Hydrogen that it will encounter in flight on its forward facing side and have a metamaterials ion nanorocket use it to slow it down?
Here’s a little study that may help us in the future to get us where we want to go.
https://www.sciencedaily.com/releases/2017/04/170417095534.htm
Not the full answer but gives us an understanding of what we once thought was theoretical.
I wonder if it’s the same thing as Robert Forward’s negative matter (not the same thing as anti-matter), where affixing two equal masses (one of matter and one of negative matter) together would–as he said–cause the pair to keep accelerating? Even if the negative mass fluid isn’t the same thing, though, this line of research is worth pursuing.
it’s NOT true negative mass …
And isn’t there the slight problem of negative mass not actually existing?
Using Sol to amplify transmissions from interstellar probes at Alpha Centauri and beyond:
https://www.digitaltrends.com/cool-tech/suns-gravity-interstellar-video/
To quote:
According to Hippke’s calculations, the gravitational lens telescope could increase data rate by a factor of one million. That would mean data transfer rates sufficient for live HD video streaming. (“Although live is relative,” he points out. “The speed of light still applies, and it takes the photons 4 years for the journey.)
The coolest part of Hippke’s suggestion is that it uses a lot of existing technology — although it still requires the use of a spacecraft being launched further into space than any we’ve launched before.
“The receiver itself it off-the-shelf established technology,” he said. “A telescope like the Hubble Space Telescope would be totally sufficient in terms of aperture and quality. It would need to be equipped with a coronagraph, also standard technology, and a fast photon detector. The difficult part is to bring the device, which would be 1 to 2 meters, to to a distance of 600 astronomical units — roughly the distance from Earth to the Sun — which takes many decades with classical rockets. However, there are some NASA studies that show options for gravitational swing-bys and high-velocity rockets to make it possible in 30-50 years.”