Breakthrough Starshot, the ambitious 30-year plan for launching small interstellar craft to a nearby star, depends critically on the sails that will ride a laser beam to 20 percent of lightspeed. In the essay below, James Benford takes a hard look at where we are now in the matter of sail stability, a subject he and brother Gregory have analyzed in their laboratory work. But as Jim points out, there is a great deal we still don’t know, emphasizing the need for a dedicated test facility in which deep analysis and experimentation can proceed. The Chairman of the Sail Subcommittee for Breakthrough Starshot, Dr. Benford gives us insight into the magnitude of the challenge, and the possible solutions now being considered.
By James Benford

Riding on the beam, i.e., stable flight of a sail propelled by beam momentum, is an essential requirement of beam-driven propulsion. It places considerable demand upon the shape of the sail and beam. Some amount of beam jitter, oscillations in the location of the beam, is to be expected. But even if the beam is steady, a sail can wander off the beam and its shape can become deformed by the high acceleration. Little of the parameter space of possible sail shapes and materials, as well as beam shapes, has been explored to date. Here I describe recent developments.
Sail Geometries
Generally, sails without structural elements cannot be flown if they are convex toward the beam, as the beam pressure would act to compress and perhaps collapse them. On the other hand, beam pressure keeps concave shapes in tension, so conical concave shapes are a possible natural answer to sailship configuration questions, essentially a circular cone. These shapes resist sideways motion if the beam moves off-center, since a net sideways force restores the sail to its original position.
Simulations show that this passive stability works, but it requires suspending the payload below the sail for a more stable configuration. This configuration is a conical shape, perhaps spinning, with the payload hanging from the apex along a tether, which may be flexible, as in Figure 1. It is shaped roughly like a parachute. (Although sails have stress distributions different from a parachute: The beam pressure keeps concave shapes of sail under tensile stress, but the periphery of the sail tends to close, so the sail needs a ring at the largest radius to keep it unfurled. This ring is under compression, and subject to elastic instability.) Such a ring may be a logical place to put the payload, which I think should be distributed to avoid single point failures. I’d much rather have it around the periphery and with some redundancy. One thing I’d don’t like about the “chipsail” idea is that having a single few square centimeter chip on a few square meter sail means that one unfortunate interstellar dust impact will obliterate the payload, losing the mission.
Simulations of conical sails showed the boundaries of sail shape and payload mass giving stability [1]. Simulations at JPL and University of New Mexico showed stability for sail shapes with the conical surface at angles from the horizontal of 25 to 30 degrees, a narrow range. Experiments have verified that beam-riding restoring forces do occur [2]. Stability also depends upon the ratio of the sail mass to payload mass. A recent analysis by Popova et al. showed analytically that stability occurs when the distance from the sail to the center of mass of the entire assembly is larger than the sail radius of curvature for small radius of curvature-L greater than D, the sail diameter [3]. These results mean that the tether must be several times the sail diameter. The mechanical oscillation modes of the tether/payload/sail that affect stability will require carefully analysis.
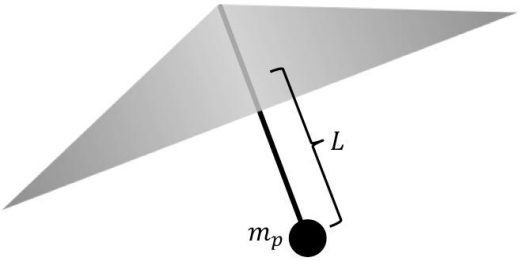
Figure 1 Conical sail with payload of mass mp hanging beneath it, connected by a tether or pendulum bob of length L (Credit: Z. Manchester).
Manchester & Loeb have suggested a spherical sail-hollow, like a shiny balloon, riding on a hollowed-out ‘donut’ beam shape [4]. This architecture has passive stability while also allowing the payload to be inside the sphere, shielded from the laser beam. That’s because it produces a potential well for the sail to sit in, which is stable if the well is deep enough. But the well in the figure is rather shallow. The sail can be inflated into the spherical shape, so could be gas-filled. This hollow beam, composed of 4 Gaussians is just one of many possible “hollow beam” geometries.
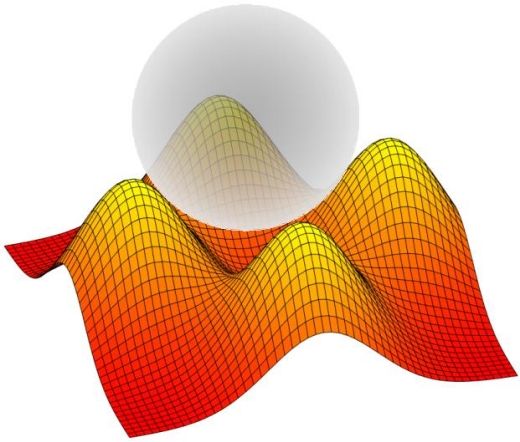
Figure 2 Multimodal beam profile composed of four Gaussian laser beams with spherical sail immersed in them. The corresponding ‘potential well’ for the transverse dynamics of a sail is much shallower than this beam intensity profile. (Credit: Z. Manchester).
From [4] I calculate that, in the example profile of figure 2, 80% of the beam power is lost to the sides of the sail in order to produce this stable regime. That would require that the power of the laser be increased to factor of 5, a huge cost which may be improved using a ring beam with no low areas, through which the sail can escape. Therefore the cost of the spherical sail-hollow beam approach is a big drawback.

Figure 3 A spherical sail will resemble this helium-filled aluminized Mylar balloon. The beam pressure can cause the beam-facing side of the sail to flatten, assuming a more hemisphere shape.
The spherical sail is an idealization akin to that of the “spherical cow” of theoretical physics infamy. In practice, material under about 10,000 g’s acceleration will not remain spherical. It will be deformed under acceleration into an oblate shape, and therefore the spherical symmetry will cease. So will the stability guarantee. The beam pressure causes the beam-facing side of the sail to flatten, so it assumes a more hemisphere shape. Such deformation of the sphere’s surface could cause significant torques on the sail, complicating analysis. This should be explored by modeling and numerical simulations.
Finally, a spherical sail maximizes cross-section to interstellar dust & gas. Compare to a shallow cone, rotated to go edge-on to the direction of travel. The spherical sail must undergo topology change to reveal the payload, and then reconfigure to become an antenna for return of data.
Modeling Sail Flight
Models of sail stability have thus far assumed a perfectly rigid sail. To deal with the many factors involved in sail stability, simulations must relax the rigid body constraint of work up to now. An example of a code geometry that has been studied in simulation is shown in Figure 4.
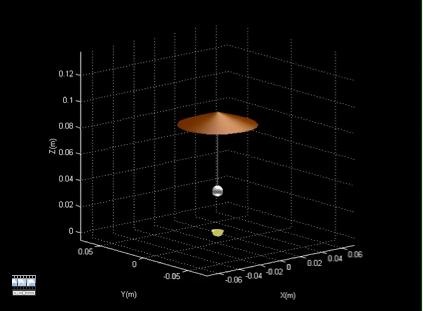
Figure 4 Simulation space for a rigid conical sail with pendulum bob payload [1]. The beamer is directly below the sail.
To address the beam-riding challenge, future simulation codes should include
- a large variety of sail shapes and beam profiles,
- multiple internal reflections,
- sail vibration modes,
- sail spin,
- simulations must include sail material characteristics including reflection/absorption as a function of angle of incidence.
Codes must also model noise in the system, arising from factors such as perturbations due to atmospheric turbulence, laser pattern variations as well as jitter in the beam and vibrational modes of the sail. While perturbations of the sail will surely excite oscillatory motion, the sail must be in a sufficiently deep ‘potential well’ to remain on the beam.
Conclusion
The parameter space of sail shape and beam shape has been studied to only a narrow, easily accessible extent. The conical sail with a payload hanging below at is the most studied and appears to have some stable regimes. But this is verified only by analytic modeling and limited simulation of the equations of motion. Mechanical aspects of the tether/payload/sail will affect stability and has not been explored. The spherical sail has been studied analytically and appears to be stable only inside a hollow beam, which substantially reduces the efficiency of propulsion.
There is much theoretical and experimental work to be done on beam-riding, an essential requirement of beam-driven propulsion. Beam-riding and sail stability analytical models have reached their limits. Computational models must be substantially improved. Such models can be validated by laboratory experiments. For such a complex problem, only experiments will be decisive.
Looking beyond the distant goal of Star Shot, beam powered sails can play a role in the coming era of interplanetary exploration and eventual commerce. The first useful beam-riding sails will come from such stability studies, which should be undertaken now. In this lower velocity and power regime the dynamics will play out. Such lessons can have great use over decades to come.
[1] D. Georgiev, E. Schamiloglu, C.T. Abdallah and E. Chahine, “3-D Simulations of Rigid Microwave Propelled Sails Using Spin”, Beamed Energy Propulsion, AIP Conf.
Proc. 664, pg. 336, A. Pakhomov, ed., 2003.
[2] G. Benford, O. Goronostavea and J. Benford, “Experimental Tests Of Beam-Riding Sail Dynamics”, Beamed Energy Propulsion, AIP Conf. Proc. 664, pp. 325, A.
Pakhomov, ed., 2003.
[3] H. Popov, M. Efendiev and I. Gabitov, “On the stability of a space vehicle riding on an intense laser beam”, Mathematical Methods in the Applied Sciences, John Wiley & Sons, Inc., 40, pp. 1346, 2016.
[4] Z. Manchester and A Loeb, “Stability of a Light Sail Riding on a Laser Beam”, ApJL 837 L20, 2017.



I wonder, James Benford signed anti-METI statement “Regarding messaging to extraterrestrial intelligence (METI)”, https://setiathome.berkeley.edu/meti_statement_0.html
and at the same time he designs “Riding on the laser beam”, which will be visible at interstellar distances?
My friend Alexander Zaitsev implies a contradiction between opposing sending messages and using power beaming to accelerate spacecraft. There is no such contradiction. The power beaming that Star Shot and others have talked about is not a message; it’s simply energy; no information is conveyed. And the Berkeley assertion he refers to simply says that we should not broadcast messages until we have had an thoroughgoing discussion involving as many interested parties as possible. Deciding to send a message is a civilization decision and shouldn’t be undertaken by individuals who do not represent the larger society. As the Berkeley statement says: “The decision whether or not to transmit must be based upon a worldwide consensus, and not a decision based upon the wishes of a few individuals with access to powerful communications equipment.”
Power beaming will be seen as a short burst of energy in the form of coherent radiation. Coherence in the source does not imply that it is artificial. There are many such a coherent sources. The most common example of naturally occurring coherent radiation are the pulsars.
Note that power beaming will not be for sending signals, but will be observable as leakage from the intense beams of radiation necessary to drive spacecraft or transfer energy over interplanetary or interstellar distances. They are far brighter than communication signals, even SETI Beacons. Therefore when we start using power beaming, it’s going to be very observable at interstellar distances. Moreover, ETI would know that their power beams could be observed. They might well imprint a message on their power beams when they know that our solar system is within their field of view of their Beamer. So power beams may be not only the most observable feature of civilization at interstellar distances, but would be the natural medium in which to embed a message. For more on this, see Seeing Alien Power Beaming, https://centauri-dreams.org/?p=34133
The main motto of David Brin and other METI-phobia people is: “Keep quiet! It isn’t necessary to appear in the Cosmos with the powerful electromagnetic radiation! It is very dangerous adventurism”, http://www.davidbrin.com/nonfiction/setisearch.html
But your transmitters will break the silence…
I would think it more reasonable to listen and then judge than to shout out loud and be judged by the unreasonable.
Reasonable, perhaps. But realistic with 7.5 billion humans on this planet? And if other intelligences have evolved which are not hive minds, have they all managed to keep every citizen cosmically quiet as well? And if so by what measures? Draconian I would say.
As I read about each configuration, I would think “but what about…” and Dr. Benford would then address almost those exact questions.
Then we get to the plea for experiments:
I agree. However, Starshot is already a very small craft. How will a lab even get lasers and sail material to test components that will ultimately reach some fraction of the range of Starshot operating parameters? Are we going to need a facility like NIF at Livermore to test dime and marble-sized sails? That size of test would burn through Milner’s funding pretty quickly. What I would like to read about is what sort of tests Dr. Benford proposes, which can be done at Milner’s funding, and what the scope and funding would be needed before we could be confident that Starshot is viable and potentially worth continuing.
Starshot is rather different from most historic beamed sail proposals because it proposes very high beam intensities with short, but very high, acceleration. This is in contrast to the slower accelerations for long periods. It also requires new materials that are extremely reflective at the selected laser wavelength[s]. I would dearly like to see sails used for interplanetary missions, from probes like IKAROS to sample return to supply cargoes. Do interplanetary beamed sails need that sort of performance? To move larger payloads, those sails will dwarf any we have created to date. Starshot beam intensities and implied energies might be too expensive to contemplate for such sail fleets. Hopefully, Starshot experiments will indicate the sweet spots for such interplanetary sailcraft. I’d like to read more about how we get there from here.
Alex Tolley asks how we can demonstrate sail stability and high accelerations. As part of Star Shot, I’ve been looking into requirements of such facilities and have identified them fairly concretely. The necessary devices are a vertical experiment for stability and a horizontal experiment for high acceleration.
My basic concept for the vertical chamber is about 15 feet tall and would have a full complement of diagnostics to determine the stability of sails on beams, which could be microwave, millimeter wave, or lasers. At present time the cheapest approach is to use microwaves, and they are commonly available.
Once stability is understood, so that we know how to make a sail ride successfully on a beam, we move to demonstrate very high acceleration. That will require a rather long experimental chamber.
Recycling of photons to enhance acceleration, hence shortening the length of the ‘beam pipe’ for demonstrating high accelerations and velocities, is a downstream capability we must consider. The idea is to trap beam energy within the volume between the source and the sail. As the sail moves, it is the top cap to a “photon piston” that driving it. The Test Facility must have the capability to assess the amount of enhancement of acceleration that can be achieved in practice. No such experiment has been reported in the archival literature.
I’ve identified a site in the San Francisco Bay Area which could provide an appropriate facility. It’s located south of the Oakland airport in San Leandro. It covers about 3000 ft.². It would cost a few million dollars to build the necessary experiments.
I don’t understand how this cone can be stable. Once the craft tilts even a little, the beam pressure will be greater on that side and try to spin the spacecraft and sail. If you invert the cone, the dihedral will be self-correcting to keep it straight in the beam.
The payload at the end of the tether keeps the cone orientated correctly. This should be stable if the craft wanders off the beam center. Don’t think of it like aircraft dihedral wings to prevent roll.
Well, if you are looking at it as if the payload is providing ballast to stabilize the craft, then it seems more like a parachute, and will it will need many shroud lines to keep its shape, not just a central line.
Given the challenge of designing sails and payloads able to withstand such intense laser light at close proximity for high acceleration, perhaps some thought might be given to a first stage that uses intense radiation to create plasma, driving the craft up to a certain speed and distance, after which straight propulsion by light pressure would take over. Just a thought that might inspire others to do an assessment of the possibility.
The Benfords have shown that gas desorption from a carbon sail gives transient high thrust. This might be a useful way to get a sail quickly out of Earth’s gravity well.
I would like to see some experiments with beamed propulsion. A microwave beam that is received by a lightweight mesh antenna converted to electricity to run an ion or plasma engine. If the propellant could be a readily space-sourced volatile like water, then such high Isp engines could be both efficient and refuelable in space, saving on launch costs and allowing fleets to be built up.
Just as early steam ships also employed sails (and now oil powered ships are employing sails to add to the propulsion) I see no reason why such mixed propulsion system shouldn’t be used in space where the performance and economics warrants such use. High thrust engines are useful for rapid orbit changes, while photon sails are good for slow, low-cost propulsion.
We are at the early stages of exploring new propulsion technologies for deep space voyages. I suspect that a range of different approaches will eventually be used to economically and functionally match the task. One size may be dominant, but it probably won’t fit all.
I concur. One type of system might be a water-fueled, gridded ion thruster (or better yet, a Hall Effect thruster) array, with a microwave antenna receiver array (or a “laser-tuned” photovoltaic cell array) providing the electrical power for the thrusters and the other spacecraft systems. Its thrusters could even operate as a dual-mode propulsion system, which could work like this:
I was re-reading about the Space Coach (see: http://www.centauri-dreams.org/?s=Space+Coach ), which would use water-fueled electrothermal engines. Having also read up on the new, erosion-free external discharge Hall Effect thrusters (see: http://en.wikipedia.org/wiki/Hall-effect_thruster , http://arc.aiaa.org/doi/abs/10.2514/6.2016-4951 , http://web.stanford.edu/group/pdl/Papers/2005/Gascon-IEPC-2005-196.pdf , and http://repository.exst.jaxa.jp/dspace/bitstream/a-is/549895/1/SA6000036090.pdf ), an idea occurred to me:
Particularly for manned vehicles, using a high-ISP/low-thrust electrical thruster system (gridded ion thrusters and/or Hall Effect thrusters) would result in inconveniently-long (up to 1-1/2 years, as with ESA’s SMART-1 Hall Effect thruster-propelled lunar probe) “spiraling orbit to Earth escape” trajectories, although once free of the Earth and in solar orbit, such propulsion systems enable fairly fast trips to other planets.
Electrothermal thrusters (arcjets and resistojets), which produce greater thrust, would enable fast Earth escape trajectories and fast interplanetary transits, but at a price—a considerably larger fuel load, because electrothermal thrusters have significantly lower ISPs than ion and Hall Effect thrusters. I think a hybrid of the electrothermal thruster and the Hall Effect thruster is possible, and it might work as follows:
An external discharge Hall Effect thruster could be configured so that its annular “channel” was in the shape—as viewed in cross-section—of an annular expansion chamber and nozzle (if one cut such an engine in half from front to rear, it would look like it had two expansion chambers, each having a convergent/divergent nozzle). When operated in electrothermal mode, it would function just like any other electrothermal rocket engine, with its electrically-heated propellant expanding in the (annular) chamber and rushing out through the (annular) nozzle; this mode could be used relatively briefly, for the escape from Earth (and for braking into orbit around any massive body), and:
The electrothermal mode’s exhaust would be hot enough—especially if it were an arcjet type of electrothermal engine—to be ionized. (Either carbon electrodes, or perhaps refractory metal electrodes, could be used in the thrusters’ “combustion chambers” to produce the electrical arcs.
As an alternative, resistojets using white-hot tantalum resistors could be utilized instead or arcjets.)
This ionized mass flow could be electromagnetically accelerated to even higher exhaust velocities by engaging the Hall Effect thruster mode. (This dual-mode engine’s ISP could be varied by operating the electrothermal section at high, medium, or low thrust settings; during most of an interplanetary cruise [or an interstellar departure acceleration run], the fuel consumption could be kept very low [as with regular ion and Hall Effect thrusters] by running the electrothermal section at minimum thrust, and letting the Hall Effect section accelerate this low-mass-flow-per-second exhaust to the great speeds that are typical of Hall Effect thrusters.) Plus:
In fact, this dual-mode engine—because of its very mode of operation—might even exceed the ISP levels that are typical of regular Hall Effect thrusters; their ISPs, while high, are usually somewhat lower than the ISPs achieved by gridded ion thrusters. (A dual-mode electrothermal/gridded ion engine would also be possible, but it would be more mechanically complicated, because its grids would have to be folded or retracted out of the way of the nozzle, at least when its electrothermal mode was operated at high thrust—a dual-mode electrothermal/Hall Effect thruster, having no grids, could have no moving parts at all [except for its propellant valve, which would also serve as its throttle].)
A long way to go, in every sense of the word…
consider the maple seed… auto-rotating, and self stabilizing…
I don’t have the technical data, but its worth looking into.
also, speaking of a light weight material… I read somewhere that spider silk is supposed to be proportionately stronger than steel and and able to absorb in excess of 100,000 joules of kinetic energy (possible use in blast protection)… not sure it could take the heat from lasers though… but it also brings to mind the “sailing” that young spiders do… they let loose a silk thread into the wind which then transports them great distances.
The biggest problem I see for these high acceleration sail models above, is that stability achieved by them is global, not local. By which I mean the beam is actually pushing different areas of the sail in different directions, and stability requires transmitting substantial forces across the width of the sail.
At the accelerations proposed, VERY high forces relative to the mass of the material.
And yet, the sail is also expected to be at a relatively high temperature under the intense beam. Need I point out that this runs somewhat contrary to the demand that the sail be capable of carrying very high forces? Most materials weaken substantially at elevated temperatures.
Perhaps we should be aiming for local stability; Could a meta-material be designed which would reflect the beam in slightly different directions in response to stress, causing the reaction force to negate the stress, and thus remain stable in the beam without the transmission of high forces?
Wide beams with intensity above megawatt per square meter will heat up the air in their path and induce convection, inducing noise and strongly limiting collimation (maybe to tens of arcseconds for the proposed beam parameters)
I wonder if stability of the charged particle / magsail systems has been reinvestigated in the Breakthrough Starshot works. For any serious starshot, the propulsion unit must go into space; particle/magsail has much better energy efficiency and tunable Isp, but the stability is even more complicated than for lightsail…
‘I wonder if stability of the charged particle / magsail systems has been reinvestigated in the Breakthrough Starshot works.’
I don’t think that is in the scope of the project, but once I thought of using a laser tuned to the ionised gases particles in our upper atmosphere which would be shot off to hit a magsail and accelerate it.
Forgot the image,
https://malagabay.files.wordpress.com/2013/04/international-quiet-solar-year-daytime-ionospheric-and-atmospheric-composition1.gif
We may be better off using another company’s lab with aligned material requirements, after all this reflective material will be very useful for other projects such as orbital pumping and direction changes.
The closer this project dovetails with the communication industry the better and the lower the costs will be.
Excellent article. I don’t see any of the considerations cited as being showstoppers for StarShot, but some of them in combination come awfully close. There’s clearly, as DJ Kaplan says, “a long way to go”.
I’m afraid that if METI transmissions must wait for international consensus, we’ll all be waiting a long, long time before any such “official messages from Earth” are sent.
Even the late Scottish astronomy, astronautics (particularly interstellar space flight), and SETI/METI author John W. Macvey, for whom a possible interstellar invasion was not merely an academic concern, was not opposed to METI transmissions that are sent without international consensus regarding their content. (His 1979 book “Space Weapons/Space War” addresses the many ways that hostile–or desperate, or even indifferent [to humanity]–extrasolar visitors could take the Earth as their own and exterminate or subjugate the human race. I don’t recommend reading it while alone late at night under a starry sky, for the same reason that medical students find books about pathogenic microbes–and what they can do to us before we’re aware of it–troubling to read at such hours of the night.)
In his 1974 book “Whispers From Space” (which covers all aspects of SETI and METI, including Bracewell interstellar messenger probes and possible relay probes that could operate in support of them), Macvey expressed support–in principle–for consensus-approved METI transmissions, but he opined that as a practical matter, the difficulties involved in reaching such consensus would greatly delay such a METI program and would likely reduce the messages’ content to the lowest common denominator. He was able to point to an actual example of this:
At the 1971 international conference on CETI (Communication with Extra-Terrestrial Intelligence; this old, original “generic” term nicely includes all aspects of “listening” and “talking” to extraterrestrials, including via Bracewell probes, and even–if it ever occurs–face-to-face contacts) at the Byurakan Astrophysical Observatory in Soviet Armenia, it was decided that any interstellar transmissions should be carried out by representatives of humanity as a whole. When Frank Drake’s team acted unilaterally and sent the famous Arecibo message in 1974, after preparing it in apparent secrecy, this created a measure of ill feeling within the world scientific community. But as Macvey pointed out regarding this breach of CETI protocol:
“The whole affair sounds suspiciously like a storm in a tea-cup. The crux of the matter would seem to be that at least the thing got done–and apparently with the minimum of fuss and argument. On paper the deliberations and conclusions of august international bodies are all very well. In practice there is all too often a great deal of talk but little commensurate action–and when the action does eventually take place it is only after a great deal of wrangling and delay.” Also:
Since METI regulations are unenforceable anyway, and because many METI transmissions are made for cultural and even money-making reasons (like the star-naming companies–but at least the for-a-fee or by-subscription METI transmissions aren’t fraudulent, as the “officially-recorded” star names are…), the only realistic solution is to develop a list of voluntary principles for such interstellar transmissions. For example:
For scientific-oriented METI messages, the information included on the Pioneer plaques and the Voyager Interstellar Records could serve as “content templates” for the transmissions. For public participation METI messages, a short list of suggestions might suffice. They could include a (gentle) admonishment to participants to keep in mind that the signals will be like anything they post on the internet, and to consider what about themselves they would–and would not–want to be known not only by humanity, but by any number of other civilizations; such reminders would hopefully encourage humbler and more thoughtful “Hellos” to the universe.
Heck, no media bias here – not. Their views are obvious right from the title of this new NYT article on METI, not to mention the graphic farther down the piece showing a radio telescope that had just sent a message being destroyed by an alien laser beam:
https://www.nytimes.com/2017/06/28/magazine/greetings-et-please-dont-murder-us.html
I think we have far more to fear from members of our own human species than any hypothetical aliens.
In 2010 I wrote a two-part piece in this blog giving my reasons why I think we have little to worry about from ETI, or that if they do want our demise, they can do so with relative ease and we will be as unable to prevent it as we can prevent an earthquake or hurricane. And again, seven years later, not only do I still stand by my views but if anything the threat from other humans has only become greater.
Part 1 here:
https://centauri-dreams.org/?p=14703
Part 2 here:
https://centauri-dreams.org/?p=14754
Besides, as our technological civilization just gets electronically noisier, the less we will even be able to conduct radio SETI on Earth. So much for passive listening:
https://www.wired.com/story/your-connected-devices-are-screwing-up-astronomy
It may be easier to go straight to lasers as the communication industry increasingly uses them and they are getting cheaper. It would also make sense to build a small variable array so we can check the shapes of arrays to see which is better. Photon recycling would reduce the power consumption and scale of laser significantly. But I am not sure about how the reflections would affect the beam quality as they will create constructive/destructive interference.
Retroflective surfaces could offer a good way to control the forces getting out of control as they always point back to the source. They are also no more massive than a planar reflective surface but could suffer from absorbance if not polarised.
https://i.ytimg.com/vi/WRGfYqqjXDo/maxresdefault.jpg
Andrew Palfreyman
The issues in Star Shot are daunting and we’re going to attack the showstoppers in order of importance. A fairly complete list of the “challenges” appears here:
http://www.breakthroughinitiatives.org/Challenges/3
J Jason Wentworth
indeed it will take some time for agreement to be reached on whether to transmit and, if so, what to transmit. However it’s premature to transmit now. That’s because we simply don’t know where to transmit to. However in a decade or two, our increasing study of exoplanets with better and better space telescopes will likely reveal a planet in a habitable zone with biosignatures in its atmosphere. Then will have a possible target and eventually several targets.
Then we can be serious about it. I doubt that it would be within reach of any transmitters we presently have. It turns out that the scaling of cost-optimized interstellar transmitters is such that the power required goes only directly with the distance to that star. We can use the cost-optimized scaling to figure out how much it’s going to cost to build a really useful beacon.
Although some messages (besides the Arecibo one) have been transmitted by Western radio telescopes, this–particularly the public participation transmissions–seems to be an Eastern European phenomenon. Since the electricity bill (and the time spent in formulating and compiling the messages) is “on their dime,” I can’t object to it. Even if anyone out there is unlikely to be able to decode the messages due to their distance (although they might be able to detect the signals as RF noise at unusual frequencies for natural radio emissions), such projects may be useful as “practice efforts.”
But serious messages will require “serious output power,” and as you said, there are so many potential targets (at our current state of ignorance) that we’ll have to narrow down the list to likely abodes of intelligent life. Otherwise, the amount of power that would be required to repeatedly “beam” all of the (currently) potential stars (or Heaven forbid, to broadcast from an *omnidirectional* beacon that’s sufficiently powerful to send decode-able signals out far enough) might rival that required by the StarShot laser array.
The USSR/Russia has always been more into SETI than the West, although their recent reaction to that supposed signal from a star 95 light years distant calls their current feelings on the subject into question.
And now China has the largest single-dish radio telescope on Earth. They have officially and publicly expressed their desire to become the first nation to perform a successful SETI. Contrast this with Western astronomers who often put the subject way down on the list, if they mention it at all. The exception are Earth-like exoplanets, but that’s always a safe bet – or at least it has been since 1995. :^)
If China wants to do METI with FAST as well, who is going to stop them? While I too would prefer to see scientifically-inclined and “dignified” messages sent into the wider galaxy, not only does it seem like a futile effort to restrain and control every human with a transmitter but a violation of certain civil rights as well. They will simply end up having more of a negative effect on humanity than any imaginary aliens.
First European inflatable space sail deployment hailed a success – and it was made in Surrey:
http://www.getsurrey.co.uk/news/surrey-news/first-european-inflatable-space-sail-13332239
It was made for combating debris in LEO, but I am sure there are lessons to be learned for lightsails and such.