Looking around on the Net for background information about Jordin Kare, who died last week at age 60 (see yesterday’s post), I realized how little is available on his SailBeam concept, described yesterday. SailBeam accelerates myriads of micro-sails and turns them into a plasma when they reach a departing starship, giving it the propulsion to reach one-tenth of lightspeed. Think of it as a cross between the ‘pellet propulsion’ ideas of Cliff Singer and the MagOrion concept explored by Dana Andrews.
So I thought this morning to offer you some thoughts about SailBeam and its genesis from the man himself. I interviewed Jordin back in early 2003 in a wide-ranging discussion that took in most aspects of his work. He was an easy interview — all I had to do was offer the occasional nudge and he would take off. I found him engaging and hugely likeable. What follows is a fraction of the entire interview, the part that focuses primarily on SailBeam and a bit on Kare himself. I’ve edited it but in general preferred to let Kare’s own voice come through. The images I use here are from Jordin’s “SailBeam Space Propulsion by Macroscopic Sail-type Projectiles,” a presentation he delivered at the 2001 NIAC workshop in Atlanta.
PG: Your work with NIAC on the SailBeam concept takes sail technologies down a new path. Tell me how SailBeam and the NIAC report came about.

JK: I am an astrophysicist by background. I worked at UC-Berkeley and got a doctorate there in 1984. For most of the time since, I’ve been an aerospace engineer, dividing my identity between physicist and engineer. A lot of what I’ve worked on in this area are advanced propulsion projects. So I’ve been involved in a community of people who do exotic propulsion things.
One of the things that’s always in my mind is doing advanced interstellar propulsion. In this case, I’d been aware of ideas for doing laser and microwave sails for interstellar propulsion. Bob Forward did prototypical work on that. I’d been involved in couple of workshops where he talked about the concept, one at the Jet Propulsion Laboratory a couple of years back.
Along those lines, I had realized that there’s a scaling law to how laser sails worked. If you took a laser sail and tried to get to a certain velocity with a certain size laser and certain size sail, and then you took that sail and cut it into several pieces and accelerated those one after another, you could get the same amount of mass to the same velocity in the same amount of time, but you could use a smaller laser because the sail doesn’t accelerate over as long a distance.
That was interesting but not very useful. And then I thought about work that Geoffrey Landis had done about using sails not made of metal foils. The trouble with small sails is that you’re pushing them harder, accelerating faster. And if you’re using metal sails, you can’t do much of that before they just melt. Landis had pointed out you could push harder on dielectric sails.
——-
PG insert: A brief bit of background on this. The problem with metal films is that they have low emissivity. A small sail made of such materials overheats under the beam. High emissivity materials with higher melting temperatures are needed. Dielectrics are non-conductive materials that will emit a lot but absorb little of the radiation impinging upon them. Silicon carbide is a dielectric, as is aluminum trioxide and, Kare’s favorite, diamond. But back to the interview.
——-
JK: Dielectric sails that are a thin layer of transparent material reflect better than metal foil sails because they have a different index of refraction [describing how light propagates through a particular medium], like the reflection off the surface of a piece of glass, or reflection off a metal film. Forward noted that dielectric sails could potentially have higher acceleration.
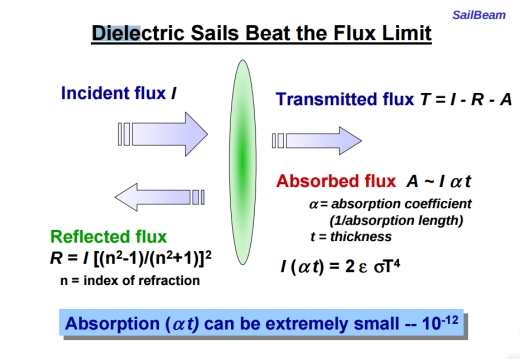
My mental light bulb went on and said I know from working in laser technology and other areas I work on, that you can make very low absorption dielectric materials. If I can make very high quality, very low absorption dielectrics, I could push them really hard. Now instead of thinking in terms of taking a sail and dividing it into ten pieces, I can divide it into a million pieces. I started doing calculations and realized that this made sense as a propulsion system.
I started pulling in pieces from other projects I’ve worked on. This got to the point where I could make a rough design of the system concept and started telling my associates about it. I did a quick presentation at a meeting of space people that we exotic propulsion people go to — the Space Technology and Applications International Forum every January in Albuquerque.
I was describing the SailBeam idea to Bob Forward and he was the one who said you should get some money out of NIAC to study this further; he’d been involved with reviewing stuff for NIAC. I knew other people who had worked with them, so I went to the next NIAC workshop and did a proposal for the following round. When I looked at the kinds of things NIAC was supporting, SailBeam fit with the tenor of their proposals.
PG: Of course the whole idea of sail technologies is changing.
JK: It is for sure, and we have to distinguish between solar and laser sails, or beamed energy sails. The idea of solar sails has been around for a long time. And there have been many changes of direction. They used to look primarily at metallic sails for solar sail missions, usually metallic sails coated on a plastic film. But people who were really aggressive thought in terms of free-standing metal sails. Just in the last couple or three years, carbon-carbon has emerged. Here we have carbon fibers fused together to make an open lattice material that is as lightweight as anything they were ever hoping for out of metal-coated plastics, and much easier to handle. Carbon-carbon also takes much higher temperatures than plastic film.
Suddenly the solar sail people began looking at Sundiver missions, where they fly a solar sail and let it drop close to the Sun, flying edge on until it gets well inside the orbit of Mercury and then turning it face-on to the Sun for that propulsive kick. This gives you much higher velocities than anything we’ve done today, something like 100 or 200 kilometers per second, which means this has application for missions far past Pluto. This kind of velocity lets you begin to talk about thousand astronomical unit missions, a true interstellar precursor.
PG: Missions to another star demand even more. A lot more.
JK: True. Bob Forward was working at Hughes on some of the earliest lasers back in the 1960s when he first came up with the beamed sail idea. His idea was that if you have a laser or microwave beam, you can focus much more energy over a longer distance than you can with sunlight. You can use the same light pressure that solar sail people are talking about to get much higher velocities. Forward came up with this thing called Starwisp [a microwave-driven wire-mesh sail about a kilometer in diameter with a flight time of 20 years to Alpha Centauri — see The Case for Beamed Sails].
Forward realized there were problems with the basic Starwisp concept. One that always bothered me was how Bob was going to get any useful information out of this Starwisp. He talked about having little sensors at the intersections of this fine wire mesh, magically having them turn into a large telescope aperture. I was never quite clear how that actually worked.
So that was his first notion of a very high velocity sail. Forward also came up with concepts for laser sails, in particular the multistage laser sail that would be able to decelerate at destination by splitting off part of the sail and using that to reflect the beam back onto a separate section. A lot of people were interested in that and the idea got used in a lot of science fiction, including Bob’s own writing.
I’ll mention there’s a paper Bob Forward wrote for a workshop I ran at Livermore in 1986, when we were looking at non-interstellar laser propulsion applications. His paper was “Laser Weapon Target Practice with GeeWhiz Targets.’ And in there he talked about a sail that was made of multiple layers of diamond film. I had almost forgotten about this when I came up with my notion of the SailBeam. He had the idea of using dielectric reflectors by way of getting to extremely high performance in a sail.
I use artificial diamond as the best material for my sail. So Bob, as was usually the case, had some of the same pieces considerably earlier than anyone else. But he also had much thicker sails with more layers and wasn’t trying for quite such high performance. He was talk about building something that could fly at perhaps 100 kilometers per second using the types of laser we were talking about building for strategic defense.
The problem with his interstellar propulsion scheme, and everyone agreed it was a problem, was the scale that was required. Because Bob Forward wrote about 10,000 kilometer diameter Fresnel zone plate lenses. He would show an artist’s conception of the lens hanging next to the Earth, and it was the same size as the Earth! The sail by itself would be a hundred or thousand kilometers in diameter, and the lasers were in the terawatt category. It was clear that in principle it would work, but it was, to say the least, a monumental engineering task.
We all wondered if we could do this better somehow. At a workshop out at the Jet Propulsion Laboratory, Geoff Landis ran the session on laser sails and we looked at how you could make smaller sails, asking what was the smallest sail you could build and still do interesting missions. We were still looking at a single laser pushing a single sail.
It was hard to come up with something buildable and still interesting, but Landis had looked at optimizing sails in terms of choosing the best possible material. He was the one who pointed out there was this notion of designing not with multiple layers of dielectric that Bob Forward had put into his ‘gee whiz targets’ paper, but with a single layer of dielectric a quarter wavelength thick. That plus the scaling property that I had been thinking about were some of the ingredients that led to the SailBeam.
PG: SailBeam works by turning your micro-sails into plasma to push the departing spacecraft.
JK: This is where Dana Andrews’ work with magsails was so critical. The notion of putting magnetic coils on a spacecraft, essentially a magnetic loop, and making a magnetic field around it to deflect the solar wind, the stream of charged particles from the Sun. I had done some work for Dana on MagOrion, a notion of making the magnetic field strong enough that you could set off an atomic blast behind the spacecraft and deflect the plasma produced by the bomb.

PG: This was the Project Orion idea applied to magsails.
JK: Exactly. The magsail replaces what would have been a physical sail. The idea was designed originally for cruising around inside the Solar System. But magsails and all these other threads tie together — remember that the original invention of the magsail came when Dana Andrews and Bob Zubrin were trying to figure out if they could make the Bussard ramjet work. They wanted to see what you could do if you were trying to collect interstellar hydrogen with a magnetic scoop. And what they discovered is that they couldn’t make a Bussard ramjet work, because the magnetic fields always ended up deflecting the ionized hydrogen at high velocity. What that turns into is a very good drag brake.
Tweaking the numbers a bit, they could make it be a drag break against the solar wind, which is flying along at a pretty good velocity in the Solar System, 75 K per sec or so. So they could fly around on the solar wind. But all this originated from looking at another interstellar propulsion concept. These ideas build on each other; they’re hybrids.
So I had been working on MagOrion, had done designs of the field coils for Dana Andrews, and that was another piece, because I wondered if I can accelerate little bitty sails and do this scaling of launching a million little sails instead of one big sail, what do I do with them? They are too small to be useful individually. Well, I can use them like a MagOrion. I can turn them into blobs of ions and bounce them off a magnetic field at the vehicle. So I got to pull in yet another piece from things that other people had come up with that I adapted for my own design.
PG: You also applied magsail to deceleration in the target stellar system.
JK: Exactly. One of the things that Dana and Bob Zubrin had pointed out in the past is that a magsail worked as a way of decelerating interstellar spacecraft. I’m carrying a magsail anyway, so Dana and I collaborated on an IAF paper on slowing down a SailBeam vehicle at the far end. Now we had both a way of accelerating and reusing some of that hardware to stop at the far end.
PG: This seems like a more realistic way to do it than Forward’s ‘staged sail’ concept.
JK: I think it is. The one limit on it is that it is not a very fast braking system. It does take tens of years to stop. And it doesn’t bring you down to a full stop. That’s because the force you get to slow down varies with how fast you’re going. So the slower you’re going, the less you slow down. At some point, the time it takes to slow down from a tenth of the speed of light to one percent of the speed of light isn’t too bad, but it takes progressively longer to slow down the rest of the way. You can argue design details as to whether you can get down slow enough that you can then come to a stop by braking against the wind from whatever star you’re approaching. That gives you an extra 75 or 100 kilometers per second for the wind velocity to work against.
Or maybe you’re going to have to carry some system like nuclear electric to slow you down the last 100 kilometers per second. Forward’s sail in principle would let you come to a complete stop or reach any final velocity you wanted to. But it does seem like a very difficult thing to do. It’s in the category of ideal technology. It’s pretty hard to see how you’d actually build it.
PG: You talk about using relay lenses along the acceleration path for your micro-sails. How does this system improve the original design?
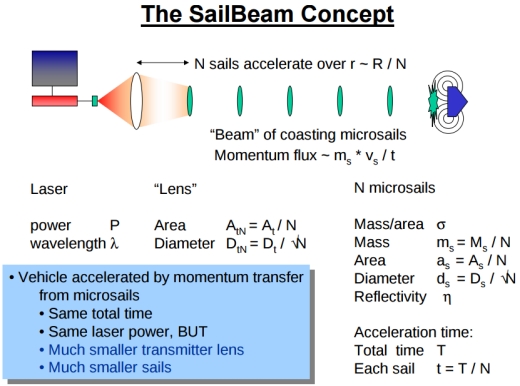
That was something i realized late in the process of doing the design. My little sails accelerate over short distances by comparison to Forward’s big sail concepts, a few tens of thousands of kilometers. The problem with pushing a big sail is that I have this one big lens that has to focus the light on the sail some large distance away. How about if I take a smaller lens and use it to focus light, but then I put another lens at a place where the beam spreads out again. And I put another lens out and focus the beam yet again. So I have this spaced series of lenses.
It’s pretty easy to show this is not a useful thing to do if you’re trying to accelerate a large sail over a light year. Partly because you have to put the intermediate lenses a large fraction of a lightyear away and partly because you don’t gain when the lens and the sail are about the same size. There’s no advantage to it; you end up having the same amount of material in multiple lenses as you would in one big lens. Geoff Landis did a paper to show why it doesn’t work.
With my situation, though, I was only accelerating things for a few tens of thousands of kilometers. I had been thinking I’ll do this with one big telescope, a 500 meter telescope. But at some point I realized I’m taking this 500 meter telescope and focusing the beam on this little tiny sail. If I were to try to focus on another lens, another telescope, i could do that easily. I’m only accelerating over a short distance, so I can physically put a telescope forty thousand kilometers away; it’s not like I have to put it half a light year away.
So I realized I could build a 50 meter telescope and have 10 of them. Because of the way the numbers work out, because I’m focusing on a very small object, it turns out I gain in terms of the total area of the telescopes. I can make ten telescopes each a tenth of the diameter and spaced one tenth of the way along the path. And end up using, since each telescope is a tenth of the diameter, a hundredth of the area. So I can have ten times the total material of the telescopes.
Now I had gotten the lens down from 10,000 kilometers to a few hundred meters. Which certainly helps. Look, Bob Forward figured out a way you could get to the stars using known physics. Cliff Singer talked about using particle accelerators for ‘pellet’ propulsion. Both these notions left us huge engineering problems. What Geoff Landis and I both did was to say, can we do better from an engineering standpoint. Can we make this something we can actually build.
What I like best about Sailbeam is that as far as I know right now, it is the most engineering-practical way to get up to a tenth of speed of light.
PG: These sails get up to speed, shall we say, quickly.
JK: Yes. In some of the designs they go from zero to light speed in about a tenth of a second. That’s pushing it and in the design that’s in the final proposal, they take about three seconds. I love showing that slide — it shows what the limiting acceleration would be for an ideal microsail and it’s like 30 million gravities, or zero to lightspeed in .97 seconds. But even backing up because of materials properties, you’re talking about accelerating at hundreds of thousands of gravities and getting up to a large fraction of lightspeed in a few seconds.

PG: And you’re pushing, in an ideal scenario, an interstellar probe of what size.
JK: The baseline is a one ton probe. There really is nothing, you probably can’t go a lot smaller than that, though i wouldn’t swear you couldn’t build a one kilogram probe. But even with sophisticated miniaturization, it becomes hard to make a useful probe that’s much smaller than a ton. So I tend to look at that size scale. On other hand, there isn’t an upper limit. You could build much bigger probes, but they would cost more to build the lasers to launch them. The laser power you need is proportional to the mass.
PG: Up to near lightspeed in a second! You seem to be somebody who enjoys pushing the boundaries.
JK: It’s definitely a lot of fun to do. The interesting part of my work is coming up with new schemes and combinations to see if they work. The flip side is that interstellar flight is such a hard problem that you don’t get the satisfaction of something you expect to see built.
PG: Interstellar flight is all about long time frames. Even mission durations of 50 to 100 years are wildly beyond our current capabilities. So how do you cope with this perspective — long-term thinking isn’t something our culture has much patience with.
JK: It’s certainly something that is pretty rare in our society. Although I am occasionally amazed because on the one hand people don’t think long term, and then, on the other hand, I see people worrying about things like Social Security going bankrupt in thirty years. We have no idea of what the economy is going to be like in thirty years. So there are a few places in our society where people do think long term, but most of them don’t seem to me to be. Actually this is an interesting phenomenon.
PG: The notion of working on projects where you won’t get results in a lifetime or more is rare indeed. But from talking to you, I get the idea that you would be pleased to think that something you did today would contribute to a mission that might not launch until you and I are both gone.
JK: That’s absolutely true. I would be delighted if when I am old and gray, I discover that people are just starting to work on building something like SailBeam and are referring to me as having come up with the idea, or part of the idea. It’s not that I can’t imagine this SailBeam concept actually being launched within my lifetime — it’s not impossible — but it’s as much as I can reasonably expect to hope that in my time on Earth we’ll maybe be getting started on it.
PG: You’re also a science fiction fan.
JK: Yes. No fiction of my own rather than the occasional song. But I do often point out that I write both science fiction and fantasy. It’s just that the science fiction is usually titled ‘technical proposal’ and the fantasy is titled ‘budget proposal.’ I have never turned pro like Geoff Landis.
Certainly I’ve been an SF reader since way back when. I will note in fact that if there was any single book that turned me onto the notion of engineering interstellar flight, it would be the book Tau Zero by Poul Anderson. That was the one that got me going, stimulating a lot of interest in interstellar flight as something that we might actually make happen.
——-
Jordin’s report on SailBeam concepts is “High-Acceleration Micro-Scale Laser Sails for Interstellar Propulsion,” Final Report, NIAC Research Grant #07600-070, revised February 15, 2002 and available here. And see Geoffrey Landis’ “Optics and Materials Considerations for a Laser-propelled Lightsail,” presented at the 40th International Astronautical Federation Congress, Málaga, Spain, Oct. 7-12, 1989 (full text).



given the “lack of long-term thinking in our society”, and judging from current discussion (cf. Loeb et al.; talk begins @ 13:00) @
http://youtube.com/watch?v=72e3Bx0EgiA
Breakthrough Starshot – despite the $100 million from Milner – isn’t going to work out as currently envisaged:
1) @ 20% lightspeed the timeframe (c. 24 years) to get to Proxima and receive (very little) information is way too long. Emperor Haxo IV will cancel the project for sure. That’s if not forgotten altogether while underway. Got to be faster. Maybe .8 lightspeed and then work out
2) some kind of past-halfway there braking system so that the instruments don’t flash by the target at relativistic speeds, but instead go into orbit around target and transmit lots of information over a matter of weeks, months or longer. One way to brake might be to launch the sails in pairs, with the first of each pair (via reverse firing lasers) acting as a brake for the instrument-bearing trailer.
I disagree strongly with that. The Voyager probes are now ~40 years on, and they will likely be returning data for about another 10 years. A total of 50 years. We haven’t turned off the Deep Space Network, we regularly listen to the Voyagers returning data from the outer portions of the heliosphere and now the interstellar medium. I fail to see why a mere 24-30 years is at all unrealistic for a robotic interstellar mission. Even 50 years is not totally unreasonable (especially if you give the job of receiving data to multiple entities to ensure long-term viability).
And 0.8c is absurdly hard. Even if you solved propulsion, it presents nearly insurmountable transit hazards. I’m much more of a fan of 0.1c as JK suggested.
point taken. But Voyager didn’t take 24 years to START returning data. And then produce only a few seconds worth. $100 million, even for a billionaire, isn’t pocket change. At this rate of return, astrophysics is going to run out of billionaires fast. Of course, if we could liquidate the warfare/welfare state, there’d be plenty of money for space.
“A society grows great when old men plant trees whose shade they know they shall never sit in.” -Greek Proverb
There are pitfalls on the path of individual and collective life, short-term, medium-term, long-term and even very-long term. Only with a perspective that covers them all can a person or a community avoid them all.
Depending on the barrel length, maneuverability and defense capability, that would make a pretty decent weapon, a potential satellite killer. Good for targets in a vacuum, yet probably useless for targets on Earth as the sails are too insubstantial and would instantly vaporize in the atmosphere. (Of course, using the laser directly would make it useful for targets on Earth.)
How does a series of lenses maintain the beam, yet still accelerate the sails without them hitting the lenses?
I don’t know the answer to that one, Alex. But Sandy Montgomery at MSFC has worked on multiple lens deployment for beaming, if memory serves, and I hope to get the chance to ask him the question at the next TVIW.
One approach would be for the sails and probes to thread a hole down the center of the lenses, and just refocus the light that diverged enough to miss the hole. They are, after all, much smaller than the lenses, and have to be traveling with great precision anyway to stay in the beam for such a long distance.
‘How does a series of lenses maintain the beam, yet still accelerate the sails without them hitting the lenses?’
The lens have a hole in them so the diverging laser light (off the sail gets directed back on to the sail, that is the way I see it.
So the image with the single lens to show the concept is misleading when applied to multiple lenses? An annular lens allowing the sail to pass through it would lose a lot of the energy unless the beam was also annular. I can see (I think) that such an arrangement would have any individual beam make a zig-zag path as it is redirected through the lenses.
The cost of this approach is that the sail would not be intercepting the beams all the time. This might be a tradeoff worth making, I don’t know.
Interestingly silicon has very good properties for a sail material, it can also take huge laser pulses, thousands to millions of what ‘Starshot’ would use. That is why I think 60 000 g forces will be very conservative indeed, we may indeed go into millions of ‘g’s shortening the acceleration distance considerably. This concept can be tweaked a bit to deliver a system that can push payloads happily around the solar system and to the stars.
https://www.osapublishing.org/DirectPDFAccess/F77B8C2F-9D3D-7876-0455E9E57794646C_244873/oe-20-S6-A984.pdf?da=1&id=244873&seq=0&mobile=no
Wont the small sail beam have to move though the exhaust from the probe? Will that cause problems with the sails moving at a fraction of the speed of light? Is this issue addressed at all?
I haven’t seen that addressed, Jim, though Jordin may have covered it in one of his presentations. Let me see what I can find about interactions at the departing spacecraft.
I think the long-term-thinking issue will stop being such a big issue very soon. I think aging will be basically cured in less than 50 years.
Didn’t Asimov write a short story where an interstellar ship project was never launching a ship because the researchers had been given immortality, and so felt no urgency? They just kept refining the plans instead of building the ship.
Has anyone bought up the amount of signal jamming thats going to come from Proxima Centauri as the probe swings in system to look at Proxima B? 2000x electromagnetic radiation once you are on top of Proxima B is going to kill even the most hardened circuits. You likely need a baseball diamond three dee printed around it.
A one ton probe? How about a carry-all and a bunch of microsats?
For me, the first problem I think of is how a signal would be transmitted back to terra firma from that vast distance in a form that we can detect and use.
Is “spooky action at a distance” going to solve this?
https://www.space.com/37506-quantum-teleportation-record-shattered.html
And can we cram whatever required circuitry onto a postage stamp chip?
Jason Davis
October 27, 2017
Here’s how engineers closed out LightSail 2 for flight
Last month, engineers reconfigured The Planetary Society’s LightSail 2 spacecraft into its flight-ready state for what is likely to be the last time. It’s a big milestone for the program; after years of effort dating back to 2009, work on the CubeSat is finally finished.
The procedure to button up LightSail is called closeout. The team sets the spacecraft’s software to start the mission on the next boot, and physically secures all deployable structures including the antenna and solar panels.
LightSail 2 spent 2017 in a hurry-up-and-wait mode while launch dates remained fuzzy for SpaceX’s Falcon Heavy rocket. The uncertainty provided an opportunity to perform more tests and tweaks, with the knowledge that the order to ship the spacecraft could come at any time.
Launch is currently scheduled for no earlier than April 30, 2018. But that could always change, based on the timing of one or possibly two Falcon Heavy flights ahead of the STP-2 mission for the U.S. Air Force, which will carry LightSail 2 and its partner spacecraft, Prox-1, as secondary payloads.
Full details and lots of detailed technical images of the satellite here:
http://www.planetary.org/blogs/jason-davis/2017/20171020-ls2-closeout.html