One reason we look so often at sail technologies in these pages is that they offer us ways of leaving the propellant behind. But even as we enter the early days of solar sail experimentation in space, we look toward ways of improving them by somehow getting around their need for solar photons. Robert Zubrin’s work with Dana Andrews has helped us see how so-called magnetic sails (magsails) could be used to decelerate a craft as it moved into a destination system. Now Zubrin looks at moving beyond both this and solar wind-deflecting electric sails toward an ingenious propellantless solution. Zubrin presented the work at last April’s Breakthrough Discuss meeting, and today he fills us in on its principles and advantages. Read on for a look at a form of enhanced electric sail the author has christened the Dipole Drive.
by Robert Zubrin

Abstract
The dipole drive is a new propulsion system which uses ambient space plasma as propellant, thereby avoiding the need to carry any of its own. The dipole drive remedies two shortcomings of the classic electric sail in that it can generate thrust within planetary magnetospheres and it can generate thrust in any direction in interplanetary space. In contrast to the single positively charged screen employed by the electric sail, the dipole drive is constructed from two parallel screens, one charged positive, the other negative, creating an electric field between them with no significant field outside. Ambient solar wind protons entering the dipole drive field from the negative screen side are reflected out, with the angle of incidence equaling the angle of reflection, thereby providing lift if the screen is placed at an angle to the plasma wind. If the screen is perpendicular to the solar wind, only drag is generated but the amount is double that of electric sail of the same area. To accelerate within a magnetosphere, the positive screen is positioned forward in the direction of orbital motion. Ions entering are then propelled from the positive to the negative screen and then out beyond, while electrons are reflected. There are thus two exhausts, but because the protons are much more massive than the electrons, the thrust of the ion current is more than 42 times greater than the opposing electron thrust, providing net thrust. To deorbit, the negative screen is positioned forward, turning the screen into an ion reflector. The dipole drive can achieve more than 6 mN/kWe in interplanetary space and better than 20 mN/kWe in Earth, Venus, Mars, or Jupiter orbit. In contrast to the electric sail, the ultimate velocity of the dipole drive is not limited by the speed of the solar wind. It therefore offers potential as a means of achieving ultra-high velocities necessary for interstellar flight.
Background
The performance of rockets as propulsion systems is greatly limited by their need to carry onboard propellant, which adds to the mass which must be propelled exponentially as the extent of propulsive maneuvers is increased. For this reason, engineers have long been interested in propulsion systems that require no propellant.
The best known propellantless system is the solar sail, which derives its thrust by reflecting light emitted by the Sun. Solar sails are limited in their performance however, by their dependence upon sunlight, which decreases in strength with the square of the distance, and the laws of reflection, which dictate that the direction of thrust can only lie within 90 degrees of the vector of sunlight. Moreover, because photons move so swiftly, the amount of thrust that can be derived by reflecting light is at best 0.0067 mN/kW (at 100% reflectance, full normal incidence), which means that very large sails, which necessarily must have significant mass and be difficult to deploy, must be used to generate appreciable thrust. As a result, while solar sails have been studied since the time of Tsiolokovsky [1], we are only now beginning to experiment with them in space.
An alternative to the solar sail is the magnetic sail, or magsail, which was first proposed by Zubrin and Andrews in 1988, and subsequently analyzed extensively by them in a variety of further papers [2,3] in the 1990s. The magnetic sail uses a loop of superconducting wire to generate a magnetosphere to deflect the solar wind. Assuming the development of high temperature superconducting wire with the same current density as existing low temperature superconductors, a magsail should be able to generate significantly higher thrust to weight than is possible with solar sails. However such wire has yet to be developed.
Another propellantless propulsion system of interest is the electric sail [4], which like the magsail operates by deflecting the solar wind, in its case by using an electrostatic charge. As a result, like the magsail, the classic electric sail (electric sail) cannot operate inside of a planetary magnetosphere other than as a drag device, has its thrust decrease with distance from the Sun, and is limited in the potential direction of its thrust. Because of the low momentum density of the solar wind, electric sails must be even bigger than solar sails. However, because only sparsely spaced thin wires are needed to create sail area, higher thrust to mass ratios can be achieved than are possible using solar sails which require solid sheets of aluminized plastic.
Electrodynamic tethers [5] have also been proposed, which use the interaction of a current in a tether with the Earth’s geomagnetic field to produce thrust. In addition to facing a variety of engineering and operational issues, however, such systems can only operate in a planetary magnetic field and can only thrust in a direction normal to the field lines, a consideration which limits their applicability.
Finally, we note recent claims for a system called the EM Drive [6], which according to its proponents can generate about 1 mN/kWe, in any direction, without the use of propellant, an external light source or plasma wind, or magnetic field. Such performance would be of considerable interest. However, as it appears to contradict the laws of physics, there is reason to suspect that the measurements supporting it may be erroneous.
As a result, there clearly remains a need for a new type of propellantless propulsion system, which can operate both inside and outside of a planetary magnetosphere, can thrust in a multitude of directions, and which is not dependent upon sunlight or the solar wind as a momentum source. The dipole drive is such a system.
The Dipole Drive
The principle of operation of the dipole drive while accelerating a spacecraft within a planetary magnetosphere is illustrated in Fig. 1 below.
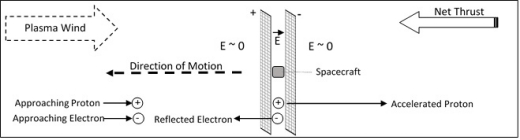
Fig. 1. The Dipole Drive Accelerating within a Magnetosphere.
In Fig. 1 we see two parallel screens, with the one on the left charged positive and the one on the right charged negative. There is thus an electric field between them, and effectively no field outside of them, as on the outside the field of each screen negates the other. There is also a voltage drop between the two, which for purposes of this example we will take to be 64 volts.
Protons entering the field region from the left are accelerated towards the right and then outward through the right-hand screen, after which they escape the field and experience no further force. Protons entering from the right are reflected towards the right, adding their momentum to that generated by the protons accelerated from left to right. There is thus a net proton current from left to right, and a net proton thrust towards the left.
In the case of electrons, the situation is exactly the opposite, with a net electron current from right to left, and a net electron thrust towards the right. Note that while electrons entering from the right will be greatly accelerated by the field, reflected electrons will only be reflected with their initial velocity. There will also be an electron current through the outside plasma to neutralize the net proton flow to the right.
Because space plasmas are electrically neutral, the number density of both electrons and ions (which for the moment we will consider to be protons, but may which – advantageously – be heavier species, as we shall discuss later) will be the same, so the proton and electron electrical currents will be equal, as will the power associated with each of them. However because the mass of a proton is about 1842 times as great as the mass of an electron, the thrust of the proton current will be about 43 times greater than the opposing electron current thrust (because the momentum of particles of equal energy will scale as the square root of their mass, sqrt(1842)=43) and the system will generate a net thrust. The acceleration of the electrons is a form of drag, which is provided for by loss of spacecraft kinetic energy. It therefore could, in principle be used to generate electric power, partially compensating for the power consumed to accelerate the protons. In the following examples, however, we will assume that there is no provision for doing this, i.e. that the efficiency of any such energy recovery is zero.
To see what the performance of a dipole drive might be, let us work an example, assuming a 500 W power source to drive the system. The electron current negates about 2% of the thrust (1/43rd) produced by the proton current. The maximum possible jet power is thus about 490 Wj. Assuming additional inefficiencies, we will round this down to 400 Wj, for a total system electrical to jet power efficiency of 0.8.
A Coulomb of protons has a mass of 0.011 milligrams. If the jet power is 400 W, and the potential difference is 64 V, so the proton current will be 6.25 A, and have a mass flow of 0.0652 mg/s.
The relationship of jet power (P) to mass flow (m) and exhaust velocity (c) is given by:
P = mc2/2 (1)
Taking P = 400 W and m = 0.0652 mg/s, we find that c= 110,780 m/s. Since thrust (T) is given by T=mc, we find:
T = mc = 7.2 mN (2)
This is a rather striking result. It will be recalled that the electrical power driving this system is 500 W. So what we are seeing here is thrust to power ratio of 14.4 mN/kWe, more than ten times better than that claimed for the EM Drive, but done entirely within the known laws of physics!
If it is desired to deorbit (decelerate) a spacecraft, the direction of the screens would be reversed, with the negative screen leading in the direction of orbital motion. In this case, the screens would become a proton reflector. An electric sail could also be used as a drag device to serve the same purpose. However, because the dipole drive doesn’t merely create drag against passing protons, but reflects them, it would create twice the drag of an electric sail of the same area. If the dipole drive is positioned obliquely to the wind angle, it can reflect protons, with the angle of incidence equaling the angle of reflection. For example, if it is tilted 45 degrees to the wind, a force will be generated perpendicular to the wind, that is “lift” will be created. Such maneuvers could also be done with the dipole drive in acceleration mode, deflecting protons to combine lift with thrust. Using this capability, a dipole drive propelled spacecraft in orbit around a planet could execute inclination changes.
To summarize, in contrast to the electric sail which can only create drag against the wind to lower its orbit, the dipole drive can thrust in any direction, raising or lowering its orbit or changing its orbital inclination. In addition, when used as a drag device, the dipole drive can create twice the drag per unit area as the electric sail.
The Dipole Drive in Planetary Orbit
Let us therefore analyze the system further. The dipole drive exerts no field outside of its screens, so the only plasma it collects is the result of its own motion through the surrounding medium. So how big does its screen need to be?
We consider first the case of the above described dipole drive system operating in LEO at an altitude of 400 km, being used to thrust in the direction of orbital motion. It is moving forward at an orbital velocity of 7760 m/s. The average density of ions at this altitude is about 1,000,000 per cc. Assuming (conservatively) that all the ions are protons, the required ion mass flow of 0.0652 mg/s would be swept up by a screen with a radius of 127 m.
It may be noted however, that at 400 km altitude there are also O+ ions, each with a mass 16 times that of a proton, with a numerical density of about 100,000/cc. These therefore more than double the ion mass density provided by the protons alone. If these are taken into account, the required scoop radius would drop to about 80 m.
Another way to reduce the scoop size would be by going to higher voltage, so that more power can be delivered to a smaller number of ions. If, for example, we quadrupled the voltage to 256 volts, the exhaust velocity would double, to 222 km/s, allowing us to cut the mass flow by a factor of four, and the scoop radius by a factor of two, to just 40 m. The thrust, however, would be cut in half, giving us 3.6 mN/kWe.
As we go up in altitude, the plasma density decreases, as does the orbital velocity, requiring us to go to larger scoops. Examples of 500 W dipole drive systems operating at a variety of altitudes are provided in Table 1. In Table 1, Vo and C are orbital velocity and exhaust velocity, in km/s.
Table 1. Dipole Drive Systems Operating in Earth Orbit (Power=500 W)
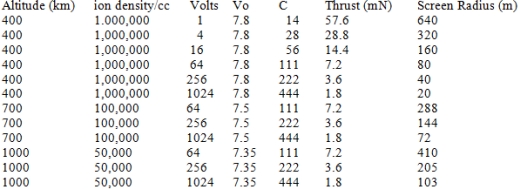
It can be seen that the dipole drive is a very attractive system for maneuvering around from LEO to MEO orbits, as the high ion density makes the required scoop size quite modest. It should be emphasized that the above numbers are for a 500 W system. If a 5 W dipole drive thruster were employed by a microsatellite, the required scoop areas would be reduced by a factor of 100, and the radius by a factor of 10.
It may be noted that Mars, Venus and Jupiter all have ion densities in low orbit comparable to those above. For example, Mars has 500,000/cc at 300 km, Venus has 300,000/cc at 150 km, and Jupiter has 100,000/cc at 200 km, making the dipole drive attractive for use around such planets as well. Many of the moons of the outer planets also have ionospheres, and the dipole drive should work very well in such environments.
As one ascends to higher orbits, the density of ions decreases dramatically, while the orbital speed decreases as well. For example, in GEO, the ion density is only about 20/cc, while the orbital velocity is 3 km/s. These two factors combine to make much larger scoops necessary. So, for example, in GEO, a 500 W dipole drive operating at 1024 volts would need a scoop 3.6 km in radius.
Because the effectiveness of the dipole drive decreases at higher altitudes while operating within the magnetosphere, the best way for a dipole drive propelled spacecraft to escape the Earth is not to continually thrust, as this would cause it to spiral out to trans GEO regions where it would become ineffective. Rather, what should be done is to only employ it on thrust arcs of perhaps 30 degrees around its perigee, delivering a series of perigee kicks that would raise its apogee on the other side of its orbit higher and higher until it escaped the magnetosphere and became able to access the solar wind.
The Dipole Drive in Interplanetary Space
The dipole drive can also operate in interplanetary space. Compared to planetary orbit, the ion densities are lower, but this is partially compensated for by much higher spacecraft velocities relative to the plasma wind. As a result, the required scoop sizes are increased compared to planetary orbital applications, but not by as much as considerations of ion density alone might imply.
Let us consider the case of a dipole drive traveling in heliocentric space at 1 AU, positioned at an angle of 45 degrees to the wind, with its negative screen on the sunward side. It would thus reflect solar wind protons 90 degrees, thereby accelerating itself forward in the direction of orbital motion. A diagram showing the dipole drive operating as a sail in interplanetary space is shown in Fig. 2.
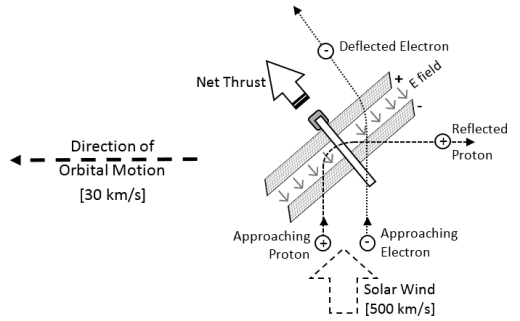
Fig. 2 The Dipole Drive Operating as a Sail in Interplanetary Space.
The solar wind has a velocity of 500 km/s, so to insure reflection, we employ a voltage of 2028 volts, sufficient to reverse the motion of a proton moving as fast as 630 km/s. With a density of 6 million protons per cubic meter, the wind has a dynamic pressure of 1.25 nN/m2. As the sail is positioned 45 degrees obliquely to the wind, its effective area will be reduced by a factor of 0.707, with the thrust reduced to 0.9 nN/m2. In this case, virtually all of the protons hitting the sail will be coming from the sunward side, and since they are reflected without adding any kinetic energy, no power is required to drive them. However, we still have an electron current coming from the sunward side being accelerated outward. This requires power. With 500 W, total radial thrust would be 1.27 mN, with 1.27 mN also delivered in the direction of orbital motion, for a L/D ratio of 1. The total effective screen area would therefore need to be 1,414,000 m2, with an actual area of 2,000,000 m2, requiring a radius of 798 m. Total thrust to power would be 3.6 mN/kWe.
If instead we had not concerned ourselves with obtaining complete deflection of each particle, we could have used a lower voltage. This would increase the thrust per unit power, but increase the required sail area for a given amount of thrust. So, for example, if we chose 512 volts, we would have a total thrust of 3.6 mN, for a thrust/power ratio of 7.2mN/kWe, but need a sail radius of 1127 m.
It may be noted that all of these results are for a 500 W dipole drive. A microsatellite might employ a 5 W dipole drive, in which case the required scoop radii would drop by a factor of 10.
The thrust and diameter of a 1 kWe dipole drive system operating as a solar wind sail in interplanetary space at 1 AU is shown in fig. 3.
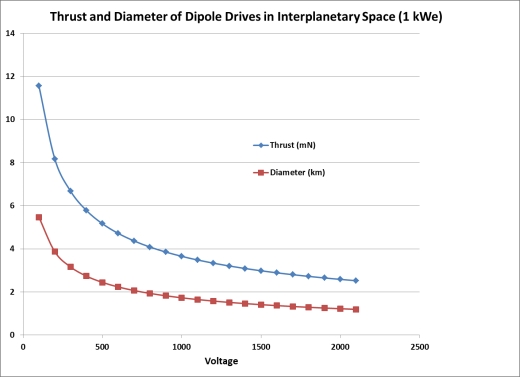
Fig. 3. Thrust and Diameter of a 1 kWe dipole drive system operating as a solar wind sail in interplanetary space.
Use of the Dipole Drive for Interstellar Flight
In contrast to the electric sail, the dipole drive can be used to accelerate a spacecraft at velocities greater than that of the solar wind. For example, consider a spacecraft moving away from the Sun at a velocity of 1000 km/s. The solar wind is following it at a velocity of 500 km/s, so relative to the spacecraft there is a wind moving inward towards the sun at a velocity of 500 km/s. In this case, to accelerate the spacecraft would direct its positive screen away from the sun. This would cause it to accelerate protons sunward, while reflecting electrons outward, for a net outward thrust. At 500 km/s the protons are approaching the spacecraft with a kinetic energy equal to 1300 volts. It can be shown that employing a screen voltage difference that is about triple the kinetic voltage produces an optimal design for an accelerating system, while one using a voltage difference equal to the kinetic voltage is optimal for deceleration. This is illustrated in figs 4 and 5 which respectively show the kinetic voltage as a function of velocity, and the relative power/ thrust and area/thrust ratios of the spacecraft as a function of the dimensionless parameter Z, where Z=(engine voltage)/(kinetic voltage.)
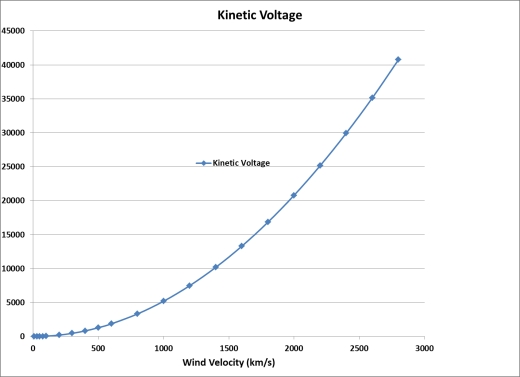
Fig 4. Kinetic Voltage as a function of spacecraft velocity.
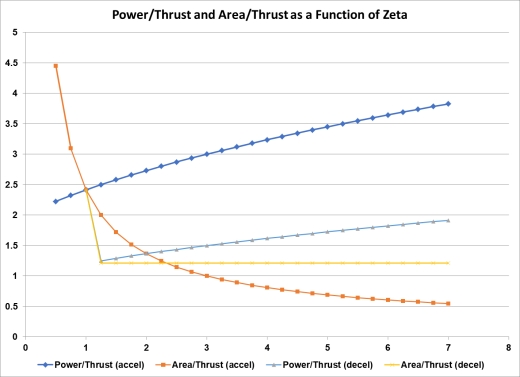
Fig 5. Relative Power/Thrust and Area/Thrust as a function of Z=(engine voltage)/(kinetic voltage.) There is a step factor of 2 increase in thrust during deceleration when Z reaches 1, because protons are reflected. For acceleration, Power/Thrust ~ 1 + sqrt(1+Z), while Area/Thrust ~ 1/(-1 + sqrt(1+Z)).
If we add 3900 volts to the incoming protons, quadrupling their energy, we will double their velocity relative to the spacecraft, thereby providing an effective exhaust velocity of 500 km/s. The solar wind has a density of 6 million protons/m3 at 1 AU, with ambient density decreasing to 1 million/m3 in interstellar space. If we take the former value, we get a thrust of (1.67e-27 kg/proton)(500,000m/s)2(6,000,000/m3) = 2.5 nN/m2. If we take the latter value, it would be 0.42 nN/m2. The proton current at the smaller value would be 80 nA/m2, which at 3900 volts works out to 0.312 mW/m2. The thrust to power ratio would therefore be 1.35 mN/kW. (This ratio would also hold true at the 1 AU value, but the magnitudes of both the thrust and power per unit area would be six times greater.)
If a dipole drive powered spacecraft were receding 500 km/s directly away from the Sun, it would see no relative wind and thus produce no thrust. However, like a modern sailboat that can sail faster crosswind than downwind, because it can generate lift, the dipole drive can get to speeds above 500 km/s by sailing across the wind. As the spacecraft’s crosswind speed increases, it becomes advisable to turn the sail to ever greater angles to the solar wind and increasingly normal to the crosswind. As this occurs, the L/D resulting from solar wind reflection increases while the total solar wind thrust decreases. At the same time, however, thrust resulting from the acceleration through the screens of crosswind protons increases, maintaining total thrust constant at ever higher L/D (relative to the solar wind) levels. Once the crosswind velocity exceeds the solar wind velocity the solar wind becomes increasingly irrelevant and the dipole drive becomes a pure acceleration system, driving the incoming crosswind plasma behind it to produce thrust,
As the speed of the spacecraft increases relative to the wind, it is necessary to increase the voltage in order maintain thrust/power ratio efficiency. For example, let’s say we want to achieve 3000 km/s, or 0.01c. Then the kinetic energy equivalent voltage of the approaching protons would be 47 kV. So, to double this velocity we need to quadruple the total voltage, or add a sail voltage drop of 141 kV. The proton current would have a value of 480 nA/m2, with a power of 68 mW/m2. The thrust would be 15.1 nN/m2, for a thrust to power ratio of 0.22 mN/kW.
It may be observed that since the necessary voltage increases as the square of the velocity, with power increasing with voltage but thrust increasing with velocity, the thrust to power ratio of the dipole drive decreases linearly with velocity. This puts limitations on the ultimate velocity achievable. For example, the most optimistic projections for advanced large space nuclear power systems project a mass to power ratio of 1 kg/kW. If we accept this number, then, neglecting the mass of any payload or the dipole drive system itself, then the system described in the previous paragraph performing with a thrust to power ratio of 0.22mN/kilowatt at 3000 km/s would have an acceleration of 0.00022m/s2, or 7 km/s per year. The average acceleration getting up to 3000 km/s would be twice this, so the spacecraft would take 214 years to reach this speed. During this time it would travel 1.07 light years. To reach 6000 km/s (0.02 c) starting from negligible velocity would require 857 years, during which time the spacecraft would travel 8.57 light years. The performance of such a system is shown in Table 2. Note 63,000 AU = 1 light year. The performance shown assumes an advanced 1 kg/kWe power supply. If a more near-term power system with a higher mass/power is assumed, the time to reach any given distance increases as the square root of the mass/power ratio. So for example, if we assume a conservative near-term space nuclear power reactor with a mass/power ratio of 25 kg/kW, the time required to reach any given distance would increase by a factor of 5.
Table 2. Advanced Dipole Drive Performance for Ultra High-Speed Missions (1 kg/kW power)
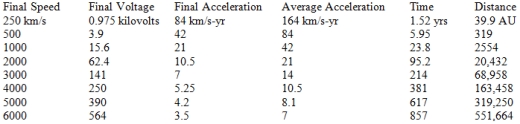
It can be seen that advanced dipole drive spacecraft could be quite promising as a method of propulsion for missions to near interstellar space, for example voyages to the Sun’s gravitational focus at 550 AU. Unless much lighter power systems can be devised than currently anticipated however, they would still require centuries to reach the nearest stars. Power beaming may provide an answer. However such technologies are outside the scope of this paper.
If a spacecraft has been accelerated to interstellar class velocities, whether by means of the dipole drive or any alternative technology, the dipole drive provides a means of deceleration without power (it could actually generate power) by creating drag against the relative plasma wind. This feat can also be done by a magnetic sail or an electric sail. However because it can also create lift as well as drag, the dipole drive offers much greater maneuverability during deceleration as well as a means to freely maneuver within the destination solar system after arrival.
Dipole Drive Design Issues
Let us consider the case of a 2 kg microsatellite operating in LEO, with 5 W of available power to drive a dipole drive. (Note, a typical CubeSat has a mass of 1.3 kg. At 20 kg/kWe, a 5 W solar array should have a mass of about 0.1 kg.) If we operate it with a voltage of 16 Volts, it will produce 28.8 mN/kWe, or 0.144 mN thrust over all. It would have an acceleration of 0.000072 m/s2. This would allow it to generate a ΔV of 2288 m/s in a year, sufficient to provide extensive station keeping propulsion, substantially change its inclination, or to raise it from a 400 km altitude orbit to a 700 km orbit in 1.6 months. To generate this much thrust at 400 km would require a scoop with a radius of 16 m, while doing so at 700 km would require a scoop with a radius of 58 m. Let us assume that the scoop is made of aluminum wire mesh, using wires 0.1 mm in diameter separated by distances of 2 m. Each square meter of mesh would thus have about 1 m length of wire. This needs to be doubled as there are two meshes, one positive and one negative. Therefore, a scoop with a radius of 16 m would have a mass of 32 grams. If the propulsion system were used simply for station keeping, inclination change, or deorbit functions at the 400 km altitude, that’s all that would be needed. To operate at 700 km, a 116 gram scoop would be required. From these examples we can see that the use of the dipole drive to provide propulsion for microsatellites in LEO could potentially be quite attractive, as the modest scoop sizes required do not pose major deployment challenges.
Now let us consider a 100 kg interplanetary spacecraft in interplanetary space, operating with 500 W at a voltage of 2028 volts. From the discussion above it can be seen that this would generate about 2.54 mN of thrust in the direction of orbital motion. The scoop would need to have a radius of about 800 m. In interplanetary space, the Debye shielding length is ~60 m, and so a screen with a 20 m mesh would suffice. Such a screen would have a mass of about 8.5 kg, which would be well within the spacecraft mass budget. The 2.54 mN thrust would accelerate the spacecraft at 0.000025 m/s2. It could thus impart a V to the spacecraft of about 804 m/s per year. Higher accelerations could be provided by increasing the spacecraft power to mass ratio.
The deployment of large scoops composed of two parallel, oppositely charged meshes poses operational and design issues. Prominent among these is the fact that the two opposite charged screens will attract each other. However the total force involved is not that large. For example, let us consider a configuration consisting to two sails of 500 m radius separated by 500 m with a 2 kV potential difference. Then the electric field between them will be 4 volts/m. The area of each screen will be 785,400 m2. From basic electrostatics we have EA = Q/ε, so Q, the charge of each screen will be given by Q=(4)(785,400)(8.85 e-12) = 0.000028 coulombs. The electrostatic force on each sail is given by F=QE, so the total electrostatic force of each sail will be 0.1 mN. This is about a tenth the thrust force exerted by the screens themselves. Nevertheless, as small as they are, both of these forces will need to be negated. This can be done either with structural supports or by rotating the spacecraft and using artificial gravity to hold the sails out perpendicular to the axis of rotation. An alternative is to use the self-repulsion of the charge of each sail to help hold it out flat. In such a configuration two sails held separate from each other by a boom attached to their centers could be expected to curve towards each other at their edges until the stiffening self-repulsive force on each sail from its own charge balanced the bending forces exerted by the spacecraft’s acceleration, the push of the wind, and the attractive force of the opposite sail.
One way to avoid such issues would be to design the system as a literal dipole, with a rod holding a positive charge at its end to the front of the spacecraft, and a rod holding the negative charge pointing to the rear of the spacecraft. Seen from a distance, such a configuration is electrically neutral and would exert negligible field. However, in the zone between the charges, there is a strong field from one pole to the other. Particles entering this field along the rod center lines would experience the full voltage drop. Particles entering the field at some distance from this central axis would experience a lower voltage drop. The overall functional voltage of such a system, from the point of view of power consumption and exhaust velocity, would be an average over many particles entering the dipole field at all distances from its axis. This is obviously a more complex configuration to analyze than that of the two parallel screens discussed so far, but it may be much simpler to implement in practice on an actual spacecraft.
A critical issue is the material to be used to create the dipole drive. In his original paper on the classic electric sail [4], Pekka Janhunen suggested using copper wires with diameters between 2.5 and 10 microns. This is not an optimal choice, as copper has a much lower strength to mass ratio than aluminum, and such thin strands would be quite delicate. For this reason, in the above examples we specified aluminum wire with 100-micron diameters. A potentially much better option, however, might be to use aluminized Spectra, as spectra has about 10 times the yield strength of aluminum, and roughly 1/3 the density (Aluminum 40,000 psi, 2700 kg/m3, compared to Spectra 400,000 psi, 970 kg/m3.). Spectra strands with 100-micron diameters and a coating of 1 micron of aluminum could thus be a far superior material for dipole drive system, and classic electric sails as well. An issue however is Spectra’s low melting point of 147 C. Kevlar, however, with a yield strength of 200,000 psi, a density of 1230 kg/m3, and a melting point of 500 C could provide a good compromise. Still another promising option might be aluminized strands made of high strength carbon fiber, such as the T1000G (924,000 psi, 1800 kg/m3) produced by Toray Carbon Fibers America.
Some options for dipole drive spacecraft configurations are show in in Fig. 6. As can be seen, small dipole drive systems can be used for spacecraft control, for example as an empennage. Such small dipole drive units could also be used for attitude control on non-dipole drive spacecraft, such as solar sails.
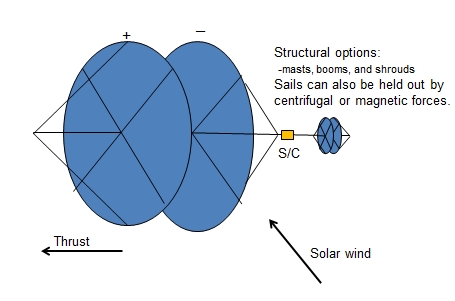
Fig. 6. Options for dipole drive spacecraft configuration. Small dipole drive systems can be used for attitude control.
As with the electric sail, the dipole drive must deal with the issue of sail charge neutralization caused by the attraction of ambient electrons to the sail’s positive screen. In reference 4, P. Janhunen showed that the total such current that an electric sail would need to dispose of would be modest, entailing small power requirements if ejected from the spacecraft by a high voltage electron gun. In the case of the dipole drive, the current would be still smaller because the spacecraft has no net charge. In addition electrons acquired by the positive screen could be disposed of by using the power source to transport them to the negative screen. Alternatively, if an electron gun were used, its required voltage would be less than that needed by an electric sail because external to the screens, the dipole drive’s field is much weaker and falls off much more quickly. For these reasons, the issue of sail charge neutralization on the dipole drive should be quite manageable.
Because the dipole drive does not interact with plasma outside of the zone between its screens, the issue of Debye shielding of its screen system to outside charges is not a concern. Debye shielding of its individual wires within screens can be dealt with by means of adequately tight wire spacing. As shown by Janhunen [4], such spacing may be quite liberal (~60 m in near Earth interplanetary space), enabling sails with very low mass to area ratios. [7]
Conclusion
The dipole drive is a promising new technological concept that offers unique advantages for space propulsion. Requiring no propellant, it can be used to thrust in any direction, and both accelerate and decelerate spacecraft operating within planetary magnetospheres, in interplanetary space, and interstellar space. Unlike magnetic sails and electric sails, it can generate both lift and drag, and its maximum velocity is not limited by the speed of the solar wind. Near-term dipole drives could be used to provide a reliable, low cost, low mass technology to enable propellantless movement of spacecraft from one orbit to another, to provide station keeping propulsion, or to deorbit satellites, as required. Then dipole drive could also be used as a method of capturing interplanetary spacecraft into orbit around destination planets, or of lowering the orbits of spacecraft captured into initial elliptical orbits using high thrust propulsion. The latter application is particularly interesting, because it could enable a small lightweight lunar ascent vehicle to carry astronauts home from the Moon by launching directly from the lunar surface to trans-Earth injection and then subsequently lower itself to LEO to rendezvous with a space station or reentry capsule spacecraft without further use of propellant. Such an approach could potentially reduce the mass of a manned lunar mission to within the launch capacity of a single Falcon Heavy. Because it needs no propellant, the dipole drive offers the unique advantage of being able to provide its propulsion service to any spacecraft indefinitely. While the dipole drive is most attractive in orbital space whether ambient plasma is thickest, it can be used in interplanetary space and even enable interstellar missions as well, becoming more attractive for such applications as ancillary technologies, such as power generation evolve.
There are many technical issues that need to be resolved before practical dipole drive spacecraft can become a reality. However both the theory of dipole drive operation and it potential benefits are clear. Work should therefore begin to advance it to flight status. The stars are worth the effort.
References
1. Jerome Wright (1992), Space Sailing, Gordon and Breach Science Publishers
2. D. G. Andrews and R. Zubrin, “Magnetic Sails and Interstellar Travel”, IAF-88-553, 1988
3. R. Zubrin and D.G Andrews, “Magnetic Sails and Interplanetary Travel,” AIAA-89-2441, AIAA/ASME Joint Propulsion Conference, Monterey, CA July 1989. Published in Journal of Spacecraft and Rockets, April 1991.
4. Pekka Janhunen, “Electric Sail for Spacecraft Propulsion,” J. Propulsion, Vol. 20, No. 4: Technical Notes, pp763-764. 2004.
5. Cosmo, M.L., and Lorenzini, E.C., Tethers in Space Handbook, NASA Marshall Space Flight Center, 1997
6. D. Hambling, “The Impossible EM Drive is Heading to Space,” Popular Mechanics, September 2, 2016.
7. “Debye Length,” Plasma Universe.com, https://www.plasma-universe.com/Debye_length accessed Feb 18, 2018.



Dr. Zubrin,
It’s a fascinating concept but I’d like to see a comparison toDr. Young Bae’s laser thruster concept for solar system travel.
https://www.nextbigfuture.com/2017/02/yk-bae-can-now-amplify-photonic-laser.html
Also, regarding your statement that the EMDrive, there are a range of reported results up hundreds and even around 1000 mN/KW for the Cannea results. The 1 mN/KW number is not the complete data set so far and further, is not from optimal engineered drives but low power test systems.
There is big difference between EMdrive and Dipole drive – EMdrive seams to be based on some new principles, and have to be tested and researched in the labs. When Dipole drive claimed (by author) to be based on the known physic , but in reality has nothing common with physical laws. The basic concept of Dipole drive supposes , that protons in electrical field (in described by author situation and system) will create greater thrust than electron – is absolute false.
Probably , there will be some electrical current between electrodes in this dipole, but no any thrust is possible in neutral media (plasma) the forces from positive and negative charged particles will be equal, and the particle mass difference plays no role in this fact. After charged particles acceleration in dipole electrical field summary forces and energy balance will stay ZERO…
I might be mistaken, but isn’t this basically the same kind of propulsion as with an ion drive. But the dipole drive use no Xenon fuel, instead propels with plasma from the surrounding space.
So it could work, but like one Ion drive, it will need to insert electrons together with the Ion so the craft don’t get electrical charge. And the ‘exhaust’ dont perhaps even fold back on the craft and cancel the trust.
Real life Ion drive takes care about electrons :-)
Dipole drive concept supposes (falsely) that :
if you will apply electrical potential to system composed by two electrodes (anode and cathode) that located in ionized media , the external drug force (thrust) will be applied to this system and this force has negative to positive electrodes direction.
Other words the pressure on this system from the negative electrode side will be higher than from positive electrode…
Now, I just read an article on the true power of the solar wind.
http://www.spacedaily.com/reports/The_true_power_of_the_solar_wind_999.html
“The solar wind consists of charged particles – mainly hydrogen and helium ions, but heavier atoms up to iron also play a role,” explains Prof. Friedrich Aumayr from the Institute of Applied Physics at TU Wien.
“These particles hit the surface rocks at a speed of 400 to 800 km per second and the impact can eject numerous other atoms.”
“Up to now it was assumed that the kinetic energy of the fast particles is primarily responsible for atomization of the rock surface,”
When the particles of the solar wind are multiply charged, i.e. when they lack several electrons, they carry a large amount of energy which is released in a flash on impact. “If this is not taken into account, the effects of the solar wind on various rocks are misjudged,” says Paul Szabo.
Perhaps this can all be taken into account for the design, with a dual solar wind/lightsail design:
https://www.newscientist.com/article/mg22630235-400-spacecraft-built-from-graphene-could-run-on-nothing-but-sunlight/
“Its flat structure is very strong and conducts electricity and heat extremely well….a Graphene sponge could be used to make a light-powered propulsion system for spacecraft that would beat solar sails.”
Tsander’s self-eating sail?
The discussed dipole drive is not targeted to effectively use solar winds energy… The described dipole grids – cannot effectively interact with solar winds particles…
“The basic concept of Dipole drive supposes , that protons in electrical field (in described by author situation and system) will create greater thrust than electron – is absolute false.”
You’re assuming the plasma between the grids is neutral, because the plasma entering the front is neutral. But that’s not true: Protons being much more massive, they have a much longer residence time inside the grid than the electrons.
So you have a net positive plasma exposed to the inter-grid voltage. Thus a net force.
Another way of looking at it is that both protons and electrons are given the same increment of *energy* if they pass through the grid.
But energy is 1/2mv2, while momentum is mv. So a given amount of energy produces more momentum for heavier particles. Again, net production of momentum.
***
I can see other potential problems, though. If you’re reflecting protons at the front of the grid, and accelerating electrons out the back, the local plasma in front of the grid will be net positive charge, and behind net negative. Wouldn’t this tend to negate the dipole field of the grid itself?
@Bertt Bellomre
Your quote:
“Protons being much more massive, they have a much longer residence time inside the grid than the electrons.”
You make some big mistakes, in your argumentation,
1. because do not take in account that charged particles in cosmic vacuum have their own energy and it has order of Mega/Giga/ etc. electronVolts, so additional 64eV or even 1000eV, that will not change significantly travel time of charged paticles between electrodes.
2. On other sight particles that have higher speed will enter and leave closed volume much faster, so will fill “empty” space, wich demon can stop electrons to enter between grids? Is there some physical law?
3. Do you suppose that positively charged volume will attract electrons and repell protons? Or space between the dipole grids has it’s own physical laws?
4. If someone ,once , can accept this your argument he should automatically postulate that every closed volume of (neutral ) cosmic plasma will be positively charged, because protons too lazy to move :-) You do not need to have electrodes, to implement your dream, lazy will sit on the place and sfift will leav it fast, so according your argumentation – the neutral plasma is impossible…
“You make some big mistakes, in your argumentation,
1. because do not take in account that charged particles in cosmic vacuum have their own energy and it has order of Mega/Giga/ etc. electronVolts, so additional 64eV or even 1000eV, that will not change significantly travel time of charged paticles between electrodes.”
That’s not a mistake. At least, it’s not a mistake on my part. The mass/energy of the particles is irrelevant if we’re not doing anything that alters their fundamental character, just altering trajectories. All we’re concerned about is kinetic energy in the reference frame of the sail.
Typical solar wind energies are on the order of 1-2 thousand electron volts. A grid charged up to a potential difference of three or four thousand volts, easily managed, would have no trouble reflecting almost all protons under normal circumstances. Coronal mass ejections would be quite another matter, and cosmic rays would be essentially uneffected. But, of course, cosmic rays are largely irrelevant to this discussion anyway, as they are mostly isotropic in direction, and so this sort of sail couldn’t derive any thrust from them anyway.
So, real numbers: A 4kv grid with an inter-grid spacing of 1m. Solar wind speed of 400 kps.
Your proton has about 840 ev, it only penetrates 21 cm into the inter-grid space, and then heads right back out. Rough estimate, it spends about half a microsecond in the inter-grid space.
Your electron, traveling at the same speed, has about half an ev of energy. Ends up with, of course, 4kev, about 3.7^7 m/2. So it spends, roughly, a twentieth of a microsecond in the inter-grid space.
So, on average, there are going to be ten times as many protons as electrons in the inter-grid space.
Now, there are a lot of assumptions here. I’m assuming that the solar wind is thin enough that space charge considerations are negligible, for instance. Really a full simulation is called for, there are a lot of factors that could degrade the performance of this sort of sail, like protons piling up in front of it.
But the basic concept is sound, I can see that even though I took my last electrodynamics course in the 70’s.
@Brett Bellmore
I got (from internet ;-)) different energy order for charged particles energy in interspace vacuum.
But in reality it is not so important to our discussion.
The particle kinetic energy can be used only in the case when you have full energy exchange between the dipole and particle (i.e. particle absorbed or reflected from the grid) . To get the dipole acceleration you should apply some external force on it. And described dipole cannot create this force in neutral media (in reality it cannot create thrust in charged media too), because forces from negative and positive charged particles will be equal for the equal charge. Particles in vacuum moving in any direction so for described drive even full reflection (absorption) of charged particles summary will create zero force (moment) too, till you will build specially sail to make deal with solar winds.
Described device is not propulsion device, so particle momentum is not transferred to the dipole directly, there is only electromagnetic interaction between the dipole and charged particle and interaction is limited by electromagnetic forces only. So when we are talking about “thrust” from passing through electrodes particles (it is main thrust source of described drive) initial momentum of particle, direction, speed , mass of particle are not important – the only things that we should take in account electromagnetic forces that are depends only on charge…
If there is a net positive charge between the grids, this will tend to reduce the potential difference (and hence the E field) across most of the grid separation. This reduces the distance over which an acceleration of ions would occur. So the very thing (net positive charge) that would be increasing the efficiency of the drive will simultaneously tend to nullify the supposed drive effect. These are all qualitative assessments. To really know, a practical model should be developed and placed in orbit to test the concept. As with the Em Drive, care in setting up the experimental apparatus is critical to establish valid empirical results.
The positive and / or negative charge beween the grid can exist – for short time intervals, but average will be zero.
The positive (and oppiste – negative) charge between the grids will repel protons and attarct electrons (and opposite) , so that will automatically recover neutral media state.
It cost nothing to check Zubrin’s electrical DC current calculations between grids :-)
This current is key element in expected thrust calculations, if those numbers are multiple orders lower than described in article – there is no reason to continue any test nor in lab nor in space…
> Proven but classified technology should enable photonic propulsion to operate out to 100 kilometers.
But the distances in consideration here are far larger. Phased arrays of lasers might be able to extend the distance, so there is an off chance you can power it using them.. That said, easier said than done, and think perhaps the potential effective aperture is better seen as best upper case.
EMDrive is BS.
This concept claims to be “real physic”, but in basic source , it have no connection to wishful thinking…
There is lot of fault I have found in this idea, but basic one is enough to eliminate whole idea…
Despite proton mass is more than 3 order higher than electron’s mass, proton and electron will always get exactly same energy amount (and as seauence same impulse) from the same electric field – it is the basic law of electrostatic… So in the neitral media that contans the same amount of negative and positive charged particles it will not produce any thrust…
There is additional discrepancy in the article, but this one fact is more than enough…
Sorry , but EMdrive or Mach drive are much more scientific based than this “idea”.
XDDDDD So a drive that contradicts well stablished physical principles is more real than one based on well stablished physical principles XDDDDDD
Sorry, but proposed Dipole drive contradict all modern physical principles, take this article and to any good high school physics teacher he can explain why this idea has no scientific ground.
All of them contradict well established physical principles, but the Dipole Drive is a trivial oversight compared with the elaborate contortions used to justify the others.
The proton and electron get the same *energy* from the voltage difference, but a different *momentum*. E=p_p²/2m_p = p_e²/2m_e
so p_p/p_e = sqrt(m_e/m_p)
Also the EMdrive is BS.
If it works, and several smart people think it might, it would be far more useful that the Dipole Drive. Just declaring it’s ‘BS’ doesn’t add anything. Besides, even if the EMDrive doesn’t pan out, that doesn’t mean the MACH effect thruster won’t. And, there are other EM based propellent-less drive concepts being worked on.
EM conserves momentum.. If it works, it involves something else than EM.(or it has propellant) But these devices are well inside known physics, EMdrive claims it is not outside know physics. It’s exceedingly unlikely.
There are theories such as McCulloch’s quantized inertia and other ideas to explain it.
How you will apply (transfer) this momentum to the dipole drive?
To accelerate the drive you should apply some external force or “loose” some mass with some speed (propulsion)…
We know that external forces are zero (energy balance is zero), and there is no any mass losses (propulsion) in this drive…
Charged particles are not part of the dipole drive – it is only free “visitors” from the vacuum…
There’s no specific example worked out. To assess whether such a spacecraft makes sense we need a clear description of the spacecraft’s embodiment: what is its mass, size, energy source for maintaining the potential, etc.?
I also wonder whether the ambient medium that the spacecraft is to be in, such as a planetary magnetosphere, would allow electrons coming in from the side to short out the potential. To assess that we would have to know what the local electric field is but, although the voltages are specified, the electric field is not because the gap has not been given. I’d like to know whether or not there’s any possibility that electrons coming in from the sides could short out this potential.
Energy that will get (give) charget particle in electric field is calculated by very simple equation:
W = C*U,
where :
C – is electrical charge
U – electrical potential difference (in this case voltage) between electrodes
So both proton and electron will get the exactly same energy from the proposed Dipole thruster, as sequence in electrically neutral media – there will be same thrust from electrons and protons (or ions), i.e. no thrust from this device, useless.
Now before I comment to what you have just written above, I have to stress that I only made a quick scan of what was being said in the article above, and so this is more reflexive and off-the-cuff, then a detailed rebuttal to what you have just stated.
But haven’t you made the assumption within your argument above that there exist an EQUAL number of positive and negative ions entering into the gap that exists between the two potential surfaces? Unless I’m mistaken, the article did not make a statement that at any particular instance, there existed an equal number of negative and positive charges existing that would diffuse into the gap. Admittedly, the author did state that OVERALL the ion species that exist in outer space is a type of neutral soup, but he did not specifically state that ions (positive and negative) diffuse into the electrified gap in equal numbers.
Or am I missing something?
Charley,
You make simple things more complicated that it is in reality :-)
Author wtires about neutral medai (plasma), this means that summary volume charge is ZERO, i.e. summary charge of positive and negative charged particles is equal.
Equal charges (positive and negative) will create the equal force i.e. equal energy collected (spreaded) in both directions, the difference in charged particles masses plays no role in this situation.
Authors makes huges mistake supposing that more massive positive charged particles will give higher force and as sequence thrust – modern physic deny this, author should invent the new electristatic laws the get this things work…
You should return to high-school physics class XD. Kinetic energy is 1/2 mv^2 and momemtum is mv. Equal energy doesn’t produce equal momentum for different masses.
“Authors makes huges mistake”
http://www.alternativephysics.org/comedy/img/facepalm.jpg
@Antonio,
I see that I’ve found persone who can help me to undersnd better high-scool physic, so I have some questions to you:
1. Can you explain please , how the particle momentum will be transferred to the dipole energy (momentum) , which physical law you will apply to this transfer?
2. What kinetic energy (momentum) do have charged particles in interstellar cosmic vacuum? (I mean most probable, expected value, order)
3. What is ration between initial energy (momentum) of charged particle and energy (momentum) that it will collect (dissipate) between the dipole’s grid (use numbers from Zubrin’s concept).
4. What will be electric field strenght near external (outside) surface of the grid on the ditance that is equal to 1/2 of the ditance beween the dipole’s electrodes.
5. How is formed DC current between electrodes.
etc., etc.,
@AlexT:
1. Coulomb’s law.
2. It depends on the particle. Galactic cosmic rays vary hugely in kinetic energy and mass.
3. It’s already detailed in the article.
4. Negligible. The exact value depends on the size of the sail and the calculation is complex, but nevertheless it’s easy to see that it’s negligible for the sizes and voltages considered using Gauss law and some cutting here and there.
5. There are losses of charge from particles colliding with the wires and from electrons escaping from the wires attracted by flying protons.
@Antonio,
Thanks, so:
1. Ok, Coulomb’s law tell us that electrostatic force between charged body depends on charge only… Electron and proton will interact with dipole with the same force, two equal force that have opposite direction will give summary zero force (acceleration).
2. In reality particle energy is not important in this concept, this question is for reference to a people that suppose protons and electrons are stay without any motion in vacuum waiting only the dipole drive grid voltage to get some movement :-)
3. Sorry , but article has multiple mistakes and speculations exactly in this area, and it is not high-school :-) For example article supposes that higher momentum of proton will bring to the dipole acceleration, with energy balance zero, without mass losses – acceleration … fun.
4. I cannot accept your minds on this issue, sorry. If you will look well in this comment you will find there link to scientific work dedicated to calculation of external electromagnetic field of parallel capacitor, it is not so negligible if distance from charged body to surface comparable with the distance between capacitor’s plates.
5. I suppose that passing by proton, does not have enough energy to cause escape of electron from the wire :-) But quantum mechanic gives some probability to this case too.
So , if you somehow understand this point, please explain me, how Dr, Zubrin can get next numbers in his calculations (quote following below):
” If the jet power is 400 W, and the potential difference is 64 V, so the proton current will be 6.25 A”
Do you suppose that all charged particle will “fall” onto electrodes?
To get 6.25A of direct current between grids with voltage 64VDC, in interstellar vacuum – very optimistic numbers even for vacuum tube with directly heated cathode…
Sorry, I meant that there in this topic, one of commenters gave the link to related article.
Yes, but you’re not quite getting it right. The energy a proton receives from the dipole is equal to the energy an electron receives, but the momentum is not. For example, if we take the proton as weighing 1600 times the electron (a crude approximation), then the speed added to the proton is 1/40 of the speed added to the electron. But since the proton weighs 1600 times as much, it will acquire 40 times as much momentum.
@Thomas Goodey
isnt both energy AND momentum conserved ?
Sure, but they’re not equal. They’re separately conserved.
For instance, energy is conserved within a rocket, so is momentum. But it still moves.
That is correct. If same amount of energy is given to two objects of differrnt mass, the heavier will receive more momentum, in proportion to the square root of the ratio of the two masses.
@Robert Zubrin,
“That is correct. If same amount of energy is given to two objects of differrnt mass, the heavier will receive more momentum, in proportion to the square root of the ratio of the two masses.” ?????????
From Wikipedia
The electric field, E ? in units of newtons per coulomb or volts per meter, is a vector field that can be defined everywhere, except at the location of point charges (where it diverges to infinity).[2] It is defined as the electrostatic force F ? in newtons on a hypothetical small test charge at the point due to Coulomb’s Law, divided by the magnitude of the charge q , in coulombs.
means force F = Eq ; means momentum = force F x
delta t;
means momentums are EQUAL , RIGHT ?
Yes agreed, if the charge is equal, the force shold be equal on both particles. F =qE where E is the field intensity.
https://books.google.co.uk/books?id=qzNdDtZUPXMC&pg=PA75
If the mass ratio is 1831 the ratio of accelerations is 1831. Then delta v = at gives final delta v in the ratio of 1831 to 1, so the momentum change is too, so it seems there should be a net momentum change equal and opposite for protons and electrons. As for the amount of energy, the electron is accelerated more so gets more energy as it depends on the square of the velocity.
However, the electron, traveling faster, would spend less time in the field so would accelerate less, if they both start at rest. S = 0.5 * a * t^2 so t^2= 2s/a so if the ratio is 1831 to 1, then the time is the square root of that so the total change of momentum changes as the square root of the mass ratio.
So – it does seem possible…
They aren’t at rest of course, so the analysis would be more complex. But my first impression is that yes – it does seem possible…
It would depend on the orientation and seems particles would spend more time in the field if it is orientated to slow them down rather than accelerate them. So if it was orientated to slow down the protons aned accelerate the electrons, the advantage would be even greater.
What do others think, is that analysis correct, or am I missing something?
In more detail: the electron, traveling faster, would spend less time in the field so would accelerate over a shorter period of time, if they both start at rest. S = 0.5 * a * t^2 so t^2= 2s/a so if the ratio is 1831 to 1, then the time varies inversely as the square root of the acceleration, so the total change of velocity changes as the square root of the mass ratio. While the energy change is the same for both. For proton m v^2, for electron (1/1831) m (v*sqrt(1831))^2 where m is the mass of a proton. For momentum, for proton mv, for electron, (1/1831) m (v*sqrt(1831))
So energy change is same for both, rather than momentum, which is 23 times greater for the proton.
It would depend on the orientation and seems particles would spend more time in the field if it is orientated to slow them down rather than accelerate them. So if it was oriented to slow down the protons and accelerate the electrons, the advantage would be even greater. If oriented to slow down the electrons then some of the advantage is lost.
^1831 should be 1842 and 23 should be 43 in the above
@Robert Walker
, I looked at your arguments, and you are far more spot on then you can imagine. Assuming the positive and negative ion starts at the center of the grid, then you see that, given the fact that the forces on each ion are equal, the energy given to each ion is equal; simply because the product of the Force and the distance are equal in both cases. Therefore, the energy is equal.
However, the momentums are NOT equal; that’s because the times that each ion resides within the field is considerably different for each ion. I was incorrect in my initial analysis due to the fact that I was looking at a conservation situation involving each ion with respect to the other.
And the conservation situation does not hold in this particular instance.
Great, glad it’s sorted out :). Thanks!
The problem, that forces caused by electromagnetic interaction proportional to electromagnetic field strength and particle charge , also working on very far distance , but do not account charged body mass.
I suppose that you (and author) cannot apply momentum conservation law to this particular case, i.e. when dipole is moving through the some media composed by charged particles (plasma). In this case expected movement can be caused only by electrical forces and stochastic plasma’s (Brownian ) motion , no other (propultion) mass/momentum exchange, It is the basic author’s mistake and it seams to me now, that most commenters in this topic do not understand this fact…
By the way there is lot of other mistakes in this concept, some of it was posted here by other commenters.
My notes about momentum conservation law are related only to the particular case – i.e. proposed dipole drive and fallwing speculations/calculation of expected momentum, i.e. non correct use of this physic law.
To me this looks a lot like the Bussard ramjet, without the nuclear fusion.
I think that as a concept, you are right. It’s possible that the idea, as Zubrin proposed, it didn’t work. But I don’t see any reason why we can’t take atoms in the space, ionize them (if they aren’t ionized already), and used it as propellant.
The difference with Bussard’s is that Bussard’s depends on the mass captured to fusion it, so very specific drag/fusion must be achieved to reach “unlimited range” capability (where fusion propulsion & drag are balanced).
It this concept, it don’t apply because energy is not the base of the propulsion. Joined with other concepts like energy beamed like in a laser sail, this could work.
I think that the key here is that, with special configuration, we could turn space atoms into a auxiliary propellant instead of pure drag.
If the atoms are repelled in the opposite direction when the ship passed, the ship will be accelerating instead of decelerating.
The more mass you push, the better ratio thrust/energy you have.
For interplanetary this idea is not interesting as a bussard like idea, but for interstellar, if you go faster, you encounter more and more mass that, if with the correct configuration helps instead of drag, it could help to raise specific impulse (like in our atmosphere, we use air as main propellant and not the fuel itself).
I really appreciate Dr. Zubrin’s post here, as it expands on his talk and addresses some questions I had with the device.
In my ignorance of the technology, I am missing the knowledge on what conditions allow the protons to pass the +ve shield and be accelerated by the -ve shield in one condition (Fig 1), but be reflected by the +ve shield in another (Fig 2).
As the acceleration of the drive is quite low, especially in interplanetary space, I wonder if there might be a role for “plasma scoops” to focus more particles onto the shield.
As particle density is important, this might well be a candidate for a drive using particle beams to increase the acceleration potential.
Given the scaling possibilities, it seems that a CubeSat with this drive could be easily manufactured, deployed and tested with very low cost.
As regards deployment, as the wires are so delicate, perhaps it is worth the mass penalty of putting the wires on an inflatable structure to deploy them from a compact state for testing purposes. For large structures, rotation seems like a good way to proceed. The mesh would look like a spiderweb with small masses at the end of the radial treads.
Dear Bob
Very interesting concept. I see this as a possible second stage for an interstellar solar sail. Of course, the proton density of the local interstellar medium is a lot less than the value in your illustration. If power-beaming technology of Project Breakthrough pans out, this might be how the necessary s/c power is provided. So I hope that the Dipole Drive proves feasible. All the best with it!
Regards, Greg
I like this concept! I really do!
It seems to be a new and relatively refreshing idea that I don’t believe it. I’ve ever heard about in any other venue. Who is the original originator of this particular idea? Does anybody know?
The distinct advantage that I see behind this is that you take advantage of ubiquitous space ions which (I presume) exist virtually, and freely appear to be a fairly common feature of the outer space environment. It only necessitates that one carry some type of electrical power source that you can readily tap into to provide the electric field necessary to create your propulsion.
The only disadvantage is that I see here within the concept is the idea that:
1. The craft obtains a sufficient velocity and begins to encounter other external drag factors which can limit (which I presume) are present in the environment.
2. The very electrical charge that you used to obtain your field effect would (seemingly almost by necessity) extend beyond the boundaries of your sail and would interact perhaps in a non-predictive manner and would result in both drag and perhaps torquing effects. But that is totally speculative. Otherwise, the compactness and simplicities speak well for the concept in and of themselves.
This is only one disadvantage of dipole drive (as it is dexcribed by author) – modern physic dies not allow it to create any thrust.
Good point – this drive probably can be used as vacuum tube to amplify ETI radio signals …
” Who is the original originator of this particular idea? ”
No idea. I thought it up back in the early 70’s as a bright teenager brainstorming potential interstellar propulsion technologies. but then immediately rejected it because the thrust was so very low. (Had a whole stack of 3×5 card with goofy ideas. Haven’t seen it in decades.) Admittedly, I was analyzing it at lower voltages with both ion species assumed to pass through the grid. It didn’t occur to me to analyze it in a reflection mode.
I suspect it’s one of those ideas that occur to a lot of people, and get dropped immediately without any substantial analysis.
“Unless much lighter power systems can be devised than currently anticipated however, they would still require centuries to reach the nearest stars. ”
What’s wrong with centuries? It’s millennia that start becoming impractical!
“(Aluminum 40,000 psi, 2700 kg/m3, compared to Spectra 400,000 psi, 970 kg/m3.)”
You slipped there. Don’t mix unit systems!
The idea of this system is very clever.
Although it make sense to me, but I think the accumulation of electron on the one side of the payload will quickly neutralize the potential. The dipole is described as two electrostatic grid with no current flowing. I do not see where the power requirement is calculated from. What mechanism is used to feed the power into the system?
Maybe the power requirement is to compensate for the electron accumulating on the positive side? I think something is missing in this concept (or the description of it).
Wouldn’t the electrons ejected forward help to attract protons and deflect electrons in the solar wind, improving the performance?
I will try again…
Quote from autor’s article:
“because the mass of a proton is about 1842 times as great as the mass of an electron, the thrust of the proton current will be about 43 times greater than the opposing electron current thrust ”
Sorry, but it is the false conclusion, electristatic forces for positive (protons, ions) and/or negative charged particles (electrons) and also forces applied to Dipole electrodes are equal, so no any thrust can be expected from this concept.
Agreed. In the case of a stationary (with respect to plasma current) scenario the reaction forces due to accelerated cations and electrons would be balanced. However when the + screen is moving into a plasma wind, acting as a proton scoop, one would expect no electrons to be entering the – screen (from the opposite direction) to generate a balancing force. An unbalanced force will cause an acceleration. So perhaps this concept still has some application after all?
I suppose that this particular Dipole (as it is described by author) will not move even if it will be placed into tha plasma composed by charged particles that all have the same charge (i.e. protons/cations only, or electrons/anions only) :-)
The charged particles contained in the Earth’s magnetic field, e.g., the Van Allen belts are within Earth’s gravity well. Consequently, Zubrin’s dipole drive can’t reach escape velocity without the addition of chemical propellants. Also VASIMR is much smaller, and even with only 500 KM power source it uses today, the VASIMR is faster than Zubrin’s dipole drive. VASIMR already works, is proven and built and ready to go to send astronauts into deep space.
No, the charged particles are simply the ionised free molecules in the thermosphere and ionosphere. A bigger problem is that the further from the surface, the lower the ion density becomes. To reach escape velocity (leave earth orbit), the best strategy would be to activate the drive during only during the closest approach of the earth where the ion density will be highest and the vessel will also travel the fastest.
Excuse 500 KW power source.
The VASIMR engine has taken some 20 years to reach TRL 5 next year. Several of the commentators here are not sure if the theoretical basis of this engine is sound. I do hope to see this in my lifetime
Wall of text. Submit to a legitimate peer reviewed Journal please.
If Robert Zubrin didn’t exist, NASA would need to engineer an replacement at high cost! Always a pleasure to read his work!
Though I think I found a very very minor typo: I guess the voltage of 2028 should be 2048 volt instead (as the author goes stepwise from 1 volt by doubling the voltage multiple times).
The interesting question is if accelerating electrons and protons would accelerate an spacecraft (or if the forces would cancel out), as some have pointed out here.
First of all, I need to look up why ion thrusters tend to use heavy ions (as initially I thought: “Duh, ion thruster use heavy ions for a reason”):
It is the ratio between ion mass to ionization energy. As the ionization energy (as far as I know) depends on electron orbital energies, and should stay (within less than an order of magnitude I guess) roughly the same, ion thrusters favor heavy ions (e.g. Xenon).
For the dipole drive, this is not the case: the protons (and electrons) are already “ionized”.
So would accelerated protons and electrons impart a different force onto the spacecraft?
Both electrons and protons see the same force, giving different accelerations:
a = f / m
f = a * m
The electron will get accelerated 42 times as much, imparting on both the same energy *PER TIME*.
ae = f / me
ap = f / mp
ap * mp = ae * me
mp = me * 42
ap * (me * 42) = ae * me
ae = 42 * ap
But the electron will leave the field much faster. How much faster?
The time is given by:
t = d / ( 0.5 * SQRT( 2 * a * d ) )
If we set the distance d to 1 meter, and the acceleration of the proton ap to 1 meter per second squared we get
tp = 1.41 seconds
With ap of 42 meters per second squared
te = 0.21 seconds
tp / te = 6.48
So as a rough estimate (neglecting the real acceleration in a real electric field) the energy imparted onto the proton should be 6.5 times the energy imparted onto the proton (and conversely the energy imparted into the spacecraft).
Of course, this was just a quit “back of an envelope” calculation, I could be wrong, I could be missing things, …
Should read:
With ae of 42 meters per second squared we get
te = 0.21 seconds
Damn, used the wrong ratio of 42 instead of 1842.
Egg, meet face.
My point still stands, while the numbers are obviously wrong.
So for d=1 meter and ap=1 meter / second squared we get
te = 0.03295 seconds
and
tp / te = 42.9185
Sorry to disturb you, but energy imparted to proton will be always same as energy imparted to electron… it is physical law, if during your caclulation you got to opposite conclusion, you should return to the beginning and make it again , till you will get equality.
Meanwhile I see that many commenters confused by comparation between two unrelated things, it is same as comare equality between “round” and “green” :-)
By the way, why do you compute acceleration of proton and electron?
Why don’t you compute dipole drive acceleration from the same forces?
According your (and Zubrin’s) approach and conclusion dipole drive will get much higher acceleration than electron – because Dipole drive has mass multiple orders higher than electron or proton :-)
Simple open your mind and forget physic.
AlexT:
You need to brush up on kinematics!
Please be so kind to take time to understand these topics before posting again.
1. An electric field will impart the same force on an electron as on the proton. So it will accelerate the (light) electron much much stronger than the much heavier proton.
Acceleration = Force / Mass
In layman terms:
The electron will fly off (out of the field) very very quickly, while the proton lingers much longer in the electric field.
So the electron will experience the force only for a very very short period of time, while the proton will experience the force much longer.
2. Force is equal to opposing force.
In layman’s terms:
There is the force acting on the spacecraft you inquired about.
My sincere apologies but your phrase (quote following): “the energy imparted onto the proton should be 6.5 times the energy imparted onto the proton”
Has nothing common not with kintecis, nor with physic in our Universe.
Some notes on you calculations:
The kinematic energy that charged particle will collect (loose) moving in electric field (let suppose for simplicity it is moving in direction of electric field vector) can be calculated by two “alternative” ways (equations):
1. W = Q * U / 2, where:
Q – is charge of particle (Coulomb)
U – potential difference (voltage) along measured way (Volts)
2. Purely kinematics equation:
W = F * S, where
F – force applied to particle (Newton)
S – distance that particle “travels” in electrical field (meter)
So wandering how can you get to conclusion that energy collected by proton will be higher than energy collected by electron , when both moving in the same electrical field along the same distance…
As I see it, the energy depends on the charge and the voltage so is the same for both however, the momentum imparted or taken from the craft is not. Consider two ways to thrust with the same amount of energy. First, a laser beam and second, a chemical reaction of rocket fuel. The laser imparts orders of magnitude less momentum to the craft for the same energy release than does the rocket fuel. That’s too bad since it would be easier to just shine lasers. The difference between electrons and protons is less but still large.
@Robert,
Laser beam transfer its own energy to the sail when photons are reflected from the sail’s surface – this event there is mass-energy exchange between the beam and spacecraft, that will create force/acceleration.
In chemical rocket we have energy-mass-mometum exchange when rock?? “looses” it’s mass with high speed.
In the described dipole drive :
– the dipole does not reflecting an energy beam
– the dipole does not “loose” mass
– the supposed source of acceleration of the dipole is electromagnetic interaction between grids and stochastically flying in the interstellar vacuum charged particles , this interaction is depends only on the voltage between electrodes and particle charge, initial speed of particle, speed, direction, mass are not important in this case.
– the free flying charged particles that will be fully reflected by this dipole will not create any thrust too, because will be applied (statistically) in the same amount, from the both sides, both polarities.
– the solar wind can create some thrust if positive grid will have enough charge to reflect it, but in this case solid metal electrode will work many time more efficiently that the grid…
Your analysis is I believe quite correct, even if you have made a calculational mistake.
However, in thinking this over just a bit more I began to wonder whether or not this particular concept may suffer from one small flaw.
If you are accelerating charges with the intention of creating force on the spacecraft you have a situation in which you have spatial charge separation, which inevitably do to charge buildup begins to create an external field. How such a charge separational field should interact with the grid and perhaps begin to neutralize its accelerational properties remains to be seen. It may be expensive enough, this charge separated field to in fact, nullify the ability to accelerate the space plasma, as well as possibly create facts with the space plasma that is to enter the grid for acceleration.
If you think that next Tony’s calculation is correct:
“the energy imparted onto the proton should be 6.5 times the energy imparted onto the proton”, you think you should not be bithered by any “charge separationsl field” , everything is possible in the Universe , that is not limited by first law of thermodynamics.
I have been thinking about the opposing force created by the external field, and my very very rough back-of-an-envelope-guesstimate is that the opposing force of the external field will be about one third (1/3) of the desired force created by the internal field.
So for every Newton the internal field creates, the external field will give an opposing force of about 0.33 Newton – give or take…
My reasoning goes as follows:
First we take a 2D view of the two poles (the two plates of the “capacitor”)
Then divide the area by four lines:
– Two lines through the plates
– Two line at the ends of the plates, at 90 degrees to the plates
(This should work in 3D as with planes as well, but 2D is simpler to explain and visualize)
Now we have 9 sections: The internal field in the middle, surrounded by 8 sections of the external field.
The external field consists of the following sections:
– One section “in front”, and one section “behind”, both roughly with field lines going in the wrong direction. (Boooo!)
– One section “on the left”, and one section “on the right”, both roughly with field lines going in the right direction. (Hurray!)
– Finally there are the four corner sections, where the contribution of the field lines cancel each other out. (We can live with that.)
If we are pessimistic, we say that the sections “on the side” don’t matter because they are so small, and for the other 6 external sections we end up with about 2 out of 6 where the field that contributes to an opposing force – so this is a very rough estimate that yields an opposing force of one third of the force created by the internal field. But we would need to go and put different spacecraft geometries into a simulation to see what effect different plate size to plate distance ratios have.
AlexT:
If you can not contribute anything meaningful besides scathing cynicism, why do you not stay quiet?
And why are you so impolite anyways? If you are right, you can calmly explain why you are right and why we are wrong.
After all, if we are as wrong as you say, we should be able to embarrass ourselves without your help.
And until you start to contribute something meaningful, I will ignore you.
Charley: I have been skeptically wondering along similar lines of thought – my gut told me reality could be be harsher.
With regards to field neutralization, I think this will be a no problem in reality. Only on very long distance flight (think interstellar), one might get problems with the deposition of protons on one dipole, or erosion of the other pole … that is not a question the back of an envelope can answer. But other than that, on “short distances” I think maintaining charge separation should be no big obstacle.
With regards to the external field: That is a much more interesting question, and I fear this could bring down the actual efficiency of the dipole drive by quite a bit. This is a question simulation should be able to answer.
Charley, after some more thinking about this, I think I was wrong about the “1/3 opposing force” of the external field.
The external field will cancel itself out (or even create a little additional desired force) – as far as I see the external field should not create any problems with regards to thrust.
The field lines go in one arc from one plate around the spacecraft to the other plate. On each field line you can mark two “reversal points” where the field line is parallel to the poles/plates. With this we can divide each arc into three sections:
– First one arc-section from the pole/plate to the first reversal point (with the field lines pointing in the wrong direction, giving force in the wrong direction)
– Then an arc-section from the first reversal point to the second (with the field lines pointing in the right direction, giving force in the right direction)
– And finally the arc-section from the second point to the other plate (and again wrong direction of field lines, giving force in the wrong direction)
Now, we can ignore the “sideways” component, because for every field line on one side of the craft, there is a field line on the other side of the craft.
That leaves us with the component parallel to the acceleration axis. And if we take only that component, then the (undesired) component of the first arc-section, plus the (undesired) component of the last arc-section (plus the pole/plate distance!) is equal to (desired) component of the second arc-section.
So roughly the two forces created by the external field (one against the thrust of the spacecraft, and one in direction of the thrust) should cancel each other out.
Precise numbers would need a simulation, but I expect that the residual force by the external field is much much smaller than the force created by the internal field (and the force might even possibly be in the desired direction).
There is additional problem in the Dipole drive concept , it is described in cytate below:
“In Fig. 1 we see two parallel screens, with the one on the left charged positive and the one on the right charged negative. There is thus an electric field between them, and effectively no field outside of them”
The physic teach us that outside electric field of described dipole (in reality – it is classic parallel capacitor) will be close to zero for distances from outside surface of electrode that much bigger than distance between elctrodes , when distance from charged particle to outside surface of electrode is comparable with space between anode/cathode electrical field will have huge inluence on charged particle, so proton will be repelled by external surface of positive plate and after proton will pass through “dipole” it will be attracted by negative plate… (this force will be in opposite direction to supposed “thrust”)
Further speculation you can do by you self…
Yes, the net zero charge is a far field approximation only. There is no magical boundary established by the first screen, just a local maximum of the net charge along a path normal to the plane of the screens. With the large (multiple meter) spacing of grid wires being specified the local maximum should not even be large.
“The physic teach us that outside electric field of described dipole (in reality – it is classic parallel capacitor) will be close to zero for distances from outside surface of electrode that much bigger than distance between elctrodes, when distance from charged particle to outside surface of electrode is comparable with space between anode/cathode electrical field will have huge inluence on charged particle”
Please do us all a favor and read some high-school physics book before embarrassing your teachers so badly again.
https://www.youtube.com/watch?v=XSXKk_A3xUM
Dear Antoni,
This youtube’s high-school lecture try to make theory and studying little bit simplier for a students. So it talking only about the case when capacitor is composed by two infinite solid metallic surfaces with equal (even) charge dustribution, as sequence it talk nothing about the case when capacitor has limited size, plus capacitor’s plates are composed by grid, but not solid surface, grid means there will be not equal charge distribution etc.
If I could accept your point of you, I had to conclude that vacuum tube that have more than 2 electrodes should not work in any way…
Dull…
So, how about you have a three grid system?
The grid facing the incoming plasma flow would be negatively charged. The center grid positively charged. And then the third grid, at the back side, would again be negatively charged.
Protons would still be reflected, but electrons would exit the back at their original velocity, thus reducing the power consumption.
So now we have tetrode rather than a triode (the external ion source is the cathode) in a CRT arrangement where the ions pass through rather than hit the anode. At least we don’t need a glass envelope in space!
While I have not even tried to work through the details of Zubrin’s proposal I suspect AlexT is on the right track.
They may be no need for a voltage generator if the material from which the sail is made has a high electron emission due to UV from the Sun.
Michael, I could not let your idea (“They may be no need for a voltage generator if the material from which the sail is made has a high electron emission due to UV from the Sun.”) just sit up on my screen. You may have suggested something that could make a very big difference (including, perhaps, to the history of space travel):
There are numerous photoelectric materials that could, exposed to the unfiltered sunlight in space, “emit their own electrons,” and self-healing (from radiation damage) photovoltaic cells–solar cells–have been developed (but are not, to my knowledge, commercially available yet). Also, thin-film solar cells (which JAXA’s IKAROS solar sail has) are considerably more radiation-resistant than the traditional wafer-type solar cells, and could power a dipole drive for a long time. In addition:
One or both of the dipole drive’s grids (assuming it used only ^two^ grids; more grids might be employed, as in some gridded ion thruster designs) might be made of the electrode materials that are used in alphavoltaic or betavoltaic fission batteries, which produce electricity via bombardment of alpha particles or beta particles from suitable radioisotopes (the atomic batteries used in some heart pacemakers operate in this way) might also be used to generate electricity for a dipole drive. Instead of utilizing an on-board radioisotope (although such a radioisotope film *could* be painted or otherwise cemented onto the electrode material grids if desired), the ambient cosmic rays, solar/stellar wind particles, and (within a planet’s magnetosphere) radiation belt-trapped particles could be used (via their bombardment of the grids’ electrode material) to generate electricity for the drive.
As I stated above, the mere fact that you are performing charge separation to obtain net acceleration of the craft may be enough to nullify the accelerating potential between the two grids (due to the accumulation of external separated charges outside the grids).
That’s why I believe whenever you have an ion drive, in which the latest manifestation of this uses the noble gas xenon, you ionize and accelerate the ions through a charge grid just before the exhaust is exhausted into space. You do so because then the positive ions are neutralized by the negative grid and you have neutral exhaust. I’m not seeing this type of neutralization in this particular scheme; and that may create the charge separation problems that I’ve just spoken of.
That echoes my own misgivings on the idea. I think Jim Benford was making a similar allusion. Charge separation is the whole point of the Drive – a potential difference to push ions in convenient directions – but one doesn’t shed excess electrons into the surrounding plasma environment without consequences. The question is whether the Dipole Drive gets away with it because the Solar Wind plasma is essentially collisionless. Would the net result be a bubble in the Solar Wind? I suspect that only in-space tests would answer the question, as such plasma physics is challenging to simulate on computer or analyse with our mathematical approximations.
A fascinating concept, but I am with Jocelyn Boily above: how does energy (power) get transferred from the power supply to the protons?
A small amount of energy is used initially to charge up the two grids and create the electric field. Thereafter protons passing through increase their energy. How does this energy get from the power supply to the protons? Electrons are ok – they are reflected with a change of direction but no change in energy.
Energy for the protons (as well as electrons) come from the extraction of the energy from the electrical field that’s created via the grid. The Power source in turn keeps the grid at the respective potential required for operation.
Yes, the power source does keep the grid at the correct potential. But after the voltages, the electric field and the charges on the grids are set up there are no more currents flowing and the power supplied to the grid is zero, because power is voltage times current, and the current is zero.
So where does the kinetic energy given to the accelerating protons and electrons by the electric field come from? The answer is that no energy is supplied overall. As I note in a comment below, what is missing from the analysis is the curl B field caused by dE/dt (= dE/dx x V, where V is the velocity of the particles entering or exiting the field from, or to, outside). These B fields cause the particles to change direction and slow in the direction of the electric field, and Conservation of Energy implies that the speed of the particles are unchanged after exiting – just the direction is different.
Consequently the Dipole Drive produces much less thrust than was originally thought.
“But after the voltages, the electric field and the charges on the grids are set up there are no more currents flowing and the power supplied to the grid is zero…”
not true; flowing pos and neg ions ARE the currents …
“not true; flowing pos and neg ions ARE the currents …”
They are not, however, going in or out of the power supply, which is hence not putting out any power to accelerate them.
I have refined my ideas a bit on the physical mechanisms at work. If, as the protons move between the grids (and forming an electrical current) they are accelerated, a changing magnetic field is produced because the current increases, and also, via the Maxwell-Faraday Law, an electric field that opposes the accelerating field. There will also be eddy currents that dissipate energy in the material of the grid. The overall effect is that there is no thrust – just drag.
There will be some electromagnetic field oscillation when charged particle is approaching, passing through and moving from the grid, the forces ouside the grid will have opposite direction to the force inside the grid, so in ideal approximation the summary energy should be equal to zero, in non ideal approximation charged particle and dipole drive will lose their energy through electromagnetic waves and internal heating, so as result the dipole will get some momentum from charged particle but it will be pointed to the direction that charged particle had before it was interacting with the dipole grid , but it will not be in direction expected by author.
VASIMR is at TRL 9 this year: https://www.nextbigfuture.com/2018/03/advanced-vasimr-plasma-drives-and-spacex-bfr-trip-times.html
This article states that vasimr is at trl 5 or above. Since it hasn’t been flown in space yet there’s no way it’s close to trl 9
https://thecostaricanews.com/canadian-space-agency-signs-us-1-5-million-rd-agreement-boosting-ad-astra-rocket-companys-vasimr-development/
At what MW level?
AFAIK, the VASIMIR test at the ISS was canceled because the ISS can’t supply that power level.
When I read about VASIMIR, I keep keep reading about power levels of 20 MW or even 200 MW. How do you intend to power such a VASIMIR engine? How much mass do you have to allocate to a power source (solar panels I presume)?
A good material for the mesh would be capillary filled and joined nano-tubes, very light weight.
https://www.nanowerk.com/spotlight/spotid=6371.php
The 39 day mission to Mars using VASIMR propulsion takes 200 Megawatts total input power driving 4-to-8 yet to be designed VASIMR engines that will sink 25-to-50 MW each.
This is sheer and highly purified fantasy. Whey do they keep on talking about a 39 day mission to Mars when such power levels are barely in the realm of speculation? The VASIMIR seems to be more of a hype drive than hyper drive.
My apologies, this response was meant for the VASIMIR post above.
I see absolutely nothing wrong with a 200 MW power source; nuclear thermal rockets probably produce far greater amounts of usable thermal power just during their brief operational period. I think probably that if anything is going to be accomplished with regards to VASIMIR , ultimately one’s going to have to resort to a nuclear option to produce anything of substance.
Agree in that a nuclear reactor can generate copious amounts of thermal energy. The but is using a heat engine to extract energy in the form of electricity. A 200 MW electrical output would require radiating perhaps a gigawatt of thermal energy. in the vacuum of space. Daunting to say the least.
An MHD-based electrical supply in which the exhaust carries away the necessary vast quantity of heat could alleviate this issues but that technology, IMHO, lies decades or scores of years in the future.
Russia has announced a megawatt class spaced based reactor system that MAY undergo flight testing within a year. Hope it happens but not holding my breath. The following link is not very informative but better than other garbage links:
http://www.spacesafetymagazine.com/aerospace-engineering/nuclear-propulsion/russia-developing-nuclear-space-engine-2017/
“I see absolutely nothing wrong with a 200 MW power source”
Really?? What about weight?
https://www.youtube.com/watch?v=myYs4DCCZts
Actually, the weight factor is not a great as factor as you might possibly believe. I know personally of a operating research reactor, which is cool by pressurized water, which has a maximum power output of 10 megawatts. The entire reactor itself occupies the same volume that you would see in a relatively large ground coffee container that you might see in the American grocery store. I would estimate that in terms of nuclear material, you might be looking at maybe at the most 200 pounds of enriched uranium
I believe I can answer my own question above. When a proton both enters and exits the electric field it ‘sees’ a large changing electric field which creates a magnetic field transverse to the electric field (Maxwell’s equations). This magnetic field acts via v x B forces to change the direction, again transverse to the original direction of motion, and so there are two impulses opposite to the electric field thrust. Without doing any math, my guess is that the overall effect is that the proton just changes direction and there is no net increase in speed. This means the thrust will be less than that calculated using the electric field alone.
Would the nearby medium become charged by the drive in a way that’s detrimental to the setup? I don’t know how much would be absorbed vs flying on past. I imagine you would be kicking off a bunch of charged particles into the direction you want to travel and behind, that would act in a negative way. Basically would that sort of close the system?
That’s my chief concern: I’d expect protons to pile up in front of the sail, and be depleted behind it. This would, at least partially, cancel out the field of the grids.
The system needs a full simulation, there are too many things going on to derive the performance from a basic pencil and paper analysis.
I may be missing something, but I think the thrust from this all comes from the approximation of a parallel plate capacitor’s field as uniform between the plates and 0 elsewhere. The actual field looks like this: http://farhek.com/a/a/em/em-beauty-the-parallel-plate-capacitor-electric-field-distribution-of-two-oppositely-charged-metal-plates-colors-represent-magnitude_electric-field-of-a-capacitor_10nf-capacitor-hvac-start-.jpg (If that image link doesn’t work, just do a google image search for “parallel plate capacitor electric field” and look at the one that is a blue-to-orange gradient.) The non-approximated electric field has a strong, roughly uniform electric field going one way between the plates but also a weak but large electric field going the other way outside the plates. I am not entirely confident, but I think these would cancel each other out for a charged particle making the journey from far away, across the plate, and far away again.
I would love to be wrong about this! Possibly the plasma somehow interacts with the large, weak field to make my reasoning wrong.
@Peter Reid,
You are absolutely right.
Sadly, but this mistake is not single one in the discussed article.
“The non-approximated electric field has a strong, roughly uniform electric field going one way between the plates but also a weak but large electric field going the other way outside the plates.”
The field will be very strong between the plates and only a fringe field at the edges, I think you are thinking of a magnetic field setup.
The problem is not the edges. The problem is the large dipole field that emanates from the backsides of the plates and extends into infinity. It has the effect of slowing down arriving charges exactly by the amount they are accelerated while between the plates.
The electric field is a conservative force, meaning the energy provided to a charge is path-independent and can be described by a potential. In any physical situation, the potential is constant at infinity. Charges both coming from and going there can gain no net energy, no matter what path they follow and no matter the field configuration as long as it is static.
“The non-approximated electric field has a strong, roughly uniform electric field going one way between the plates but also a weak but large electric field going the other way outside the plates.”
Only near the border of the plates. For very large, close plates, that border field is not really important for this use.
The Discussed dipole is not so large to be accepted as infinit surface and it has “plates” that are not solid surface but metallic grid, grid has many-many edges and distances between grid wires is many orders bigger than size of charged particles…
Your reasoning is correct.
This conversation is noisy and bordering on the impolite. I do wonder about a massive influx of solar protons from a CME. Can such a drive in interplanetary space experience a (helpful) surge in acceleration? Can this drive provide shielding to the space craft?
Regarding the relative thrust between two particles with the same kinetic energy but with a mass ratio of 1600+, the heavier particle would have a velocity about 1/40 of the lighter particle but 40 times the momentum. That is high school physics. I suppose the basic question is whether the drive would actually create similar kinetic energies in protons and electron. If so, it will produce the predicted thrust withstanding all of the other factors discussed above.
I share your concern about the tone of the conversation. The best thing to do when things get heated is to remember the posting rules on the front page of the site, and in particular the injunction ‘civility counts.’ This is by way of a general admonition to keep the tone constructive, and is not aimed at any particular individual. Debate and disagreement are welcome, but let’s keep it civil.
Overall, the short statement of the comment policy is:
“Centauri Dreams publishes selected comments on the articles under discussion here. The primary criterion is that comments contribute meaningfully to the debate. Among other criteria for selection: Comments must be on topic, directly related to the post in question, must use appropriate language and must not be abusive to others. Civility counts. In addition, a valid email address is required for a comment to be considered. Centauri Dreams is emphatically not a soapbox for political or religious views submitted by individuals or organizations. A long form of the policy can be viewed on the Administrative page. The short form is this: If your comment is not on topic and respectful to your fellow readers, I’m probably not going to run it.”
I believe that people here are being impolite to one another, I’ve been on threads that get extremely heated and this is nothing!
I can see, and understand that once a position is taken. If you suddenly realize you are incorrect, it becomes very difficult to back out of the position without embarrassment. Believe me, it’s happened to me more than I care to admit!
Please, let’s not stifle a intellectually rich back and forth simply because somebody seems to stand their ground…
“I believe that people here are being impolite …”
Sorry, I meant to say that “I believe that people here are NOT being impolite …”
‘the basic question is whether the drive would actually create similar kinetic energies in protons and electron.’ Yes that is a reasonable question. Consider in the case where the dipole is already moving to the left as diagrammed. The positive cation travels a shorter right-ward distance through the E field (the grids are moving as a unit to to the left), than does the electron traveling a longer distance left-ward distance through the same E field. So one would expect the work/kinetic energy of the accelerated electron to be greater than the work/kinetic energy of the accelerated cation. How much so depends on the relative speeds of the dipole/grid structure and the ions. I think it plausible that a moving dipole could generate thrust but how much, and under what conditions, I’m not entirely sure.
“This conversation is noisy and bordering on the impolite”
I agree with you, sometimes people get excited and forget their manners.
I am rather surprised at the intensity of the criticism that this concept has attracted from some quarters. At the very worst (which I don’t necessarily think is the case), it would seem that modifying the arrangement of the dipole drive to be like that of a gridded ion thruster (including an exhaust beam neutralizer [an electron gun or a hot cathode filament], placing a ring-shaped electromagnet coil between the screens, etc.) would ensure that it would work, and:
Making the screens spin-rigidized would help prevent the oppositely-charged screens from being electrostatically drawn toward each other (dielectric spacer rods at the edges, and at other points between the screens, would also help to keep them separated). While all of these features would, of course, add mass, making the dipole drive very large would make those added parts a smaller percentage of the total mass; a spin-deployed-and-rigidized dipole drive could be miles across–also:
Given even Dr. Zubrin’s original dipole drive’s similarity to a gridded ion thruster (multiple-grid ones have been tested–one 1960s-vintage Martin-built ion engine had five grids), I wonder if a Hall Effect thruster analog of the dipole drive might produce more thrust than the original dipole drive, all else being equal? (Hall Effect thrusters usually produce more thrust than comparable gridded ion thrusters, at lower specific impulse [lower exhaust velocity].)
The third problem with this concept :
Direct current calculation, the current between electrodes can be caused by two things:
1. Charged particles that “fall” directily to electrodes
So if we accept that plasma dencity used in authors calculation are currect, expected constant currecnt will be much lower than used in this calculations this current is function of voltage between electrodes, relation between cunducting area vs. electrode’s free space area and particle motion vector…
2. Alternating current, that is caused by electromagnetic disturbance from charged particles that are pasing through the Dipole (particles that are not thouching electrodes). Calculation of this current is complicated electrodynamic task.
The concept results in usable thrust. But it’s pretty feeble. I suspect VASMIR might be more efficient. Hardly surprising since VASMIR uses its own plasma source.
I’m dismayed at the number of people who cannot do high school level physics and yet feel compelled to promulgate false narratives. The energies of protons and electrons are equal, but their momentum is not. The momentum imbalance is what provides net thrust.
Isn’t the energy to ionize the propellant a significant fraction of the total energy of the VASIMIR drive? If so, the Zubrin drive would have an advantage as its propellant is already electrically charged (previously pointed out by others). The inefficiency resulting from electrons producing a retarding thrust could be negligible.
Regarding the concern of electrons piling up in the upstream direction and essentially starving the grid of protons, would not coulomb repulsion disperse the electrons? Or could the grid have a modest curvature to impart a velocity vector that would disperse the electrons? Believe me, I am not an expert or even a novice in this area but hope these comments will trigger conversations from those who are.
“I suspect VASMIR might be more efficient. Hardly surprising since VASMIR uses its own plasma source.”
On the contrary, that makes VASIMR hugely less efficient, since it has to carry its only propellant, and thus the exponential increase in mass of the rocket equation applies.
Obviously the details of the mission matter. Something could be technically more efficient and practically less useful at the same time.
May be you right, but till now none of comenters that know well physic could not explain how charged particle momentum is transferred to the dipole acceleration.
Yes proton’s momentum will be higher, so what ?
Finally I understood where is the basic mistake in Dr.Zubrin concept.
1. After acceleration in electrical field of dipole proton and electron will have equal energy. It is correct statement.
2. Kinetic momentum of proton will be ~43 times bigger than electron’s. It is correct statement.
3. Now about the basic mistake in concept – you cannot apply to proton-dipole interaction principles that are applied to calculation of two rigid bodies impact in mechanic !!!
Let ignore the case when charged particle “falling” directly on electrode grid.
Let think about charged particle that passing through both electrodes of the dipole.
In this case charged particle and the dipole are never have full exchange by their kinetic energy!!!
Charged particle and dipole have only electromagnetic interaction. For simplicity we can accept that is limited by only electrostatic forces,
i.e. they exchange energy according electrostatic laws …
So, Force applied to charged particle (and the dipole) can be calculated by equation:
F = E*Q, where:
E – electric field strength, in V/m
Q – electric charge in coulombs
Only this force could create thrust in this case.
Energy that charged particle (and the dipole) will collect during “travel between electrodes is calculated by equation:
W = Q * U / 2, where:
Q – electric charge in coulombs
U – voltage between electrodes
Because electron and proton have the same charge – the electrodynamics forces interacting between pairs proton-“the dipole” and electron-“dipole” are same, but have opposite direction, as sequence the dipole will have equal thrust from electron and/or proton (pointed to opposite directions) and in neutral plasma forces will be compensated – i.e. no drag…
You can apply kinetics momentum transfer laws only to the case when charged particle directly impacts electrodes, in this case there is exchange of kinetic momentum between the dipole and charged particle (and momentum conservation law can be applied)…
P.S. I intentionally ignore here, the case when charged particle moving in the near field of outside surface of electrodes.
On small distances (comparable with between electrodes space) Electrical field is not Zero, as supposed in concept, and there will be charged particle deceleration and acceleration,
it is another problematic story about this concept.
Small correction.
The statement in paragraph 2 will be correct only for the case when start speed ( in direction perpendicular to electrode surface) of electron and proton are close to zero.
I believe it’s apparent that the two greatest contributors within these lines of arguments are converging into a single viewpoint as to the momentum/energy realm of understanding.
As for myself, I initially started this particular examination of the problem believing that the momentum of both particles were equal; on that I was mistaken. However, I do agree that the energies experienced by the positive and negative ions do in fact equate.
Of more importance than the fact that the positive ions contribute by far the greater bulk of the thrust than those of the electrons is the far more serious and impactful question is to whether or not the separated ions accelerated through the grid begin to form opposite and opposing charged clouds that surround the spacecraft.
Has Zubrin considered whether or not these opposing charged ion clouds will in fact ultimately result in nullifying any acceleration that can result from utilizing the native plasma that exist in outer space ??
As I stated previously, Ion drives seek to accelerate one species of ion which it then neutralizes at the exhaust grid, such that you have a neutral species actually being vented into space; that way you do not obtain opposing sources of charge, which will seek to neutralize any momentum obtained by your exhaust stream.
I think that this particular issue could be a showstopper with regards to the entire process, but I would like to hear Doctor Zubrin’s opinion on this.
I suppose that cosmic charged particles has initially multiple orders higher initial speed and energy than can get from 64V electric greed field (or even 1024V), so most of them will successfully pass through grid changing their speed vector (trajectory) little bit, so particles will fly away.
When charged particle flying through the dipole, it’s energy and kinetic momentum is not so important in this device, because there is no any direct impact between particle and the dipole drive, there is no any traditional for classic kinematic mass-speed exchange, only electromagnetic interaction.
This interaction is more similar to fly of rigid body through viscous liquid body, something like fly of gun’s bullet through gelatin.
“Has Zubrin considered whether or not these opposing charged ion clouds will in fact ultimately result in nullifying any acceleration that can result from utilizing the native plasma that exist in outer space ??”
It’s already explained in the article. Please read it again.
One thing I find fascinating with this drive is that it initially could act as a drag device to get started from rest, but eventually as its velocity exceeded the solar wind, outrace it. Zubrin solves the problem of the device reaching the same velocity as the solar wind and being “becalmed” by using a tacking maneuver.
The arguments over whether the device would have a thrust or not seem rather reminiscent of the wind-powered vehicle that was designed to go faster downwind than the wind. Although this seems unintuitive and impossible, it has been achieved. The discussions also got rather heated.
This dipole drive can be tested on Earth using the experimental setup used to test the plasma magnet. A vacuum tube with a “solar wind” provides the environment. I suspect the dipole drive would need a very high voltage between the grids to generate any thrust that would be measured with a torsion balance due to the small diameter of the vacuum tube. I look forward to hearing about the results of such tests. Assuming they show the drive does work, then a book on using the drive on the same lines of detail as those on solar sails (e.g. Starsailing) would seem a useful next step.
Alex, thank you for posting the link to that Wikipedia article–I vaguely recalled (but not until you reminded all of us here) hearing about those wind-driven vehicles! The explanation of how they work may indeed be germane to the Dipole Drive, as the article says:
************
Explanation
Main article: Wind-powered vehicle § Theory
Rotor-powered vehicles, like Blackbird, have a drive linkage between the rotor and the wheels. Gaunaa, et al. describe the physics of rotor-powered vehicles. They describe two cases, one from the vantage point of the earth and the other from the vantage point of the air stream and come to the same conclusions from both frames of reference. They conclude that (apart from forces that resist forward motion):[14]
There is no theoretical upper limit to how fast a rotor-driven craft can go directly upwind.
Likewise, there is no theoretical upper limit to how fast a rotor-driven craft can go directly downwind.
These conclusions hold both for land and water craft.
Required for wind-powered vehicle (or water craft) motion are:
Two masses moving with respect to each other, e.g. the air (as wind) and the earth (land or water) to provide kinetic energy.
The ability to change the velocity of either mass with a propellor or a wheel to convert the kinetic energy of the two masses into that of the vehicle.
Depending on one’s frame of reference, the description of how the available kinetic energy powers the vehicle differs: As seen from the earth’s surface, the propellor decelerates the air to accelerate the earth imperceptibly with the wheels or as seen from the air stream, the wheels imperceptibly decelerate the earth to accelerate the air with the propellor.[14]
My own, but unworkable, idea was to use rotating magnetic fields that would deflect and accelerate charged particles, much like a propeller in air. Theoretically, the massless magnetic fields could drive a powered craft faster than the solar wind and navigate in any direction.
If Zubrin’s approach works, this solves some problems, but the acceleration is very low and the advantages of navigation are less impressive given what can be done with solar or electric sails, especially beamed ones. After all, Breakthrough Starshot is targeting 0.2c as a final velocity using “drag” only. Robert Forward’s sails could both accelerate and decelerate with a beam, using the staged approach. If the plasma magnet drive works as advertised, it offers far better acceleration than the dipole drive, although its velocity is limited as a drag device to the maximum of the solar wind velocity. As a solar system drive, it looks far more attractive.
Actually, any voltage in excess of the minimum necessary to reflect most of the protons is undesirable, as you’ve then maxed out the thrust, and the parasitic losses scale with voltage. In particular, higher voltages increase the change in momentum of the electrons, which is a dead loss.
That’s in the reflection mode. Thrust scales with voltage if your voltage isn’t high enough to reflect the protons.
That’s why I suggested a third grid with the opposite voltage, so that the electrons emerge with the same energy they entered with. That should reduce at least one category of parasitic loss. OTOH, it would increase grid current, so maybe not.
Just wondering if the velocity of the spacecraft will have greater impact on the impulse efficiency as it gets closer to the solar wind velocity. As the velocity difference becomes less the opposite charges are more likely to impact the mesh possibly damaging it and not be reflected.
Is there any chance to test the concept? I can’t tell it all, but one contributor suggested building a cubesat to test it. But there would be facilities available that could test it in a small scale? The concept should be easy to verify.
This concept (I mean measuring of thrust created by two grids in neutral media) can be easily tested , for example with tube filled by ionized halogen gas, or even with liquid electrolite (need only correctly choose correct solution, that will contain anions and cations with significantly different mass).
If Dr. Zubrin’s calculations are correct, so With higher density of plasma or electrolite “thrust” will be many times higher ,although I am sure there will be no any thrust :-), but tests are really possible.
A partially ionized gas or electrolyte will also stream neutral particles, just like an ionocraft (“lifter”), a technology that we know works. I think the University of Washington has the setup to test the idea. I’m sure there are plenty of other facilities that can test the idea.
I suppose that vacuum electrical conductivity (resistance) vs. electrodes voltage vs. vacuum dencity is measured already long time ago and can be checked without any laboratory tests , it is key parameter used in calculation of Dr. Zubrin Dipole drive concept.
Sometimes no lab needed…
Isn’t the point to test the device under conditions that reflect space, but also suitable for the laboratory? One is trying to avoid the problems of results ambiguity that plague the EM drive. I would leave the details to the experimental physicists, like the Benfords, to get this right.
The likely problem areas, such as the plasma polarizing on either side of the grid canceling the inter-grid voltage, or interactions with embedded magnetic fields, don’t look to me to be easy to test in the lab.
I could be wrong about that, maybe you could scale down the entire apparatus including increasing the plasma density, and get perfectly representative results.
On the bright side, it should be relatively cheap to test in space compared to many other concepts.
The “corner stone” of the dipole drive thrust calculations – is expected DC current between the grids.
This parameter can be easily tested on the scaled model , with relatively simple and not expensive instruments .
P.S.
I am sure – this current , in reality , will be orders lower than you can read in discussed concept.
So even if everything else is correct in Zubrin’s concept lower current means lower thrust…
And results of current measurement can be so different from given in cocept, so will be no need to make any further (and more expansive) tests.
This dipole drive would still need a conventional rocket with a combustion chamber and chemical propellants to reach escape velocity. It’s too large and slow to ever be considered to be useful for astronauts.
One way to do it would be to launch the ‘main’ spacecraft with the dipole drive, and let it build up speed doing thrusting and gravitational slingshots in the solar system, and then make a final, high velocity pass close by the Earth, outbound, and then a crew could use a very small, light, chemical propulsion craft for transferring crew only from Earth or Earth orbit – for example something resembling the old Apollo Lunar ascent module. Then dock with the main vessel. Fuel, other consumables, and other equipment is already on board and up to speed.
Can the dipole grids double as a radio wave rectenna for beamed power?
This is similar to how ionocraft operate. Could a dipole drive actually be configured to launch from ground level in the lower atmosphere like an ionocraft. Then slowly accelerate to orbital velocities as it ascends to higher altitudes in the stratosphere?
That is an intriguing thought – the dipole with suitable grid spacing and other electronics act as a receiver for high power microwaves. The dipole would use that transmitted energy to drive ion acceleration. Of course, the devil is in the details but it would be sweet if the space craft could eliminate both propellant and onboard power generation – like a solar sail but with the potential for considerably faster acceleration.
An ionocraft: dipole drive
approx equals
turbofan: pure jet.
Ionocraft – is not dipole drive and uses different effects.
If you will continue to call every “drive” that uses two electrodes and electric field as dipole drive, you should conclude that Dr. Zubrin is the “father” of all electrostatic drives :-) even those that are really working and was lanched long time before he proposed the dipole drive concept…
If the grids could be electrically-sectioned using switches, the sections should be usable as a rectenna array (the smaller sections would be naturally resonant at microwave radio frequencies, acting as many small half-wavelength dipoles; they could be made either center-fed [current-fed, as are most dipole antennas] or end-fed [voltage-fed, as are some wire dipole and dipole tower antennas; only half as many switches would be required as for center-fed dipoles]), and:
A famous–or infamous, depending on who is consulted!–example of end-fed dipoles was twice launched into orbit by the millions in the Project West Ford “needles” experiment. The first satellite failed to dispense the 1/2 wavelength long (at the chosen frequency), hair-like, wire ‘whiskers’, but the second satellite did, creating a temporary (until atmospheric drag caused them to re-enter the atmosphere) “artificial ionosphere” that reflected the microwave radio signals.
Switching various parts of the grid on/off or controlling power would allow orientation around the center of gravity, obviating the need for a “tail” dipole as proposed by Zubrin. This is rather like the approach used by the IKAROS solar sail.
I have a little niggle about the design, if say a positive ion comes in it will not see the positive plate because it is cancelled or shielded by the negative charge. Now in the design as the ion approached the positive plate it will be slowed down a little due to repulsion but accelerated as it enters the E field. My problem here is that the plate is actually a very open mesh to allow ions through, but the E field is between the + and – mesh conductors. The effect would be a lower net acceleration because the ion would not see the intense E field as it is between the conductors predominantly.
Zubrin is correct that ions and electrons passing between the grids would produce a net momentum reaction, by exactly his arguments. Residence time is shorter for the ions than the electrons, resulting in a density difference, resulting ion thrust. BUT, I see two flaws as described. Zubrin assumes there will be current through the grid, this is where he assumed the energy is supplied to satisfy conservation of energy, but I see no mechanism for ion current to land on (and be emitted by) the grids unless he simply didn’t mention something. I believe this shows up in another way which solves the conservation of energy: I believe there is a significant electric field outside the grids. It looks like an equal and opposite dipole to me on the largest scale. Not as concentrated a field but with the same potential. Thus ions would slow down to the grid, accelerate through it and decelerate leaving the area, with a net zero effect. Thus energy is conserved considering that none is being pumped into it via the grids anyway. Change this into a hydrogen collector (possibly collecting a fraction of its power from the incoming kinetic energy – current into a potential), pump them into an ion thruster, and you’ve got something.
Oops, I mean electrons reside for the shorter period between the grids. Gah!
Till electric field strength allows electron to pass through grids electron’s reside time does not change anything:
1. electron (proton) will have it’s own evergy that is order higher than it get during acceleration in electric field between grids
2. As faster it will leave “between grids” space, as faster next electron will enter between grids…
1. Likely true of protons during coronal mass ejections, (This particular concept isn’t going to profit from them.) not likely of electrons.
2. We’re not talking incompressible fluids here. The electrons leaving the back side of the grid are going to have very little influence on those entering the front.
1. Everything in our Univers is moving, you cannot deny this fact, charched particles in interstellar vacuum too.
2. Mow you begin to invent the new limitation and postulate what motion direction is good for electron, what is bad :-)
If I could accept your argument about the time that electron will “spend” less time between electrodes, I could argument that “staying” between electrodes time depends also on intial speed vector of electron, it equally probable that electron will be becelerated between plates and as sequence will spend more time than proton :-)
3. More arguments I gave in my multiple comments on this topic, I’ve tired already, I see here is huge bias on this forum, that ready accept any idea of the peoples “from the pull”, and denying idea of any competitors.
IMHO , Summary proposed concept contains so much mistakes and wrong calcultation, so cannot be regarded seriously, joke.
Sorry misprint, In par.2 – I meant that depending on initial speed vector, electron can be decelerated between the grids , so will stay more time… – funny
You are exactly correct. As presented, no current is drawn from the power source, and no ions will be accelerated.
The possibility should be entertained that the entire spacecraft might get positively/negatively charged? If so, also what the consequences are.
The consequences would be truly shocking….but seriously, I think that could be easily prevented as a charged object would attract the counter charges it needs to remain net uncharged.
There are systems flying now that take care of the electric potential of spacecraft.
Quote by Patient Observer: ” like a solar sail but with the potential for considerably faster acceleration.” The slow acceleration and deceleration of this dipole drive is the main reason why I don’t think it will be able to compete with other faster technology considered by NASA to be a propulsion system for manned spacecraft. I don’t think that problem can be solved with the dipole drive.
Not on the vessel with crew no, but it would be very useful for rendezvous missions to the asteroid belt. Its unique ability to travel to any direction allows and return back to earth makes it a potential game changer
I’m impressed by how many people commenting on this particular article not only don’t understand the principles at work here, but are really militant about not understanding them. I suppose most articles at Centauri Dreams just don’t provide the opportunity for this sort of confusion.
Exotic (and even not-so-exotic) propulsion does seem to excite passions, both pro and con. That isn’t necessarily unhealthy even when not especially useful. The author could play a role in defusing the conflict by expanding on certain points, but he is not participating in the discussion.
The comments in this thread contain many instances of confirmation bias. The discussion presents an opportunity to question ‘principles at work’ which the article claims. The system does require a full simulation, and ‘there are too many things going on to derive the performance from pencil & paper analysis.’ An orbital test would be decisive, but other systems, such as the Em Drive and Cannae Drive, also contend for the same opportunity. Carefully-controlled ground based prototypes/simulations fully shielded from electromagnetic interference are required to find empirical answers.
Well, at least the Dipole drive function on well-understood physics, the Em Drive and Cannae Drive are not, they had to make it up.
This system does not require simulation.
The physics is clear: we have a static, conservative field, there is an electrostatic potential, and no charge coming in from infinity will magically gain energy going out. It is physically impossible.
A rookie mistake stemming from the fact that the infinite capacitor model does not have a uniform far field potential. In the model, the potential in front of the capacitor is higher than that behind. In a real craft, the potential goes to zero in any direction, and particles coming through do not receive net acceleration.
If you really want a propellantless Drive, an electron gun coupled with a grid that absorbs electrons from the plasma will do. You could probably rig up something for protons, too, for more significant trust. A proton conducting ceramic grid or something. You can get exhaust velocity all the way so to almost light speed, using basic accelerator technology, no problem! Except, of course, where is the power coming from? Power to thrust will be minuscule. About as useful as using a flashlight as a photon rocket.
Propellantless drives are highly overrated. They just shift the problem from propellant to power source, which does not make it a lot easier. The flashlight photon rocket IS a propellantless Drive, and it is the best physically possible without sucking up propellant from somewhere.
Ahem, that should have been “thrust to power” being minuscule, of course.
I hope that your “understand” does not mean an implicit faith.
It is true that few here understand the basic physics. Very few realize that the Dipole Drive is based on an inapplicable model, the infinite capacitor. It has no chance of working as described, and AlexT is one of the few who get that, although he appears to have trouble expressing it clearly.
It looks like the power requirements in the article are overstated. Electron flows through the screen consume no power – they only add drag – just as reflected ions consume no power. Only when a passing electron is captured by the positive screen or an electron is donated to a passing ion by the negative screen will power be consumed bringing the voltage drop across the screens back up to value. So the efficiency should be quite a bit higher than shown, a good thing.
Yes, and actually, as described, no ions or electrons are absorbed by the grid at all, and thus no current flows through the power source. So, the efficiency is actually infinite, a very good thing. Perpetual motion, finally achieved.
A Couloub of protons is = coulomb * mass of proton/ elementary charge = 0.01043968 mg, not 0.011 mg
I think we could further improve the engine if we inject additional ions in between the 2 electrified grids. That way we can generate more thrust when there is insufficient ions in the magnetosphere. This would be especially useful for we attempting to slow down the vessel. It would them become an effective dipole ion drive
This concept is fundamentally unsound, as many here have said or suspected. The basic mistake is relying on the “infinite capacitor” approximation. In reality, a proton will be decelerated before reaching the positive grid, exactly as much as it is accelerated afterwards.
More fundamentally, static electric fields are conservative, I.e. cannot impart net energy on a passing charge.
Another easy way to see something is very wrong is the fact that no mechanism is provided for charges to enter or exit the grids. No current, no power, it is that simple.
Eniac is right, of course. But you can pulse it. Protons come in when voltage amplitude is low, get accelerated when voltage amplitude is high, and leave when voltage amplitude is low. In this way the drive can still accelerate.
“May be you right, but till now none of comenters that know well physic could not explain how charged particle momentum is transferred to the dipole acceleration.
Yes proton’s momentum will be higher, so what ?”
The particle has and electric field. The grid has an electric field. When the two electric field interact momentum is transferred.
For example put two magnets on a table. Push one swards the other. If the polarity of the two magnets is the same the two magnets will move apart. Momentum was transferred between the two even though they were never in physical contact.
Electric field work the same way as magnetic fields.
Scientists a long time ago suspended to wires from the ceiling both were give an identical charge. The two wires were pushed apart. When the two wires given opposite charges they moved toward each other. In this experiment you can also measure the current flowing through the two wires. As long as the two wires don’t touch there is zero current flow.
In the dipole drive and and conventional ion thrusters there is no current flow as long as a proton or electron doesn’t touch the wires that make up the grids. Most protons or electrons will never though the grids. However a small number and that causes a small about of current to flow into the grids
“In the dipole drive and and conventional ion thrusters there is no current flow as long as a proton or electron doesn’t touch the wires that make up the grids”
Not true for conventional ion thrusters. The flow of ions out of the thruster is a current of one charge per ion. The dipole drive has no net current, because the ion comes in with the same charge it leaves with.
As I see it, it could work. Even though I am not a physicist ;-)
1. Thrust stationary
Lets assume only one hydrogen atom gets ionized into a proton and electron in the exact middle of the dipole drive. Drive is stationary.
When a proton and electro are charged they will shoot off in seperate directions under the same force. At that time there is a zero thrust (F=qE) because both proton and electron have equal and opposite charges.
However the acceleration and particle weight will differ allowing the electron to exit the field first (F=ma).
At that point there is still a field acting on only the proton providing the thrust as stated by Robert.
With a constant flow of protons and electrons there will always be protons that are unmatched (electron repelled out of the drive). Creating a constant thrust (only lead time when starting the drive).
2. Thrust moving
Let’s assume particles enter the front of the drive at speed (ship moving/headwind).
This means electrons are closer to the exit but they are still at speed. This means they require energy to stop their velocity, reverse velocity and then eject. The faster the ship goes the longer the electron will be in the drive causing counter thrust.
The proton on the other hand is already at speed and gets accelerated further creating thrust. The faster the ship goes the shorter the proton will need to pass through the drive.
Following this logic the faster the drive goes the less thrust the drive will generate. There might even be a maximum velocity based on proton/electron mass ratio.
Possible problem will most likely be electron buildup in front of the drive.
3. Light speed
Electron can only go light speed so this could cause thrust to decay at higher energy levels because the electron will take more time to leave the drive. OR Acceleration goes to 0 making the counter thrust 0? (F=ma)
Anyhow I like the idea of Robert and this should get some real attention by real physicists. Do the math and build it ;-)
This is a possible winner for moving comfortably within our solar system or keeping satellite orbits from decaying. Depending on performance.
I can see how this works if we approximate the thruster as a pair of parallel grids of infinite extent. In that case, there is no field outside. Incoming ions accelerate as they fall down the electric potential from the positive grid to the negative. But:
1) How exactly is power being consumed? No doubt the grids will tend to discharge over time, because they’ll attract particles bearing charges opposite their own. Keeping them charged will require power, but I don’t see how that power requirement is simply related to the jet power. In any event, it should be pretty low, if Jahunen’s electric sails are feasible.
2) A pair of grids of finite size will produce long-range electric fields. Far away (at distances many times the grids’ dimensions), the field will resemble that of an electric dipole. Ions being swept up by the thruster will climb from zero potential at infinity to a finite positive potential as approach the positive grid. Assuming they reach the grid, they’ll then fall down the potential to the negative grid to its potential, and then will start climbing back up to zero potential as the move downstream from the thruster. The foregoing ignores Debye shielding, but I believe the point that the ions begin and end at zero potential still applies. So how do the ions wind up with a net acceleration?
PS For a proton density of 1e6 cm^-3, I get a required grid radius of just 40 m rather than the 127 m calculated in the 2nd paragraph after the heading “The Dipole Drive in Planetary Orbit”. Could it be that a decimal point slipped in converting from ions per cc to ions per cubic meter? I hope so — because this would make dipole drive easier!