Building a Bussard ramjet isn’t easy, but the idea has a life of its own and continues to be discussed in the technical literature, in addition to its long history in science fiction. Peter Schattschneider, who explored the concept in Crafting the Bussard Ramjet last February, has just published an SF novel of his own called The EXODUS Incident (Springer, 2021), where the Bussard concept plays a key role. But given the huge technical problems of such a craft, can one ever be engineered? In this second part of his analysis, Dr. Schattschneider digs into the question of hydrogen harvesting and the magnetic fields the ramjet would demand. The little known work of John Ford Fishback offers a unique approach, one that the author has recently explored with Centauri Dreams regular A. A. Jackson in a paper for Acta Astronautica. The essay below explains Fishback’s ideas and the options they offer in the analysis of this extraordinary propulsion concept. The author is professor emeritus in solid state physics at Technische Universität Wien, but he has also worked for a private engineering company as well as the French CNRS, and has been director of the Vienna University Service Center for Electron Microscopy.
by Peter Schattschneider

As I mentioned in a recent contribution to Centauri Dreams, the BLC1 signal that flooded the press in January motivated me to check the science of a novel that I was finishing at the time – an interstellar expedition to Proxima Centauri on board a Bussard ramjet. Robert W. Bussard’s ingenious interstellar ramjet concept [1], published in 1960, inspired a generation of science fiction authors; the most celebrated is probably Poul Anderson with the novel Tau Zero [2]. The plot is supposedly based on an article by Carl Sagan [3] who references an early publication of Eugen Sänger where it is stated that due to time dilation and constant acceleration at 1 g „[…] the human lifespan would be sufficient to circumnavigate an entire static universe“ [4].
Bussard suggested using magnetic fields to scoop interstellar hydrogen as a fuel for a fusion reactor, but he did not discuss a particular field configuration. He left the supposedly simple problem to others as Newton did with the 3-body problem, or Fermat with his celebrated theorem. Humankind had to wait 225 years for an analytic solution of Newton‘s problem, and 350 years for Fermat’s. It took only 9 years for John Ford Fishback to propose a physically sound solution for the magnetic ramjet [5].
The paper is elusive and demanding. This might explain why adepts of interstellar flight are still discussing ramjets with who-knows-how-working superconducting coils that generate magnetic scoop fields reaching hundreds or thousands of kilometres out into space. Alas, it is much more technically complicated.
Fishback’s solution is amazingly simple. He starts from the well known fact that charged particles spiral along magnetic field lines. So, the task is to design a field the lines of which come together at the entrance of the fusion reactor. A magnetic dipole field as on Earth where all field lines focus on the poles would do the job. Indeed, the fast protons from the solar wind are guided towards the poles along the field lines, creating auroras. But they are trapped, bouncing between north and south, never reaching the magnetic poles. The reason is rather technical: Dipole fields change too rapidly along the path of a proton in order to keep it on track.
Fishback simply assumed a sufficiently slow field variation along the flight direction, Bz=B0/(1+ ? z) with a „very small“ ?. Everything else derives from there, in particular the parabolic shape of the magnetic field lines. Interestingly, throughout the text one looks in vain for field strengths, let alone a blueprint of the apparatus. The only hint to the visual appearance of the device is a drawing of a long, narrow paraboloid that would suck the protons into the fusion chamber. As a shortcut to what the author called the region dominated by the ramjet field I use here the term „Fishback solenoid“.
Fig. 1 is adapted from the original [5]. I added the coils that would create the appropriate field. Their distance along the axis indicates the decreasing current as the funnel widens. Protons come in from the right. Particles outside the scooping area As are rejected by the field. The mechanical support of the coils is indicated in blue. It constitutes a considerable portion of the ship’s mass, as we shall see below.

Fig. 1: Fishback solenoid with parabolic field lines. The current carrying coils are symbolized in red. The mechanical support is in blue. The strong fields exert hoop stress on the support that contributes considerably to the ship’s mass. Adapted from [5].
Searching for scientific publications that build upon Fishback’s proposal, Scopus renders 6 citations up to this date (April 2021). Some of them deal with the mechanical stress of the magnetic field, another aspect of Fishback’s paper that I discuss in the following, but as far as I could see the paraboloidal field was not studied in the 50 years since. This is surprising because normally authors continue research when they have a promising idea, and others jump on the subject, from which follow-up publications arise, but J. F. Fishback published only this one paper in his lifetime. [On Fishback and his tragic destiny, see John Ford Fishback and the Leonora Christine, by A. A. Jackson].
Solving the dynamic equation for protons in the Fishback field proves that the concept works. The particles are guided along the parabolic field lines toward the reactor as shown in the numerical simulation Fig. 2.
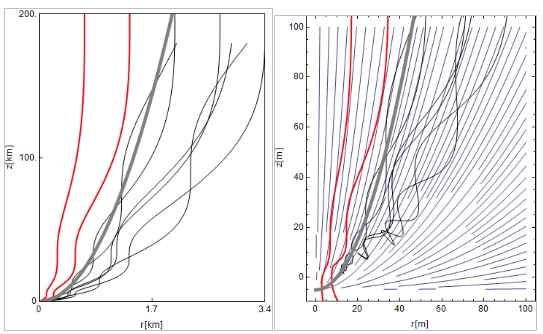
Fig.2: Proton paths in an (r,z)-diagram. r is the radial distance from the symmetry axis, z is the distance along this axis. The ship flies at 0.56 c (?=0.56) in positive z-direction. In the ship’s rest frame, protons arrive with a kinetic energy of 194 MeV from the top. Left: Protons entering the field at z=200 km are focussed to the reactor mouth at the coordinate origin, gyrating over the field lines. Particles following the red paths make it to the chamber; protons following the black lines spiral back. The thick grey parabola separates the two regimes. Right: Zoom into the first 100 m in front of the reactor mouth of radius 10 m. Magnetic field lines are drawn in blue.
The reactor intake is centered at (r,z)=(0,0). In the ship’s rest frame the protons arrive from top – here with 56 % of light speed, the maximum speed of the EXODUS in my novel [8]. Some example trajectories are drawn. Protons spiral down the magnetic field lines as is known from earth’s magnetic field and enter the fusion chamber (red lines). The scooping is well visible. The reactor mouth has an assumed radius of 10 m. A closer look into the first 100 m (right figure) reveals an interesting detail: Only the first two trajectories enter the reactor. Protons travelling beyond the bold grey line are reflected before they reach the entrance, just as charged particles are bouncing back in the earth’s field before they reach the poles. From the Figure it is evident that at an axial length of 200 km of the Fishback solenoid the scoop radius is disappointingly low – only 2 km. Nevertheless, the compression factor (focussing ions from this radius to 10 m) of 1:40.000 is quite remarkable.
The adiabatic condition mentioned above allows a simple expression for the area from which protons can be collected. The outer rim of this area is indicated by the thick grey line in Fig. 2. The supraconducting coils of the solenoid should ideally be built following this paraboloid, as sketched in Fig. 1. Tuning the ring current density to
![]()
yields a result that approximates Fishback‘s field closely.
What does it mean in technical terms? Let me discuss an idealized example, having in mind Poul Anderson’s novel. The starship Leonora Christina accelerates at 1 g, imposing artificial earth gravity on the crew. Let us assume that the ship‘s mass is a moderate 1100 tons (slightly less than 3 International Space Stations). For 1 g acceleration on board, we need a peak thrust of ~11 million Newton, about 1/3 of the first stage of the Saturn V rocket. The ship must be launched with fuel on stock because the ramjet operates only beyond a given speed, often taken as 42 km/s, the escape velocity from the solar system. In the beginning, the thrust is low. It increases with the ship’s speed because the proton throughput increases, asymptotically approaching the peak thrust.
Assuming complete conversion of fusion energy into thrust, total ionisation of hydrogen atoms, and neglecting drag from deviation of protons in the magnetic field, at an interstellar density of 106 protons/m3, the „fuel“ collected over one square kilometer yields a peak thrust of 1,05 Newton, a good number for order-of-magnitude estimates. That makes a scooping area of ~10 million square km, which corresponds to an entrance radius of about 1800 km of the Fishback solenoid. From Fig. 2, it is straightforward to extrapolate the bold grey parabola to the necessary length of the funnel – one ends up with fantastic 160 million km, more than the distance earth – sun. (At this point it is perhaps worth mentioning that this contribution is a physicist’s treatise and not that of an engineer.)
Plugging the scooping area into the relativistic rocket equation tells us which peak acceleration is possible. The results are summarised in Table 1. For convenience, speed is given in units of the light speed, ß=v/c. Additionally, the specific momentum ß? is given where
![]()
is the famous relativistic factor. (Note: The linear momentum of 1 kg of matter would be ß? c.) Acceleration is in units of the earth gravity acceleration, g=9.81 m/s2.
Under continuous acceleration such a starship would pass Proxima Centauri after 2.3 years, arrive at the galactic center after 11 years, and at the Andromeda galaxy after less than 16 years. Obviously, this is not earth time but the time elapsed for the crew who profit from time dilation. There is one problem: the absurdly long Fishback solenoid. Even going down to a scooping radius of 18 km, the supraconducting coils would reach out 16,000 km into flight direction. In this case the flight to our neighbour star would last almost 300 years.
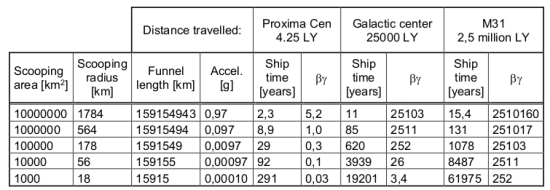
Table 1: Acceleration and travel time to Proxima Centauri, the galactic center, and the Andromeda galaxy M31, as a function of scooping area. ß? is the specific momentum at the given ship time. A ship mass of 1100 tons, reactor entrance radius 10 m, and constant acceleration from the start was assumed. During the starting phase the thrust is low, which increases the flight time by one to several years depending on the acceleration.
Fishback pointed out another problem of Bussard ramjets [5]. The magnetic field exerts strong outward Lorentz forces on the supraconducting coils. They must be balanced by some rigid support, otherwise the coils would break apart. When the ship gains speed, the magnetic field must be increased in order to keep the protons on track. Consequently, for any given mechanical support there is a cut-off speed beyond which the coils would break. For the Leonora Christina a coil support made of a high-strength „patented“ steel must have a mass of 1100 tons in order to sustain the magnetic forces that occur at ?=0,74.
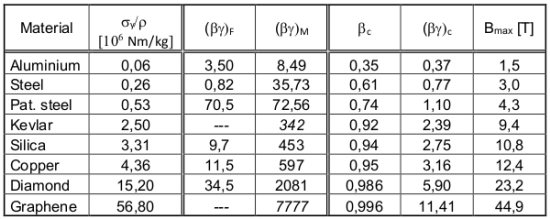
Table 2: Cut-off speeds ?c and cut-off specific momenta (ß?)c (upper bounds) for several support materials. (ß?)F from [5], (ß?)M from [7]. ?y/? is the ratio of the mechanical yield stress to the mass density of the support material. Bmax is the maximum magnetic field at the reactor entrance at cut-off speed. A scooping area of 10 million km2 was assumed, allowing a maximum acceleration of ~1 g for a ship of 1100 tons. Values in italics for Kevlar and graphene, unknown in the 1960s, were calculated based on equations given in [7].
But we assumed above that this is the ship‘s entire mass. That said, the acceleration must drop long before speeding at 0,74 c. The cut-off speed ?c=0,74 is an upper bound (for mathematicians: not necessarily the supremum) for the speed at which 1 g acceleration can be maintained. Lighter materials for the coil support would save mass. Fishback [5] calculated upper bounds for the speed at which an acceleration of 1 g is still possible for several materials such as aluminium or diamond (at that time the strongest lightweight material known). Values are shown in Table 2 together with (ß?)c.
Martin [7] found some numerical errors in [5]. Apart from that, Fishback used an optimistically biased (ß?)c. Closer scrutiny, in particular the use of a more realistic rocket equation [6], results in more realistic upper bounds. Using graphene, the strongest material known, the specific cut-off momentum is 11,41. This value would be achieved after a flight of three years at a distance of 10 light years. After that point, the acceleration would rapidly drop to values making it hopeless to reach the galatic center in a lifetime.
In conclusion, the interstellar magnetic ramjet has severe construction problems. Some future civilization may have the knowhow to construct fantastically long Fishback solenoids and to overcome the minimum mass condition. We should send a query to the guys who flashed the BLC1 signal from Proxima Centauri. The response is expected in 8.5 years at the earliest. In the meantime the educated reader may consult a tongue-in-cheek solution that can be found in my recent scientific novel [8].
Acknowledgements
Many thanks to Al Jackson for useful comments and for pointing out the source from which Poul Anderson got the idea for Tau Zero, and to Paul Gilster for referring me to the seminal paper of John Ford Fishback.
References
[1] Robert W. Bussard: Galactic Matter and Interstellar Flight. Astronautica Acta 6 (1960), 1-14.
[2] Poul Anderson: Tau Zero. Doubleday 1970.
[3] Carl Sagan: Direct contact among galactic civilizations by relativistic inter-stellar space flight, Planetary and Space Science 11 (1963) 485-498.
[4] Eugen Sänger: Zur Mechanik der Photonen-Strahlantriebe. Oldenbourg 1956.
[5] John F. Fishback: Relativistic Interstellar Space Flight. Astronautica Acta 15 (1969), 25-35.
[6] Claude Semay, Bernard Silvestre-Brac: The equation of motion of an interstellar Bussard ramjet. European Journal of Physics 26 (1) (2005) 75-83.
[7] Anthony R. Martin: Structural limitations on interstellar space flight. Astronautica Acta 16 (6) (1971) 353-357.
[8] Peter Schattschneider: The EXODUS Incident. Springer 2021,
ISBN: 978-3-030-70018-8. https://www.springer.com/de/book/9783030700188#aboutBook



My friend Dan Whitmire* showed the pp fusion reaction , for a 1 g ship, requires a reactor length of 1000 km ! He showed this could be reduced to 20 meters using the CNO cycle. Tho how one recycled Carbon for reuse is problematic. The reactors for the ram augmented and laser powered ramjets can be small enough but the ‘scoop’ , as Peter describes , because of its length and mass , now becomes a severe constraint. If advanced civilizations build ramjets they sure seem observable , but I would think they will solve the problem with more finesse, namely sails or less gigantic vehicles.
(Note the online version of Whitmire’s paper contains some copy mistakes.)
*D. P. Whitmire, Relativistic space
ight and the catalytic nuclear ramjet,
Acta Astronautica 2 (1975) 497{509.
The amount needed is very small and maybe we just don’t need to recycle it, the interstellar medium has small amounts of it already. We could have it onboard and fed into the reactor by say a forward facing accelerator to seed the scoop ahead as the craft moves through space. Incidently I was thinking to use the CNO cycle to remove venus’s atmosphere, if a ball hydrogen could impact the atmosphere at a fusion velocity an accelerated fusion reaction would remove a lot more atmosphere per buck of hydrogen used to impact it.
Funnelling down interstellar hydrogen into a minute volume is the proper direction towards achieving nuclear fusion. Is the ramjet plan in itself adequate to initiate and maintain fusion, or does fusion remain “twenty years in the future”?
Very, very interesting article ! Quite insightful, and I might even buy the book to read his take on this fictional treatment of interstellar travel.
Perhaps somebody out there can correct me if I’m wrong but I do recall reading somewhere that there is the unique capability of producing “anti-magnetic fields” which are essentially magnetic fields which can act to counter the stresses induced in the superconducting magnets with appropriate additional magnets that produce a counter magnetic stressor field. I, for the life of me cannot recall where or when I read that but I think it had something to do with the tremendous magnetic stress induced in the superconducting coils associated with the ITER fusion reactor currently under construction in the south of France.
I don’t believe these counter magnetics are being employed with the actual reactor being built in France, but I do recall that there was discussion in conjunction with the entire subject that you could construct a means to produce (with additional coils) fields which could permit materials to sustain (with what would be otherwise unsustainable) forces on a given material. Does anyone out there know about what I’m talking about or has heard about a similar situation ?
I do think that exist as a real possible solution to this problem, and I would even imagine that having a scoop such as propose that would be of length equal to the distance between the earth and the sun would be possible as a construction possibility. I can imagine there would be considerably other difficulties not even related to the construction but merely to the expected interactions with the interstellar medium.
The Plasma Magnet approach to magnetic sails works by inducing the charged medium to create a field. The size of the field expands inversely with the density of the medium. Is there any way this approach might be used to reduce the structure and mass of the scoop?
For more modest distances, ie interplanetary rather than interstellar flight, the scoop size could be reduced by increasing the density of the medium. In this case a particle beam. The scoop would be primarily in the tail of the ship to refocus the diverging charged protons and fuse them for thrust. This would be similar to laser-powered photon sails, except that the system accelerates particles to a high fraction of c, and rather than just transferring momentum, the craft would use fusion to create an even higher exhaust velocity than the incoming proton beam.
If the ramjet can use particles with incoming velocities greater than 42 km/s, then it should be able to work with the solar wind. A sun diver maneuver to accelerate towards the sun, and if the velocity at the perihelion was greater than around 450 km/s, the scoop would now capture the solar wind by overtaking it at the needed velocity and continuing to accelerate.
I had the idea many ‘moons’ ago to gather hydrogen and helium from the solar wind by using powerful magnetic field on the moon to bring water to there, it could be used to test the buzzard ramjet concept nearer home.
Alex, if we had two funnels side by side and at the base of the cones turned tightly by 90 degrees they would collide at twice the velocity improving fusion chances.
The ship would now look like the proverbial “ram”, but with the horns back to front. The ship’s scoops would be like those old 2-horn listening devices for aircraft when you put the ends of the horns in your ears. That 90 degree turn might need some serious power to prevent particle loss, although the scale of the scoops might mean a relatively gentle curvature.
The main problem I see with this approach is that the particles are now at rest relative to the ship’s direction. The hot plasma would therefore need to be more tightly contained. When the particles are just compressed but still traveling in the exhaust direction, they just need containment while the fusion is occurring and the fused particles accelerate away faster reducing the need to deflect/absorb the particles.
The size of the scoop mouths would imply that the exits would be quite far apart if the scoops were parallel, which implies more structural overhead compared to a single scoop. OTOH, the scoop mouths could each have 1/2 the area of a single scoop, making them smaller. With 2 scoops widely separated at the fusion end, the fusion chamber could be centered between the scoops, with the bulk of the ship’s mass could be split in 2 behind each scoop, rather like a catamaran design. The 2 hulls and scoops could slowly rotate to provide artificial gravity while the exhaust could be many kilometers away and well behind the ship for safety.
However, the engineering tradeoffs are way over my abilities to assess. But it might make for a novel sci-fi ship design.
In the news today: https://phys.org/news/2021-07-scientists-year-mystery-jupiter-x-ray.html Apparently Jupiter’s periodic X-ray aurorae are due to waves of plasma created by vibrations in the magnetosphere. They may not be generally suitable for a Bussard ramjet, but do you suppose such concentrations of ions might be used for experimenting with some aspects of ramjet design?
Perhaps we could use the helium component of the interstellar medium, if it could be deflected to the side it would act as a compression force reducing the tensile forces trying to rip it apart. It would act as a drag force though but may give more benefits than negatives.
Would a physical cone of charged graphene be better to shallow angle deflect hydrogen and helium into the engine with a much smaller magnetic field near the engine mouth. Graphene would be strong enough to deflect relativistic hydrogen and helium at shallow angles without damaging it. Napkin mass of a 200 km diameter cone is around 100 to 150 tons.
It would appear a cone of graphene to deflect the hydrogen and helium would be better than a magnetic field alone. I recalculated to get a mass of 26 tons for a single layer graphene cone of 200 km throat diameter and 200 km in length. The force of the incoming matter would want to collapse it but an electrostatic charge could keep it rigid.
Is there any chance the ‘scoop field’ can be made cyclically variable, in such a way as to create an active compressing mechanism using field variations? ‘Swallow’ the plasma? Maybe a rotating, spiral (helix) shaped field variation that ‘presses’ the plasma backwards towards the reactor, or ‘swallow’ more like the way a squid propels itself? In that case, we would not talk about a pure ramjet, as the ‘ram’ would be of an assisted nature.
I would think a pulse reactor would be an idea, i.e. choke the plasma with a magnetic pinch until fusion is reached and then let it go out the exhaust and repeat. Perhaps we could have a graphene cone with a circulating current rotated to a high velocity which could amplify the magnetic field.
Regarding ISM proton density.
The article assumes a density of 10^6 protons m^-3. (1 cm^-3). However, this ISM is made up of neutral gas as well as protons that combined make up the density. What are the implications if the density of protons is somewhat lower?
By contrast, the solar wind has a proton density 7x greater at 1 AU, and obviously much higher the closer to the sun.
At Venus, it is 14x greater, at Mercury 46x greater, and at the minimum approach to the sun of the Parker solar probe, 3300x greater.
This far higher density inside the solar system might be exploitable to reduce the could size and mass, if the various distances involved are great enough to allow the vehicle to reach the required velocities.
As Mike Serfas notes, the proton flux at Jupiter (Europa) is very high, and it might be possible to target Jupiter to make use of that proton source as the ship accelerates away from the sun.
Taken together, what velocities might a Bussard Ramjet accomplish within the solar system using the solar wind and Jupiter proton fluxes?
Lastly, in my previous comment I suggested using a particle beam to create the high particle densities to reduce the scoop mass. Given the high particle density of the solar wind close to the sun, would it be make sense to collimate a beam of particles at that location and send that beam to the ship? I envisage a scoop near the sun, concentrating the solar wind and send that concentrated beam towards the ship’s scoop. Despite the divergence, such a beam would allow for a longer acceleration path within a high density proton flux. The ship’s mass would be correspondingly lower and allow for a higher acceleration. In addition, the drag effects would be much lower as the solar wind density forward of the ship would be low in comparison, and the scoop would not be operating in the ISM. The scoop might be converted into a magsail to help decelerate the ship at its target.
Phys.org had an article about wood like steel recently.
My bootstrapping approach might be to have a more conventional mission to find whatever it was that passed through our planet in 1993 that SMU detected as a linear earthquake…and coax that into being a star drive of some kind. That might help along a ramjet/rairjet
The epilinear event detected from Australia and South america?
Yes it was an odd event that spurred speculation on the passage of quarkonium, a miniature black hole or perhaps a magnetic monopole.
Even odder… The Great Daylight Fireball of 1972 is thought to have made a 1,500 km aerobrake such that it was due to make a resonant return in the 1990s. Has anyone thought to match the trajectories of these two bodies? Vela too perhaps?
Oh there’s nothing odd about those! We had one also, some years before the 1972 one seen in the US. 1968-69? The estimates at the time was a quite larger asteroid around 200 meters in size, but today we know one such need not be more than 10 – 20 meters to create quite a spectacular show. The one here left a trail also.
13 October 1990 did bring another, now the estimate for such objects have been adjusted down, and thought to be 44 kilos.
Then again in 2020 Germany linked below, and in 2021 Sweden.
https://images.twnmm.com/c55i45ef3o2a/1SuG1PtrSJccBMpH4dlrHX/374438df6bebdea3edba1be342b6469a/Earthskimmer-Meteoroid-Germany-Sept22-2020-GMN.jpg
The Great Daylight Fireball (or US19720810) was an Earth-grazing fireball that passed within 57 kilometres (35 mi; 187,000 ft) of Earth’s surface at 20:29 UTC on August 10, 1972. It entered Earth’s atmosphere at a speed of 15 kilometres per second (9.3 mi/s)[2] in daylight over Utah, United States (14:30 local time) and passed northwards leaving the atmosphere over Alberta, Canada. It was seen by many people and recorded on film and by space-borne sensors.[3] An eyewitness to the event, located in Missoula, Montana, saw the object pass directly overhead and heard a double sonic boom. The smoke trail lingered in the atmosphere for several minutes.
The atmospheric pass modified the object’s mass and orbit around the Sun, but it is probably still in an Earth-crossing orbit and is thought to have passed close to Earth again in August 1997.[3] However IAU’s website states that these “suggestions have not been substantiated”
Analysis of its appearance and trajectory showed the object was about 3–14 m (10–45 ft) in diameter, depending on whether it was a comet made of ice or a stony and therefore denser asteroid.[2][5] Other sources identified it as an Apollo asteroid in an Earth-crossing orbit that would make a subsequent close approach to Earth in August 1997.[3] In 1994, Czech astronomer Zden?k Ceplecha reanalysed the data and suggested the passage would have reduced the asteroid’s mass to about a third or half of its original mass (reducing its diameter to 2–10 metres (6.6–32.8 ft)).[5]
The object was tracked by military surveillance systems and sufficient data obtained to determine its orbit both before and after its 100-second passage through Earth’s atmosphere. Its velocity was reduced by about 800 metres per second (2,600 ft/s) and the encounter significantly changed its orbital inclination from 15 degrees to 7 degrees
Since we are entertaining structures hundreds of km long, why not combine a shorter funnel of current hoops with a very long and thin anode ‘antenna’ projecting in front of the scoop to concentrate ions in front of its path? The resulting structure would be simpler to build and less massive.
(——————- +
It would repel some ions too?
This is all very interesting, if a touch “aspirational”, but what I wonder is what will we do with the protons after they’ve been collected and mildly accelerated. Until we achieve controlled fusion we do not need the fuel. Only once we know how to do that will we be in a position to determine what the collection and “processing” need to accomplish. What we’re doing is designing a carburetor without having any idea how to build an internal combustion engine and having a limited conception of the atmosphere’s content and state.
Slightly OT if we did have a large magnetic scoop on the moon collecting hydrogen and helium from the SW say the size of the moons diameter it would collect thousands of tons of water equivalent per year. Not only that tens of kilograms of helium 3 and generate a few gigawatts of power from the mass collected as it is funneled in. If the hydrogen is fused to make power it is multiples of that. Mercury would be even bigger than that.
Oh too dream !