We’ve spoken recently about civilizations expanding throughout the galaxy in a matter of hundreds of thousands of years, a thought that led Frank Tipler to doubt the existence of extraterrestrials, given the lack of evidence of such expansion. But let’s turn the issue around. What would the very beginning of our own interstellar exploration look like, if we reach the point where probes are feasible and economically viable? This is the question Johannes Lebert examines today. Johannes obtained his Master’s degree in Aerospace at the Technische Universität München (TUM) this summer. He likewise did his Bachelor’s in Mechanical Engineering at TUM and was visiting student in the field of Aerospace Engineering at the Universitat Politècnica de València (UPV), Spain. He has worked at Starburst Aerospace (a global aerospace & defense startup accelerator and strategic advisory company) and AMDC GmbH (a consultancy with focus on defense located in Munich). Today’s essay is based upon his Master thesis “Optimal Strategies for Exploring Nearby-Stars,” which was supervised by Martin Dziura (Institute of Astronautics, TUM) and Andreas Hein (Initiative for Interstellar Studies).
by Johannes Lebert
1. Introduction

Last year, when everything was shut down and people were advised to stay at home instead of going out or traveling, I ignored those recommendations by dedicating my master thesis to the topic of interstellar travel. More precisely, I tried to derive optimal strategies for exploring near-by stars. As a very early-stage researcher I was really honored when Paul asked me to contribute to Centauri Dreams and want to thank him for this opportunity to share my thoughts on planning interstellar exploration from a strategic perspective.

Figure 1: Me, last year (symbolic image). Credit: hippopx.com).
As you are an experienced and interested reader of Centauri Dreams, I think it is not necessary to make you aware of the challenges and fascination of interstellar travel and exploration. I am sure you’ve already heard a lot about interstellar probe concepts, from gram-scale nanoprobes such as Breakthrough Starshot to huge spaceships like Project Icarus. Probably you are also familiar with suitable propulsion technologies, be it solar sails or fusion-based engines. I guess, you could also name at least a handful of promising exploration targets off the cuff, perhaps with focus on star systems that are known to host exoplanets. But have you ever thought of ways to bring everything together by finding optimal strategies for interstellar exploration? As a concrete example, what could be the advantages of deploying a fleet of small probes vs. launching only few probes with respect to the exploration targets? And, more fundamentally, what method can be used to find answers to this question?
In particular the last question has been the main driver for this article: Before starting with writing, I was wondering a lot what could be the most exciting result I could present to you and found that the methodology as such is the most valuable contribution on the way towards interstellar exploration: Once the idea is understood, you are equipped with all relevant tools to generate your own results and answer similar questions. That is why I decided to present you a summary of my work here, addressing more directly the original idea of Centauri Dreams (“Planning […] Interstellar Exploration”), instead of picking a single result.
Below you’ll find an overview of this article’s structure to give you an impression of what to expect. Of course, there is no time to go into detail for each step, but I hope it’s enough to make you familiar with the basic components and concepts.
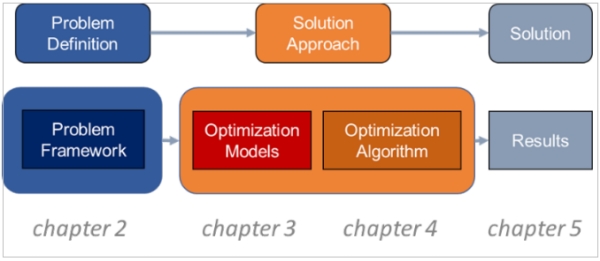
Figure 2: Article content and chapters
I’ll start from scratch by defining interstellar exploration as an optimization problem (chapter 2). Then, we’ll set up a model of the solar neighborhood and specify probe and mission parameters (chapter 3), before selecting a suitable optimization algorithm (chapter 4). Finally, we apply the algorithm to our problem and analyze the results (more generally in chapter 5, with implications for planning interstellar exploration in chapter 6).
But let’s start from the real beginning.
2. Defining and Classifying the Problem of Interstellar Exploration
We’ll start by stating our goal: We want to explore stars. Actually, it is star systems, because typically we are more interested in the planets that are potentially hosted by a star instead of the star as such. From a more abstract perspective, we can look at the stars (or star systems) as a set of destinations that can be visited and explored. As we said before, in most cases we are interested in planets orbiting the target star, even more if they might be habitable. Hence, there are star systems which are more interesting to visit (e. g. those with a high probability of hosting habitable planets) and others, which are less attracting. Based on these considerations, we can assign each star system an “earnable profit” or “stellar score” from 0 to 1. The value 0 refers to the most boring star systems (though I am not sure if there are any boring star systems out there, so maybe it’s better to say “least fascinating”) and 1 to the most fascinating ones. The scoring can be adjusted depending on one’s preferences, of course, and extended by additional considerations and requirements. However, to keep it simple, let’s assume for now that each star system provides a score of 1, hence we don’t distinguish between different star systems. Having this in mind, we can draw a sketch of our problem as shown in Figure 3.
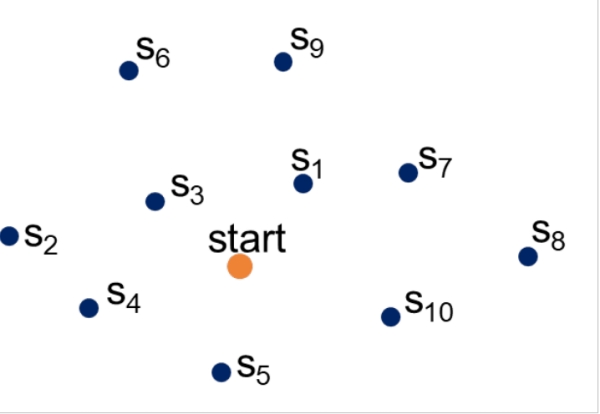
Figure 3: Solar system (orange dot) as starting point, possible star systems for exploration (destinations with score ) represented by blue dots
To earn the profit by visiting and exploring those destinations, we can deploy a fleet of space probes, which are launched simultaneously from Earth. However, as there are many stars to be explored and we can only launch a limited number of probes, one needs to decide which stars to include and which ones to skip – otherwise, mission timeframes will explode. This decision will be based on two criteria: Mission return and mission duration. The mission return is simply the sum of the stellar score of each visited star. As we assume a stellar score of 1 for each star, the mission return is equal to the number of stars that is visited by all our probes. The mission duration is the time needed to finish the exploration mission.
In case we deploy several probes, which carry out the exploration mission simultaneously, the mission is assumed to be finished when the last probe reaches the last star on its route – even if other probes have finished their route earlier. Hence, the mission duration is equal to the travel time of the probe with the longest trip. Note that the probes do not need to return to the solar system after finishing their route, as they are assumed to send the data gained during exploration immediately back to Earth.
Based on these considerations we can classify our problem as a bi-objective multi-vehicle open routing problem with profits. Admittedly quite a cumbersome term, but it contains all relevant information:
- Bi-objective: There are two objectives, mission return and mission duration. Note that we want to maximize the return while keeping the duration minimal. Hence, from intuition we can expect that both objectives are competing: The more time, the more stars can be visited.
- Multi-vehicle: Not only one, but several probes are used for simultaneous exploration.
- Open: Probes are free to choose where to end their route and are not forced to return back to Earth after finishing their exploration mission.
- Routing problem with profits: We consider the stars as a set of destinations with each providing a certain score si. From this set, we need to select several subsets, which are arranged as routes and assigned to different probes (see Figure 4).
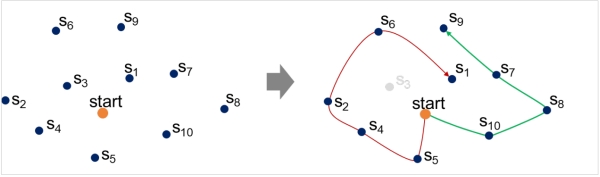
Figure 4: Problem illustration: Identify subsets of possible destinations si, find the best sequences and assign them to probes
Even though it appears a bit stiff, the classification of our problem is very useful to identify suitable solution methods: Before, we were talking about the problem of optimizing interstellar exploration, which is quite unknown territory with limited research. Now, thanks to our abstraction, we are facing a so-called Routing Problem, which is a well-known optimization problem class, with several applications across various fields and therefore being exhaustively investigated. As a result, we now have access to a large pool of established algorithms, which have already been tested successfully against these kinds of problems or other very similar or related problems such as the Traveling Salesman Problem (probably the most popular one) or the Team Orienteering Problem (subclass of the Routing Problem).
3. Model of the Solar Neighborhood and Assumptions on Probe & Mission Architecture
Obviously, we’ll also need some kind of galactic model of our region of interest, which provides us with the relevant star characteristics and, most importantly, the star positions. There are plenty of star catalogues with different focus and historical background (e.g. Hipparcos, Tycho, RECONS). One of the latest, still ongoing surveys is the Gaia Mission, whose observations are incorporated in the Gaia Archive, which is currently considered to be the most complete and accurate star database.
However, the Gaia Archive – more precisely the Gaia Data Release 2 (DR2), which will be used here* (accessible online [1] together with Gaia based distance estimations by Bailer-Jones et al. [2]) – provides only raw observation data, which include some reported spurious results. For instance, it lists more than 50 stars closer than Proxima Centauri, which would be quite a surprise to all the astronomers out there.
*1. Note that there is already an updated Data Release (Gaia DR3), which was not available yet at the time of the thesis.
Hence, a filtering is required to obtain a clean data set. The filtering procedure applied here, which consists of several steps, is illustrated in Figure 5 and follows the suggestions from Lindegren et al. [3]. For instance, data entries are eliminated based on parallax errors and uncertainties in BP and RP fluxes. The resulting model (after filtering) includes 10,000 stars and represents a spherical domain with a radius of roughly 110 light years around the solar system.
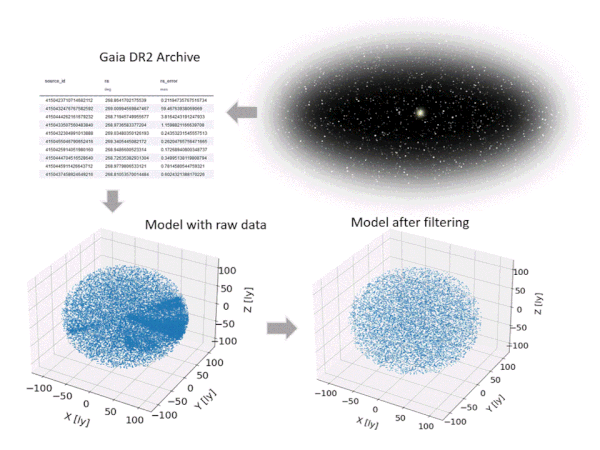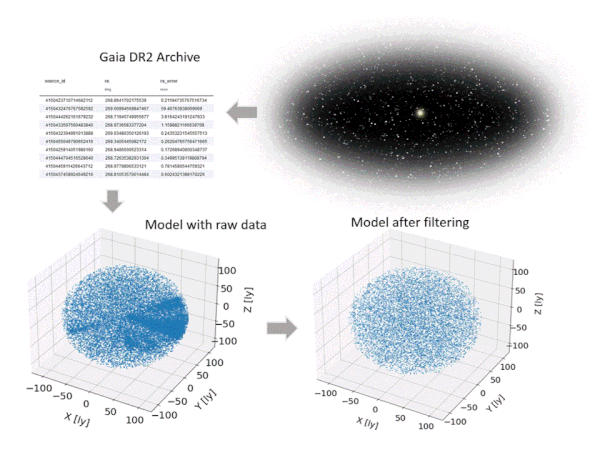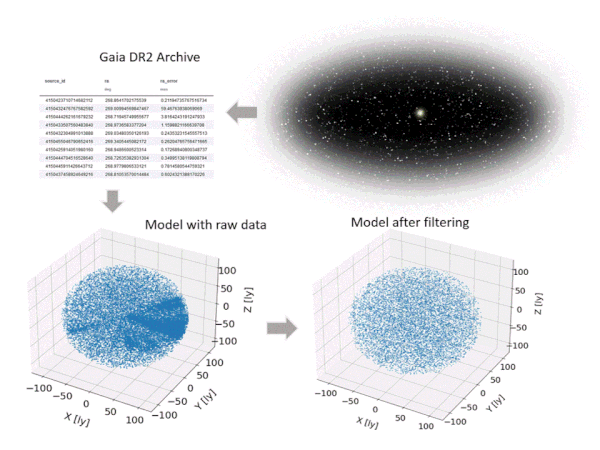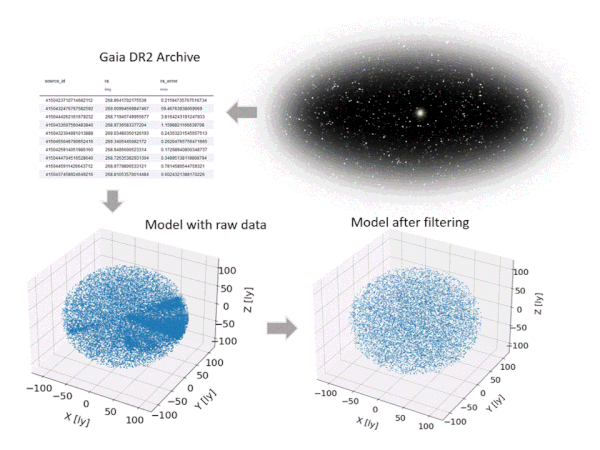
Figure 5: Setting up the star model based on Gaia DR2 and filtering (animated figure from [9])
To reduce the complexity of the model, we assume all stars to maintain fixed positions – which is of course not true (see Figure 5 upper right) but can be shown to be a valid simplification for our purposes, and we limit the mission time frames to 7,000 years. 7,000 years? Yes, unfortunately, the enormous stellar distances, which are probably the biggest challenge we encounter when planning interstellar travel, result in very high travel times – even if we are optimistic concerning the travel speed of our probes, which are defined by the following.
We’ll use a rather simplistic probe model based on literature suggestions, which has the advantage that the results are valid across a large range of probe concepts. We assume the probes to travel along straight-line trajectories (in line with Fantino & Casotto [4] at an average velocity of 10 % of the speed of light (in line with Bjørk [5]. They are not capable of self-replicating; hence, the probe number remains constant during a mission. Furthermore, the probes are restricted to performing flybys instead of rendezvous, which limits the scientific return of the mission but is still good enough to detect planets (as reported by Crawford [6]. Hence, the considered mission can be interpreted as a reconnaissance or scouting mission, which serves to identify suitable targets for a follow-up mission, which then will include rendezvous and deorbiting for further, more sophisticated exploration.
Disclaimer: I am well aware of the weaknesses of the probe and mission model, which does not allow for more advanced mission design (e. g. slingshot maneuvers) and assumes a very long-term operability of the probes, just to name two of them. However, to keep the model and results comprehensive, I tried to derive the minimum set of parameters which is required to describe interstellar exploration as an optimization problem. Any extensions of the model, such as a probe failure probability or deorbiting maneuvers (which could increase the scientific return tremendously), are left to further research.
4. Optimization Method
Having modeled the solar neighborhood and defined an admittedly rather simplistic probe and mission model, we finally need to select a suitable algorithm for solving our problem, or, in other words, to suggest “good” exploration missions (good means optimal with respect to both our objectives). In fact, the algorithm has the sole task of assigning each probe the best star sequences (so-called decision variables). But which algorithm could be a good choice?
Optimization or, more generally, operations research is a huge research field which has spawned countless more or less sophisticated solution approaches and algorithms over the years. However, there is no optimization method (not yet) which works perfectly for all problems (“no free lunch theorem”) – which is probably the main reason why there are so many different algorithms out there. To navigate through this jungle, it helps to recall our problem class and focus on the algorithms which are used to solve equal or similar problems. Starting from there, we can further exclude some methods a priori by means of a first analysis of our problem structure: Considering n stars, there are ?! possibilities to arrange them into one route, which can be quite a lot (just to give you a number: for n=50 we obtain 50!? 1064 possibilities).
Given that our model contains up to 10,000 stars, we cannot simply try out each possibility and take the best one (so called enumeration method). Instead, we need to find another approach, which is more suitable for those kinds of problems with a very large search space, as an operations researcher would say. Maybe you already have heard about (meta-)heuristics, which allow for more time-efficient solving but do not guarantee to find the true optimum. Even if you’ve never heard about them, I am sure that you know at least one representative of a metaheuristic-based solution, as it is sitting in front of your screen right now as you are reading this article… Indeed, each of us is the result of a thousands of years lasting, still ongoing optimization procedure called evolution. Wouldn’t it be cool if we could adopt the mechanisms that brought us here to do the next, big step in mankind and find ways to leave the solar system and explore unknown star systems?
Those kinds of algorithms, which try to imitate the process of natural evolution, are referred to as Genetic Algorithms. Maybe you remember the biology classes at school, where you learned about chromosomes, genes and how they are shared between parents and their children. We’ll use the same concept and also the wording here, which is why we need to encode our optimization problem (illustrated in Figure 6): One single chromosome will represent one exploration mission and as such one possible solution for our optimization problem. The genes of the chromosome are equivalent to the probes. And the gene sequences embody the star sequences, which in turn define the travel routes of each probe.
If we are talking about a set of chromosomes, we will use the term “population”, therefore sometimes one chromosome is referred to as individual. Furthermore, as the population will evolve over the time, we will speak about different generations (just like for us humans).
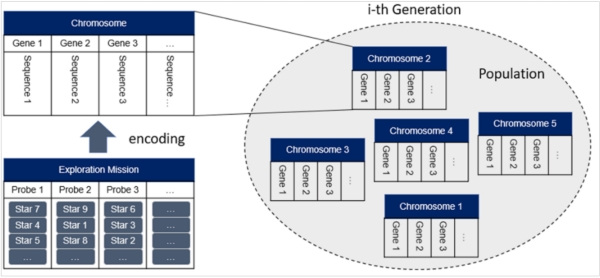
Figure 6. Genetic encoding of the problem: Chromosomes embody exploration missions; genes represent probes and gene sequences are equivalent to star sequences.
The algorithm as such is pretty much straightforward, the basic working principle of the Genetic Algorithm is illustrated below (Figure 7). Starting from a randomly created initial population, we enter an evolution loop, which stops either when a maximum number of generations is reached (one loop represents one generation) or if the population stops evolving and keeps stable (convergence is reached).
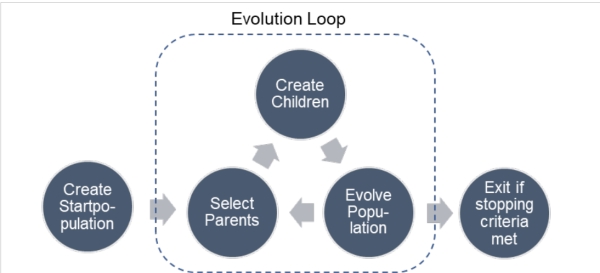
Figure 7: High level working procedure of the Genetic Algorithm
I don’t want to go into too much detail on the procedure – interested readers are encouraged to go through my thesis [7] and look for the corresponding chapter or see relevant papers (particularly Bederina and Hifi [8], from where I took most of the algorithm concept). To summarize the idea: Just like in real life, chromosomes are grouped into pairs (parents) and create children (representing new exploration missions) by sharing their best genes (which are routes in our case). For higher variety, a mutation procedure is applied to a few children, such as a partial swap of different route segments. Finally, the worst chromosomes are eliminated (evolve population = “survival of the fittest”) to keep the population size constant.
Side note: Currently, we have the chance to observe this optimization procedure when looking at the Coronavirus. It started almost two years ago with the alpha version; right now the population is dominated by the delta version, with omicron an emerging variant. From the virus perspective, it has improved over time through replication and mutation, which is supported by large populations (i.e., a high number of cases).
Note that the genetic algorithm is extended by a so-called local search, which comprises a set of methods to improve routes locally (e. g. by inverting segments or swapping two random stars within one route). That is why this method is referred to as Hybrid Genetic Algorithm.
Now let’s see how the algorithm is operating when applied to our problem. In the animated figure below, we can observe the ongoing optimization procedure. Each individual is evaluated “live” with respect to our objectives (mission return and duration). The result is plotted in a chart, where one dot refers to one individual and thus represents one possible exploration mission. The color indicates the corresponding generation.
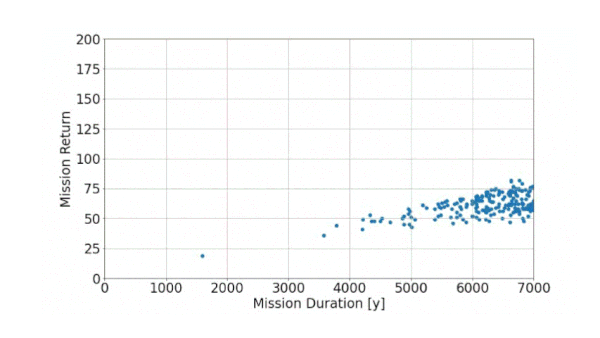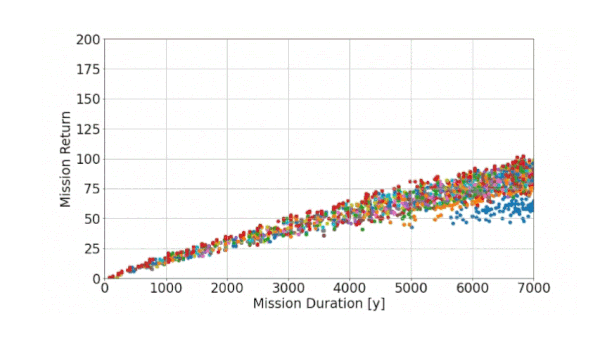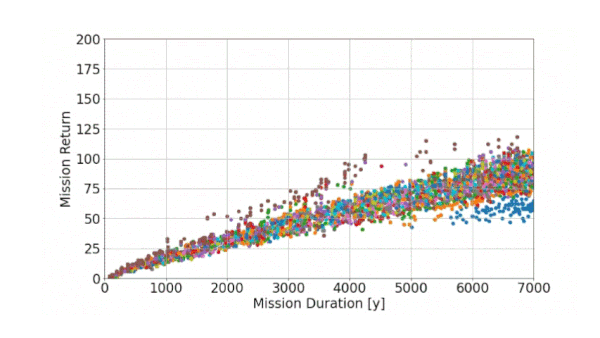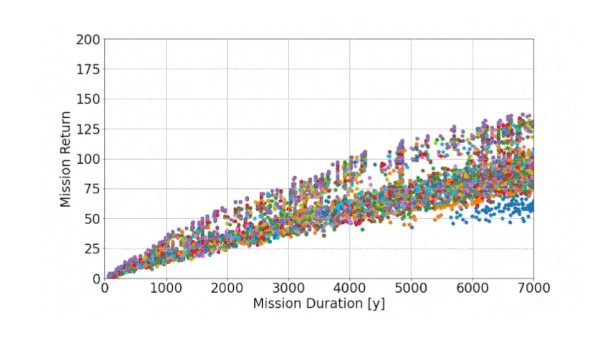
Figure 8: Animation of the ongoing optimization procedure: Each individual (represented by a dot) is evaluated with respect to the objectives, one color indicates one generation
As shown in this animated figure, the algorithm seems to work properly: With increasing generations, it tries to generate better solutions, as it optimizes towards higher mission return and lower mission duration (towards the upper left in the Figure 8). Solutions from the earlier generation with poor quality are subsequently replaced by better individuals.
5. Optimization Results
As a result of the optimization, we obtain a set of solutions (representing the surviving individuals from the final generation), which build a curve when evaluated with respect to our twin objectives of mission duration and return (see Figure 9). Obviously, we’ll get different curves when we change the probe number m between two optimization runs. In total, 9 optimization runs are performed; after each run the probe number is doubled, starting with m=2. As already in the animated Figure 8, one dot represents one chromosome and thus one possible exploration mission (one mission is illustrated as an example).
Figure 9: Resulting solutions for different probe numbers and mission example represented by one dot
Already from this plot, we can make some first observations: The mission return (which we assume equal to the number of explored stars, just as a reminder) increases with mission duration. More precisely, there appears to be an approximately linear incline of star number with time, at least in most instances. This means that when doubling the mission duration, we can expect more or less twice the mission return. An exception to this behavior is the 512 probes curve, which flattens when reaching > 8,000 stars due to the model limits: In this region, only few unexplored stars are left which may require unfavorable transfers.
Furthermore, we see that for a given mission duration the number of explored stars can be increased by launching more probes, which is not surprising. We will elaborate a bit more on the impact of the probe number and on how it is linked with the mission return in a minute.
For now, let’s keep this in our mind and take a closer look at the missions suggested by the algorithm. In the figure below (Figure 10), routes for two missions with different probe number m but similar mission return J1 (nearly 300 explored stars) are visualized (x, y, z-axes dimensions in light years). One color indicates one route that is assigned to one probe.
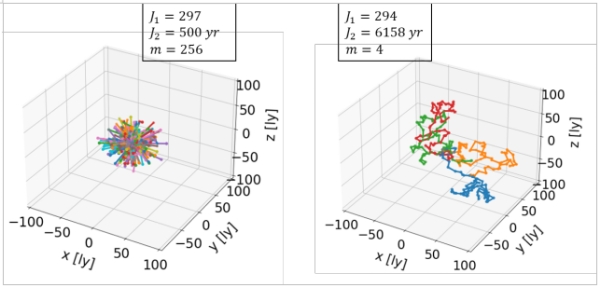
Figure 10: Visualization of two selected exploration missions with similar mission return J1 but different probe number m – left: 256 available probes, right: 4 available probes (J2 is the mission duration in years)
Even though the mission return is similar, the route structures are very different: The higher probe number mission (left in Figure 10) is built mainly from very dense single-target routes and thus focuses more on the immediate solar neighborhood. The mission with only 4 probes (right in Figure 10), contrarily, contains more distant stars, as it consists of comparatively long, chain-like routes with several targets included. This is quite intuitive: While for the right case (few probes available) mission return is added by “hopping” from star to star, in the left case (many probes available) simply another probe is launched from Earth. Needless to say, the overall mission duration J2 is significantly higher when we launch only 4 probes (> 6000 years compared to 500 years).
Now let’s look a bit closer at the corresponding transfers. As before, we’ll pick two solutions with different probe number (4 and 64 probes) and similar mission return (about 230 explored stars). But now, we’ll analyze the individual transfer distances along the routes instead of simply visualizing the routes. This is done by means of a histogram (shown in Figure 11), where simply the number of transfers with a certain distance is counted.
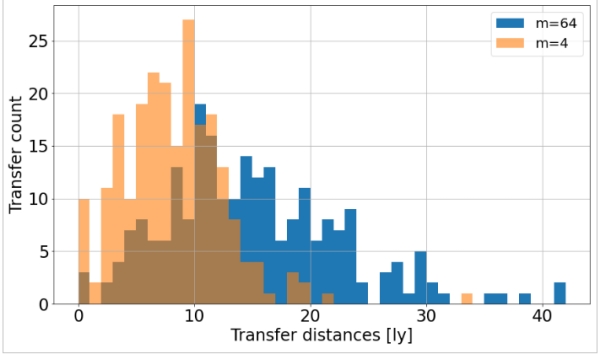
Figure 11: Histogram with transfer distances for two different solution – orange bars belong to a solution with 4 probes, blue bars to a solution with 64 probes; both provide a mission return of roughly 230 explored stars.
The orange bars belong to a solution with 4 probes, the blue ones to a solution with 64 probes. To give an example on how to read the histogram: We can say that the solution with 4 probes includes 27 transfers with a distance of 9 light years, while the solution with 64 probes contains only 8 transfers of this distance. What we should take from this figure is that with higher probe numbers apparently more distant transfers are required to provide the same mission return.
Based on this result we can now concretize earlier observations regarding the probe number impact: From Figure 9 we already found that the mission return increases with probe number, without being more specific. Now, we discovered that the efficiency of the exploration mission w. r. t. routing decreases with increasing probe number, as there are more distant transfers required. We can even quantify this effect: After doing some further analysis on the result curve and a bit of math, we’ll find that the mission return J1 scales with probe number m according to ~m0.6 (at least in most instances). By incorporating the observations on linearity between mission return and duration (J2), we obtain the following relation: J1 ~ J2m0.6.
As J1 grows only with m0.6 (remember that m1 indicates linear growth), the mission return for a given mission duration does not simply double when we launch twice as many probes. Instead, it’s less; moreover, it depends on the current probe number – in fact, the contribution of additional probes to the overall mission return diminishes with increasing probe numbers.
This phenomenon is similar to the concept of diminishing returns in economics, which denotes the effect that an increase of the input yields progressively lower or even reduced increase in output. How does that fit with earlier observations, e. g. on route structure? Apparently, we are running into some kind of a crowding effect, when we launch many probes from the same spot (namely our solar system): Long initial transfers are required to assign each probe an unexplored star. Obviously, this effect intensifies with each additional probe being launched.
6. Conclusions and Implications for Planning Interstellar Exploration
What can we take from all this effort and the results of the optimization? First, let’s recap the methodology and tools which we developed for planning interstellar exploration (see Figure 12).
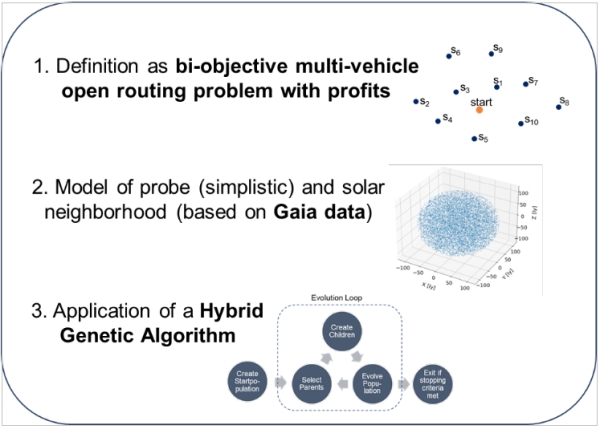
Figure 12: Methodology – main steps
Beside the methodology, which of course can be extended and adapted, we can give some recommendations for interstellar mission design considerations, in particular regarding the probe number impact:
- High probe numbers are favorable when we want to explore many stars in the immediate solar neighborhood. As further advantage of high probe numbers, mostly single-target missions are performed, which allows the customization of each probe according to its target star (e. g. regarding scientific instrumentation).
- If the number of available probes is limited (e. g. due to high production costs), it is recommended to include more distant stars, as it enables a more efficient routing. The aspect of higher routing efficiency needs to be considered in particular when fuel costs are relevant (i. e. when fuel needs to be transported aboard). For other, remotely propelled concepts (such as laser driven probes, e. g. Breakthrough Starshot) this issue is less relevant, which is why those concepts could be deployed in larger numbers, allowing for shorter overall mission duration at the expense of more distant transfers.
- When planning to launch a high number of probes from Earth, however, one should be aware of crowding effects. This effect sets in already for few probes and intensifies with each additional probe. One option to encounter this issue and thus support a more efficient probe deployment could be swarm-based concepts, as indicated by the sketch in Figure 13.
The swarm-based concept includes a mother ship, which transports a fleet of smaller explorer probes to a more distant star. After arrival, the probes are released and start their actual exploration mission. As a result, the very dense, crowded route structures, which are obtained when many probes are launched from the same spot (see again Figure 10, left plot), are broken up.
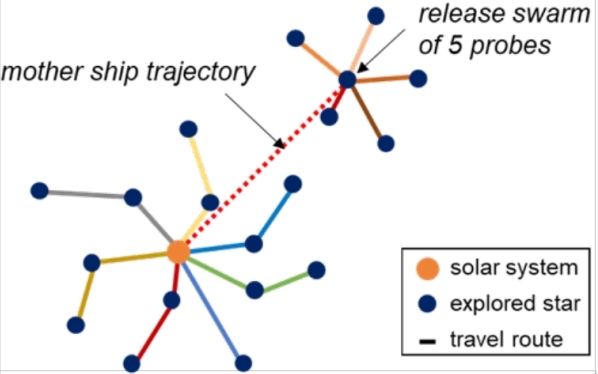
Figure 13: Sketch illustrating the beneficial effect of swarm concepts for high probe numbers.
Obviously, the results and derived implications for interstellar exploration are not mind-blowing, as they are mostly in line with what one would expect. However, this in turn indicates that our methodology seems to work properly, which of course does not serve as a full verification but is at least a small hint. A more reliable verification result can be obtained by setting up a test problem with known optimum (which is not shown here, but was also done for this approach, showing that the algorithm’s results deviate about 10% compared to the ideal solution).
Given the very early-stage level of this work, there is still a lot of potential for further research and refinement of the simplistic models. Just to pick one example: As a next step, one could start to distinguish between different star systems by varying the reward of each star system si based on a stellar metric, where more information of the star is incorporated (such as spectral class, metallicity, data quality, …). In the end it’s up to oneself, which questions he or she wants to answer – there is more than enough inspiration up there in the night sky.

Figure 14: More people, now
Assuming that you are not only an interested reader of Centauri Dreams but also familiar with other popular literature on that topic, you maybe have heard about Clarke’s three laws. I would like to close this article by taking up his second one: The only way of discovering the limits of the possible is to venture a little way past them into the impossible. As said before, I hope that the introduced methodology can help to answer further questions concerning interstellar exploration from a strategic perspective. The more we know, the better we are capable of planning and imagining interstellar exploration, thus pushing gradually the limits of what is considered to be possible today.
References
[1] ESA, “Gaia Archive,“ [Online]. Available: https://gea.esac.esa.int/archive/.
[2] C. A. L. Bailer-Jones et al., “Estimating Distances from Parallaxes IV: Distances to 1.33 Billion Stars in Gaia Data Release 2,” The Astronomical Journal, vol. 156, 2018.
https://iopscience.iop.org/article/10.3847/1538-3881/aacb21
[3] L. Lindegren et al., “Gaia Data Release 2 – The astrometric solution,” Astronomy & Astrophysics, vol. 616, 2018.
https://doi.org/10.1051/0004-6361/201832727
[4] E. Fantino and S. Casotto, “Study on Libration Points of the Sun and the Interstellar Medium for Interstellar Travel,” Universitá di Padova/ESA, 2004.
[5] R. Bjørk, “Exploring the Galaxy using space probes,” International Journal of Astrobiology, vol. 6, 2007.
https://doi.org/10.1017/S1473550407003709
[6] I. A. Crawford, “The Astronomical, Astrobiological and Planetary Science Case for Interstellar Spaceflight,” Journal of the British Interplanetary Society, vol. 62, 2009. https://arxiv.org/abs/1008.4893
[7] J. Lebert, “Optimal Strategies for Exploring Near-by Stars,“ Technische Universität München, 2021.
https://mediatum.ub.tum.de/1613180
[8] H. Bederina and M. Hifi, “A Hybrid Multi-Objective Evolutionary Algorithm for the Team Orienteering Problem,” 4th International Conference on Control, Decision and Information Technologies, Barcelona, 2017.
https://ieeexplore.ieee.org/document/8102710
[9] University of California – Berkeley, “New Map of Solar Neighborhood Reveals That Binary Stars Are All Around Us,” SciTech Daily, 22 February 2021.
https://scitechdaily.com/new-map-of-solar-neighborhood-reveals-that-binary-stars-are-all-around-us/



Without having to read your thesis, does the mission time J2 include the time for the data to return to Earth? Does the algorithm require exclusive visit by one probe to each star, or can more than one probe visit a star on a travel leg to the next star?
What this analysis suggests to me is that any civilization attempting any of these strategies has to be very stable. 250 years is a long time to maintain any objective program without abandoning it. 6000 years is about all of recorded history and about 1/2 the total of known civilization based on “city” building. Saturating the mission with probes gets the earliest returns but with a high economic cost. This suggests that for a science mission, this will only be undertaken when there are no national rivalries and little geopolitical gains from the objectives. A low cost, long duration mission requires a very stable civilization that expects to be interested in the mission returns for the last legs 1000s of years in the future.
The usual argument for delaying any mission is to assume faster/cheaper vehicles in the future. The high m strategy may work for the very nearest stars, but likely will be overtaken for the more distant stars.
Then there is the issue of what science can be achieved by a flyby mission. Will a flyby probe offer more useful information than a building a super-telescope at Sol? If one aim is to detect the state of any ET civilization, a telescope will provide more timely answers than any interstellar probe (Civilizations will rise and fall during the mission time of the m = small strategy).
The value of a probe is to provide information that may not be possible by any instrument located at Sol. Dropping off slow moving sub-probes that can explore the planets of the star system, even land on the worlds would be a huge gain. But the technology to slow down these daughter probes from the 0.1c of the mother ship has to be developed to make this a viable strategy.
My sense is that without a very great change in our human civilization with omnipresent national/corporate rivalries, we will not make the effort to send more than a handful or so of probes to the nearer stars, using the high m strategy to limit the mission times J2_i = distance_i x 10.
Alex, you mention some good points. First, in answer to your questions in the beginning: The time for the data transfer is not included – the star is considered to be explored, as soon as the probe reaches the star. I thought of this issue during the modeling and decided to exclude the time required for data transfer to avoid a “heigher weighting” of close stars. Of course, one could repeat the simulation with this issue included and see how the results change.
To your second question: Stars, that have already been visited by a probe, cannot be visited by a second probe. I assumed, that the additional gain in scientific return when visiting a star twice is lower compared to visiting two different stars.
I agree with most of your conclusions, which I really appreciate because they show that my article has been understood. Let me add two remarks:
I assume the probes to travel at an average velocity of 0.1 c. This means, that there is the possibility to slow down slightly before approaching a star system, if we assume that the cruise velocity is higher (say 0.15 c). Of course, one need to discuss the technological realization. When doing the literature review, I read about photogravitational assists which could be an option (covered earlier on this blog: https://centauri-dreams.org/2017/04/17/proxima-mission-fine-tuning-the-photogravitational-assist/).
Maybe this could help to increase the scientific return, as the probe would spend more time in the star system – to have a number here: through our solar system, the probe would rush within 3 days (assuming 0.1 c and taking twice the distance from neptun to Sol as reference). Honestly, I am not capable of judging whether this allows significantly higher investigation possibilities compared to placing a high-performance telescope near Sol. That’s why I am using Crawford’s paper as reference here ([6], cited above), who discusses the scientific return aspect for flyby mission in more detail. For instance, he mentions that flyby missions enable a much more detailed analysis of the atmospheric composition of a planet.
Hi, Johannes. Alex has a crucial point about the relative value of flyby probes and Solar-System-based telescopes. I would suggest that if you’re interested in optimal strategies, you need to be able to say how much science per dollar you think you’ll get from flyby probes, and how much from telescopes, in order to begin to optimise your spending. Remember also that the greatest scientific goal concerns the possibility of extraterrestrial life, and that after 45 years of surface exploration of Mars, it’s still not possible to say whether Mars has or does not have indigenous life! Therefore I suggest that the minimum requirement for an interstellar probe needs to be better landers and rovers than those deployed on Mars to date!
Best wishes, Stephen, Oxford, UK
Really interesting article Johannes. I wonder how this model would perform if the probes were intelligent, and could update their priorities as they learn more about new planetary systems.
As an example, if it turns out that white dwarves with hot Jupiters were more scientifically compelling than the original stellar score suggested, would intelligent probes be able to take this into account? Could they modify their routes with updated stellar scores, instead of having to rely on the information they were launched with from Earth?
I did not cover this in my model and simulation, but I think it’s a very nice idea to define a dynamic stellar metric.
In fact, I think it’s indispensable to provide the probes with some degree of intelligence, as they need to operate completely autonomously and, furthermore, we humans have no experience in exploring other star systems.
I would guess, that the exploration strategy would change in way, that the probes would try to explore as many stars as possible in the beginning to “learn” and update the stellar metric. Later, they probably will pick only the most promising targets, but this depends of course on the parametrization of the model.
However, if we assume a dynamic stellar score and allow the probes to modifiy their routes, we have to establish some communication link between the probes. Otherwise, one star might get visited by multiple probes. As further advantage of the inter-probe communication link, they could share their experiences to build a common knowledge, comparable to a swarm intelligence.
You should really check the Gaia EDR3 catalogue of nearby stars. It was cleared and checked in a very rigorous way and is the current standard of local neighbourhood systems. In principle It contains all known systems in a 100 pc radius (326 ly).
https://www.aanda.org/articles/aa/full_html/2021/05/aa39498-20/aa39498-20.html
I totally agree that the Gaia EDR3 would have been a better choice, but when it was published, I was already done with my model and generated the first results, so I did not want do more modifications on this.
This reminds me of logistics game theory, something that may be what is being used to maximize profits in the COVID supply chains problems. Two things that could decrease the period down to seven hundred years is the next 200 years of asteroid belt and solar system developments. Solar system wide laser or particle beam cannon arrays and chip probes that could use superconductive wave mechanics to allow speeds closer to light. The development of solar system wide optical interferometers would give details on what is in each system to better plan development.
Barnard’s Star is fast enough that a probe may not have to slow much if field effects allow gradual turning. Gliese 710 demands a fast fly-by.
I’ve often thought about the logistics of this problem, although I have approached it more from a route-selection perspective rather than a return-efficiency optimization model.
I conceive of a single mission, one capable of approximately <0.1 c final velocity which is achieved soon after launch. The goal is to select a route that visits several stars, all strung out in a more-or-less straight line (after correcting for proper motion). The probe would approach its first (nearest) destination and conduct a high-speed close flyby, transmitting its findings back to Earth. It would then alter course slightly (using gravity-assisted slingshot maneuvers or light sails to impart sufficient lateral delta-v to direct it to its next target. You will recall, our probe achieved most of its earth-relative radial velocity while still relatively near its launch point, whatever lateral velocity required to rendezvous with its next target would be much less, but it would accumulate over the long time it takes to get there.
By selecting several target destinations in an approximate straight line radially pointing away from Earth, several targets could be visited in sequence. Unfortunately, the spacing and location of the targets would dictate the selection, not their intrinsic properties or potential scientific value as a destination.
To fully quantify this model, one needs to know the final velocity of the probe (presumably achieved while relatively near Earth) and how much lateral delta-v the probe can generate after each encounter. I presume that a vehicle approaching another star at several percent of c will not be able to generate much of a gravitational slingshot velocity using purely dynamical interaction–it is approaching much faster than the escape velocity of the star. The energy gained by falling down the gravity well will be much less than the kinetic energy it acquired during its boost phase. Still, I'm not confident enough in my celestial mechanics to know if this is actually the case. Can a probe actually make right angle course changes by slingshotting around another star as is implied in the article? Perhaps a minor 1 or 2 degree course correction is the best we can hope for.
So what would a solar-neighborhood, long-term exploration program look like honoring these constraints? I visualize several Daedalus-type probes launched in all directions away from the sun. Each travels to a nearby stellar system, makes some observations and transmits its findings home, and then makes a minor course adjustment around that star to send it along to its next target, several parsecs farther out. The process is repeated at most, several times. By then, it is expected the home planet will have either lost interest, or developed a faster means of travel.
Interesting approach to do a route-based selection, thanks for sharing. Due to the selected objectives (mission duration and mission return), the routing efficiency is also considered by the algorithm in the approach I presented in the article – of course, without taking the flyby maneuver into account. By extending the model and implementing flyby dynamics, one could merge both approaches.
Regarding the deflection angle: You are certainly right, at the considered velocity regimes the maximum deflection angles only due to gravitational help is limited. I actually was thinking of setting a boundary of condition for my simulation, which limits the maximum possible deflection angle. However, in the end I did not implement it, for subsequent investigation this is certainly worth considering.
If you are more interested in this issue, maybe you want to have a look at two papers, if you don’t know them already:
Cartin: Exploration of the local solar neighborhood I: Fixed number of probes https://arxiv.org/abs/1304.0500
Moir & Barr: Analysis of interstellar spacecraft cycling between the sun and the near stars https://docplayer.net/100443535-Analysis-of-interstellar-spacecraft-cycling-between-the-sun-and-the-near-stars.html
They discuss the deflection angle limitations for interstellar flight, also under consideration of the heat load, which requires a trade off: For high velocity flybys, a very close encounter (small perihelion distance) is required to allow for significant deflection angles. However, slowing down may also cause problems, because the probe spends more time near the star, which increases the overall heat load. Also, the luminosity of the star has some impact.
A great synthesis of many ideas, thank you!
Multi-millennial plans and missions are way past the electoral cycles which shape agendas and policies by constraining perspectives: “Frankly my dear, I don’t give a damn …”. This even extends to the decision-making honchos in scientific, engineering and other bodies: “What’s in it for me/us?”.
Missions sent out with defined limits of exploration and electronic data return are akin to a blind man’s cane, albeit with greater sophistication in poking, prodding and sensing. A slime mold is what is needed to populate the galaxy: sufficient artificial general intelligence for survival and replication; and avenues to modify and expand it. That would imply the possibility to throw off the shackles of earthly politicking!
The ultimate problem with missions that only return data after centuries or millennia is that we really can’t guess what sort of data may be useful to people that far in the future. As other commenters have touched on, it’s very likely that any probe we send out with that long a travel time will a mere curiosity by the time it reaches its destination. Science and the rest of society will have moved on. Even today, functioning space probes are shut down because the data they return is no longer of interest or can be better obtained by other means.
The answer I think is to have the probes return data in the near to medium term, as well has when they reach their ultimate destinations. This will provide information that is immediately useful to us. If our descendants also find the data being returned useful, they’ll keep the probes operating. If not they’ll shut the probes down or stop monitoring them. The final choice will be theirs.
Thanks Johannes
A very interesting read and a lot to ponder.
Did you have a view of the nearby stars and how they would be explored with your model?
Thanks Edwin
Thanks Edwin. I am not sure if I understood your question correctly, so please let me know if you need further clarification.
The exploration procedure of each star system is not part of the model. For simplicity, I assume each star system to be explored as soon as the probe reaches the location of the star. Of course, for future work one could think of extending the model by allowing different exploration approaches (such as deorbiting, which would have a negative impact on the mission duration but a positive impact on the scientific return of the mission).
It seems in regard to star travel; I think needs one start by realizing our star is not a good star to travel from or to go to. And you don’t need planets unless they make a star system easier to enter and leave the solar system. So, start by finding best star, to travel to and to leave from which closest to Sol.
It seems possible that rather than a shining star, one looking for the nearest and best gravity well.
1) telescopic exploration, VR simulation: we aren’t even doing what is possible with current tech, a shame
2) learning to live anywhere in the universe: we will do that on the moon and Mars
3) growing the Solar Sytem economy: population x tech level
4) learning how to speed up, coast for decades, slow down: I favor nuclear; stasis pods; mass shot out the near front
Nuclear engines and “mass shooting out front” are both rockets or devices using Newton’s 3rd law of motion. There are insufficient for interstellar travel except at extremely low speeds.
Stasis pods are magic tech. They don’t exist, nor are they likely to.
The best way to suspend agents for interstellar flight is to use intelligent machines and just shut them off until the destination is reached. Even if you send frozen embryos or other forms of suspended animation in seed ships, you will need intelligent machines/robots to nurture humans from birth to adulthood.
While I admittedly only were read the first few paragraphs of the article, and was especially dismayed/surprised by the fact that there are compilations of data that are so poorly managed that they completely suggest that there are 50 stars closer to us than Alpha Centauri, I’m willing to say that multiple exploration like this don’t seem to be particularly fruitful.
Rather, I’m form or willing to put my eggs all in the one basket of faster than light travel which now seems to be at least within the realm of scientific possibility at this particular time. I again refer you to the Centauri article about Eric Lentz who was reported on a few months ago in about mid March of this year and had seemingly, found a solution to generating at least in principle a soliton space time configuration which would have super luminal properties. Now that it seems like at least it is practical in principle to achieve this goal that’s where I would put my money and effort. Better to wait a little longer for what appears to be a much better return than to follow these long wait times to do*exploration
You probably should have read more. The chart shows the various legs between stars on the journey. The first leg obviously cannot be less that the distance to the nearest star, but after that the legs depend on the separation between stars.
FTL travel would be wonderful, if it proved practical. But we really need to see some evidence beyond some math that suggests it may be possible in theory.
From the CD article I take this final quote from the Lentz paper:
“The energy required for this drive travelling at light speed encompassing a spacecraft of 100 meters in radius is on the order of hundreds of times of the mass of the planet Jupiter. The energy savings would need to be drastic, of approximately 30 orders of magnitude to be in range of modern nuclear fission reactors… Fortunately, several energy-saving mechanisms have been proposed in earlier research that can potentially lower the energy required by nearly 60 orders of magnitude.”
IDK if this is practical by any normal use of the term. I also wonder at the possible causality violation this technology, were it to exist, might cause, that is the oft-used objection to FTL flight and even FTL communication. Conversely, we know that STL travel is possible, albeit very difficult, and interstellar voyages are technically already underway with our outer planet probes, like Voyager. We already know in principle how to push probes to fractions of c by various means, so it is well within the realm of possibility that we could launch such probes within a century or so should we wish to.
This is why I hope Planet 9 is a grapefruit sized black hole. Have a very long cable in from of your massive craft to feed into the black hole…which pulls the craft forward at ever greater speed. Release and do a side burn to go slingshotting past.
The objections that you have raised are noted, but I would like to add further that the energy requirements seems only at this time to be transitory in terms of our understanding of what is needed to be generated. I feel fairly confident that in the future they are going to drastically be able to reduce the energy needs to something that’s in a far more manageable range. The main take away (and what was the truly) staggering aspect of his paper was he brought FTL travel out of the purview of being nonphysical to being at least possible; and that’s what truly matters.
Insofar as the causality violations that you mentioned, while I am not a relativist by technical training I have been able to at least absorb a good portion of the ideas from his initial paper on Special Relativity. I feel now fairly convinced that those people who apply those ideas to FTL situations have misunderstood the foundations on which SR is founded. The theory was not designed for that situation, yet people use it as if it applies universally. So that suggests to me that a new physics will exist in a situation where FTL applies. General relativity which seems to be the foundation of Lentz’s paper is a different beast altogether. To me current technology is simply not up to the task of doing what this gentleman suggest in a reasonable timeframe.
A sharp paradox recently came in my mind while I was thinking about black holes and the GW observations which could provide an answer to the question if FTL exists.
Any object falling into a black hole provides local protrusion of *apparent* event horizon after it plunges in; just like BH mergers result in deformed horizons which produce GW-detectable ringdown.
This ringdown reflects something that takes place deep inside BHs. The popular objection is that all information about falling bodies is already present before the plunge and the ringdown provides nothing new.
But imagine a massive spacecraft that descends into a SMBH with a Schrödinger’s cat onboard. When piloting AI records horizon passage, a robot opens up the box and observes the cat. If the cat is alive, the ship continues as before (the side effect would be the cat observing singularity). If it is dead, the robots triggers antimatter-powered pyrotechnic release and the ship separates into halves flying sideways relative to the prior trajectory as fast as possible.
Distant observer watches the BH with an ultra-powerful telescope and records whether the apparent horizon bulge flattens faster than expected.
Thus, he obtains an information which *hasn’t existed!* before the plunge, and travelled up the superluminal space waterfall from below the horizon.
I haven’t yet found anything about this paradox (or whether it is explained in some way), but to me it looks like something.
Perhaps a black hole is merely a collection of gravitons with all the matter and energy converted into gravitons via the huge fields that are present.
I tend to think that BH paradoxes imply that if there is anything below event horizon, than FTL exists and is physical. Conversely, if “c” is the true ultimate limit (and Alcubierre drive is unphysical after all), than there must be nothing inside event horizon, and all BH mass is concentrated near it.
There are some concepts describing it, like gravastar and similar ones. They all require different behavior of gravity near horizon, where infalling particles are accelerated to near-Planck energies relative to the structure that holds BH mass. But they are attractive in many ways. Paradoxes are resolved, and the firewall problem – too. Here the near-horizon structure IS the firewall, disintegrating all infalling matter, accelerated to near-speed-of-light, to the state of maximal entropy. My current favorite is https://arxiv.org/pdf/1311.4538.pdf. Utterly beautiful things happen there to the infalling matter.
At the same time, “nothing inside EH” does not imply that FTL is not physical. But if some of these models turns out to be real, we’ll likely have to prove FTL existence by some other way rather than observing GWs from mergers.
I still eagerly await the moment when LISA flies and returns her first data, turning noisy LIGO waveforms into something really hi-fi and bringing us the crispy clear picture of New Physics at last :-)
It doesn’t seem to be explicit, but does this analysis assume that all the probes are launched in a short time frame relative to the shortest trip, and then no more are launched?
It seems to me that a society capable of launching a number of 0.1C star probes capable of multi-thousand year lifetimes, and monitoring the data sent back over those thousands of years, would be a society capable of continuing to send probes. And improving at building them all the while! It certainly wouldn’t rely on the efforts of probes thousands of years obsolete, were it capable of launching more.
So, we should expect something more like probes being launched at intervals, and each probe being an improvement over the previous, in terms of speed and other capabilities.
We might even face a “Far Centaurus” problem, were we to launch to any other than the nearest stars, because propulsion improvements after probes were launched to distant destinations would result in later probes reaching them first, rendering the earlier probes mere historical curiosities, not useful efforts at information gathering!
Thus, it appears to me that the most straightforward approach is to launch single destination probes towards targets chosen in order of distance. This maximizes the early information return, and minimizes the chance of wasted probes. Only after some fundamental limit to propulsion performance had been hit would it make sense to do anything more complex.
Yes, the results presented above are based on the assumption that all probes are launched at the same time from Earth.
Nice idea, I agree with your thoughts. It would be interesting to see, how the results change, if we assume that the probes are launched subsequently (say 1 per 5 years) and each time the velocity is increased by 0.01c, to model some technological improvement. Also one could add a failure probability of each probe, which of course reduces with each probe being launched.
Is it possible to get the chart [9] with details for mission times within 100 years to show the returns (including the time to receive the return data for each star)? How do the curves with different m compare over that time period? [I presume that all strategies converge to about 47 years for the first return from Proxima. But thereafter?] Constraining the number of stars that can be searched has some impact too – worsening the mission duration for small m strategy?
Hey Alex, I had a closer look into that region: Due to the limited population size the algorithms provides only few solutions for very low mission durations. However, one finds that the curves for the high m strategies approximate the curves for the lower m. I guess, the reason for that behavior is that for very short mission timeframes there are not enough targets which are reachable in that time. For instance, it does not make sense to deploy 500 probes if there are only 50 star systems reachable within 200 years. Hence, the assumption of linear correlation between mission return and duration is not valid in that region.
I did not have the time to include the aspect of data transfer back to Earth, sorry. The problem is also, that during my thesis I had access to a more powerful computer while currently I am just using my private notebook with very low RAM, which makes it very uncomfortable to handle the large data.
Regarding your last point (constraining the star number): For my thesis, I did the same simulation using a smaller model with 1,000 stars. The results show, that the curves are slightly curved, even for the low m strategy. Hence, the impact of the model limitations sets in pretty early.
Thank you for this excellent piece of work, Johannes. If our species are to pass through the postulated “great filter”, we need bright young minds like yourself thinking and producing original work along these lines.
I would like to offer some thoughts which occurred to me while reading this blog post. Please bear with my verbal diarrhea.
Alas, sending probes at 0.1c to another star system is not achievable with current technology, and the way the world currently operates, may not happen in my lifetime or at all. It seems perpetually to be something we dream that the next generation might do. NASA is definitely not going to fund such a mission in the next few decades, if ever, and we are certainly not going to build and launch a Daedalus or Icarus style probe while sitting on our collective arses deep down in this gravity well we call Earth. Our best current technology can barely (I hope) and at great cost do a fly-by of an Oumaouma or Borisov type object. This sadly limits the usefulness of your hard work to the theoretical, maybe we can gain a better understanding of how interstellar civilizations will spread through the galaxy which may help a bit with the search for technological signatures.
Nay, if we are to pass this great filter, we need to look at smaller, but more achievable steps to get to a state where such an endeavor would be possible.
Operating from Earth, like we currently do, has the advantages of plenty of resources and energy sources readily available, and we certainly know how to manufacture things in 1g. But we have a very steep gravity well to climb out of, not to speak of our thick atmosphere, and the only way to do that currently is with very expensive chemical rockets.
We do have a Space Station in LEO where we are learning to do some stuff in microgravity, and to launch something big from LEO has the advantage of being some way out of the gravity well and above the thick atmosphere, so you could use electrical thrusters or solar sails from orbit. Sadly, we have no experience of building anything in LEO, and there are no resources there, so we must ferry all building materials up out of the gravity well and through the thick atmosphere with chemical rockets, again at prohibitive cost.
Gladly, it does seem that we have a fighting chance of establishing a hopefully permanent presence on the Moon within this decade. While the jury is still out on wether mr Musk’s Starship will achieve the great things he says it will, his Falcon rockets have certainly cut the cost of getting things into orbit rather substantially, and the Chinese seems to be trying to copy that, so maybe just our species can start inhabiting a second speck of dust in the foreseeable future, and hopefully once we have an established presence on Luna, we can start to learn-by-doing and mine the Moon for resources, and learn how to manufacture stuff using those resources.
Once we have learned how to use Luna’s resources to manufacture things, spreading to other dust specs will become more feasible. Luna’s gravity well is a lot less steep than Earth’s, and it is almost all the way out of Earth’s gravity well, and it has no atmosphere, so you could launch massive thing from there a lot easier, and you have more options. At first you could use chemical rockets, with methane and oxygen which you don’t have to ferry there from Earth, but you could also develop other technologies. Rail guns, space elevators, even Orion style nuclear launch vehicles, among many others, comes to mind. Energy sources on Luna is also plentiful. At first, solar power is a good option, but later on nuclear power plants, using fuel which were mined there can be developed.
So, Luna seems achievable in a reasonable time frame. Advantages include plenty of resources and energy sources, shallow gravity well, almost all the way out of Earth’s gravity well, no atmospheric drag. It is still close enough to home that it may make some business sense for an entrepreneur to establish mining and manufacturing capabilities there in co-operation with government agencies. Maybe by the time this happens, mr Musk will have established a base on Mars, maybe not, but that base will be largely on its own because you can only go there from Earth once every 26 months, whereas if he did start building a base on Mars, that would mean that Starship did work, and you could conceivably launch Starships and entrepreneurs to the Moon daily if you wished, and at a much lower cost.
In any case, once the capability to manufacture and fuel space ships on Luna has been established, the energy cost to send a probe to not only fly by but rendezvous with an interstellar comet or Oumaouma type object drops dramatically. Also the cost of building an Icarus type interstellar probe in Lunar orbit becomes somewhat less daunting compared to Earth, because ferrying building materials up into Lunar orbit is a lot easier than from Earth.
Now it may conceivably occur to some entrepreneurial minded person to establish mining operations on a Near Earth Asteroid. It could be mined for resources, eventually hollowed out, and you could spin it up and build an O’Neill type habitat. Also, energy sources are plentiful and it would seem there are quite a number of these dust specs we could spread our species’ presence to. If you wanted to establish manufacturing capabilities on such an asteroid and, let’s say build a probe to intercept an interstellar comet, it could be launched from an asteroid with much less energy cost that from the Moon, because you don’t have the Moon’s gravity well to climb out of, and you’re all the way out of the Earth’s gravity well. NASA could at that time, conceivably award an entrepreneur a contract to build such a probe.
If you wanted to build an Icarus style probe at an asteroid, it could also be done at much less energy cost than at the Moon, because you don’t have to ferry building materials out of any kind of gravity well to construct the craft with. This could put building such a craft within the realms of possibility. It would still come at a prohibitive cost, though, and I don’t see it making any kind of business sense for an entrepreneur to attempt something like that. It would still have to be done by co-operation of our species as a whole. But it could be done.
Much more likely, though, if one entrepreneur starts earning a living from operating mining and manufacturing operations on an asteroid, others will likely follow. Contracts could be awarded for building probes to the outer planets, KBO’s etc. It may even make business sense for such entrepreneurs to send their own exploration missions to other asteroids in order to expand their mining and manufacturing operations.
And here is where I think your work could be adapted to the exploration of asteroids. You would have to contend with moving targets, though, among many other adaptations, but you could build a model of the spread of our species into the asteroid belt and beyond, and this could be of tremendous use for aspiring space entrepreneurs to optimize the expansion of their operations and gain the edge over competitors.
Once we have established manufacturing capabilities on asteroids, a plethora of options becomes available. For instance, you could build a truly huge telescope on an asteroid, far away from any gravitational stresses. If built on an asteroid that orbits at a high angle out of the ecliptic, there is a lot less interplanetary dust to peer through, and it becomes easier to spot and study very faint objects. You could identify objects to send probes to in the far outer reaches of the solar system, for instance.
You could even accelerate such a telescope ever so gently with ion propulsion to reach the Sun’s gravitational focal point in a reasonable time frame, and so start to REALLY explore nearby stars and their planets. Once manufacturing costs drops, entrepreneurs may start getting awarded contracts to do just that.
It may make business sense to start spreading to asteroids further from the Sun. It is easier to launch probes from there, as you are further out of the Sun’s gravity well already, but solar power becomes less of an option to power your operations with the farther from the Sun you get. So you will have to develop technologies and gain experience living and manufacturing further and further from the Sun. An entrepreneur might manufacture a large solar powered laser on an asteroid near the Sun to power operations on asteroid in the main belt, or even a Centaur, and so gain experience with that. Maybe this will be how we will slowly start to build our Dyson swarm, as more and more energy is needed.
One day, we will maybe be able to not only rendezvous and study an interstellar object passing through our system, but land on it and establish manufacturing operations there. You could build, among other things, a telescope to look for objects in or close to the interstellar object’s future trajectory, and build probes to study such newly found objects, as the cost to launch such a probe from Earth is very high, but if you’re already out there it is a lot more achievable. You could also build another space ship to intercept and land on such a newly found object of interest, and spread your mining and manufacturing operations there. And so we may slow-boat our way to other star systems.
Yeah, you say, but what if newer technology gets developed and overtakes your slow boat? Well I’m sure that a business which made a business case for operating on an interstellar comet, will certainly have high quality communication with Earth, and any new technologies that are developed close to Earth will be available to be implemented on your manufacturing plant which is on the way out of the Solar sustem already. You could find a way to manufacture a space ship with the new technology at yor plant which is already headed out at a considerable speed, and launch it from there.
If we just dream about ships exploring star systems at 0.1c, they will never be built, and we will never become interstellar. If we take baby steps though, at each step learning by doing and gaining experience before making the next small step, we may just pass the great filter and become a multi-stellar species.
And once we have spread operations to, not just flew by, our first star system, we may find that it becomes a lot easier to jump from there to multiple other star systems. As was mentioned elsewhere in the comments, our Sun is not a great place to expand to other close-by stars from.
Thanks a lot for your comment, I found it very interesting to read through your roadmap for becoming a multi-stellar species.
Of course, I am well aware that the exploration missions as I described them above are very ambitious (to say it conservatively), from the current perspective they appear unfeasible. Accordingly, the usefulness of the results may be limited, as you already stated.
What I think is more valuable, as I tried to explain in the introduction, is the methodology (problem class definition + star model + genetic algorithm). I would compare it to a toolbox, which can be used to solve similiar problems or the same problem with different assumptions. For instance, if future shows that we are able to travel at much higher speeds (as I read somewhere in the comments), the same methods can be used. Also, as you mentioned, one could use the methods to analyse strategies for asteroid exploration/exploitation.
Yes, that is the true value of your work, the methodology, which I think will be incredibly useful if adapted to different closer to home scenarios.
Of course there may be many flaws in my pet roadmap, as I’m sure others will readily point out, but as we do and learn I am sure your toolbox will be adapted and developed further as the road ahead becomes clearer.
Please continue to work in this field if possible, your work is a breath of fresh air and I hope to see lots more where that came from.
This was an engaging and thoughtful essay close to heart of Centauri dreams. So many developments these days are about target exoplanets.
Consequently, we become accustomed to reading more about observations than how to get there. Having good targets is a welcome development, nonetheless.
In reading this exercise it evokes memories both from the s/f literature and other applications of optimization or operations research.
A moment quite akin to this launch scenario in the lit was Robert Heinlein’s “Time for the Stars”, the story of multi-launches of relativistic velocity spacecraft linked in communication to Earth by telepathic twins, covering several issues or considerations in a 1950s context. When I had the fever and flu in grade school, I could see
this some of this in my sleep… “Bread cast on waters…” was the foundation’s motto that launched this effort. And they were confronted with something of the same issues, even if a lot of the story seemed like
serving on a naval ship in distant waters.
The other end, optimization or operations research, that is more difficult to comment on. With each decade more number crunching and iterative fire power is provided. There are indeed elements of both minimizing energy expenditure ( flight path), but also trying to obtain a maximum benefit ( such as war games). And in the latter case, it seems difficult to tie down what the benefit will be other than the maximum
exploration and data returned obtained for a budget of ships launched in the name of a metaphorical Hellena.
I might be missing some of the analysis, but sometimes we the audience
benefit from the examples. So here goes:
And let’s say that the immediate explorations ( attached to Gaia) are with 100 parsecs. Velocities limited 0.1 c in cruise. So we have a campaign on order of 3500 years outward and up to 350 years added
for report back.
For example, when does a somewhat decelerated probe reveal more to the home planet than a large telescope vs. the lag?
Or is the probe already following up on telescopic leads?
If exploration is devoted to exoplanets in habitable zones, how do you weigh one prospective system among perhaps a million candidate stars vs. another?
It seems like the far edges of this exploratory sphere the numbers increased with radius cubed and the unknowns likely increase with the reduced telescopic resolution or signals identified. Less precise measures will reduce the selectivity of the search and the ability to respond with corrections.
Correspondingly, you could keep going or brake to remain an observer in a prized target. Authenticating the value of the target will likely be achieved with increased information at the terrestrial nerve center.
Reckoning from when the Pioneers and Voyagers were launched, I should think that we can increase our capabilities of launching probes many magnitudes. If nothing else, by devising orbital facilities for accelerating interstellar probe devices. Maybe even exploiting their
recoil to launch world ships in the opposite direction. Well, mini worlds…
Best regards and thanks!
Thanks for sharing your thoughts! In the end, I think we need to push the limits at each research frontier: Trying to learn more about star systems characteristics and possible targets (ideally identify more star systems that host habitable planets, or at least estimating the probability), but also discussing how to get there. Both goes hand in hand – it would be sad if we identify more and more exoplanets, as we do currently in large number, but stop thinking about ways how to go there.
The question, how to quantify the scientific value of an exploration mission is very complex and also highly subjective: biologists will have a different focus compared to astrophycicists. So beside the common, overarching goal to find a habitable planet or even extraterrestrial life, there are a lot of different subgoals which can be weighted differently. In my thesis, I suggested a stellar metric, which tries to consider the scientific factor (stellar characteristics such as metallicity), data quality (how reliable are the information we have), and the mission suitability (any advantages for the mission beside the scientific factor, e. g. resources for exploitation or accessibilty). Of course, it is up to oneself, how to weight those factors to calculate the final stellar score of the star.
However, even if we can agree on a common goal, there is still the problem that at the moment we have a very limited knowledge of star systems. E. g. from what I found in literature, I see that the impact of the spectral class of a star on the planet habitability is still discussed. The more we know about star systems, the better we can decide, if they are worth visiting or not. Even for very distant targets, which are difficult to observe in precision, as you mentioned, we could at least do some statistical estimates based on our experiences – experiences, that we don’t have yet.
That is why, from the current perspective, we would learn a lot also by placing a high-power telescope near Sol. But I am sure that there will be a point (whenever it will be), from where we need to send out a probe to find out more.
Time will continually change our technological capability so we need to focus on what we know now, not what might be possible in the future, so FTL goes out the window from my point of view. We think from the StarShot work that the best approach is small lig weight probes which can be accelerated to the greatest velocities. Would it not be best to focus on the closest stars with planets in their habitable zones? This would limit the time taken and the cost. Your work is much appreciated and very valuable Johannes and thank you for sharing it with us. However it isn’t likely that we will explore out to about 330 light years at any time in the near future. I suggest we focus on stars with 20 or 30 light years with promise of planets in the habitable zone. I haven’t investigated how many star systems that would be but it might be manageable to send probes to them in the next 100 years or so. That might be a feasible goal if we make it as a species through the next 50 years or so while retaining or increasing our technical capabilities. Good luck with your future research :)!
I agree, limiting the maximum distance of the considered stars would enable missions with less ambitious timeframes. Just to give you a number here: My Gaia based model says, that there are about 200 stars within a distance of 30 ly (the number increases with r^3). Of course we don’t know for all of them if they are hosting a planet in the habitable zone, but at least some of them are known (or at least presumed) to do so. So, probably enough promising targets for sending a probe.
However, what I’ve learned thanks to many of the commenters, we could already gain valuable knowledge from a high-power telescope, which is especially the case for those near-by targets. Hence, for launching an interstellar probe maybe it’s better to consider also more distant targets, that are more difficult to observe.
Ruminating further or overnight about this question: At whatever magnitude this task is undertaken in the future, J. Lebert’s issue or dilemma remains lurking in the background. For a long time, this issue seldom got past the idea that a device or ship would set out toward a target and be destined to be bypassed by a later improved model. Sure, that’s possible. But now that we are also rich in targets and have space borne observing systems improving faster than spacecraft, it was about time this exploration or transit problem was revisited.
Like many issues confronting society it might not be overtly solved by optimization (e.g., consider the deliberations for government contracts for infrastructure or even spacecraft), but analytical tools are usually very welcome to such councils that decide these matters.
However, some simple illustrations of the difficulty establishing benefits might be in order. For example, the planner could be confronted with choices like heading for a system with two terrestrial worlds on the edges of a presumed HZ… or one directly in the center.
Even if an algorithm had a simple discrimination rule for the case, adherents or participants in the process will likely argue for each because one or the other system causes their more narrowly focused scientific communities more excitement. Next, we could examine just having real estate accessible to landing ( verifiably 0.3 to 2.0 g surface gravity) or a genuine biosignature associated O2, etc.
When you get down to these levels of knowledge, you know where you want to go already. Then it becomes how many other visits do you have to pile up before your score with less emergent biological candidates add up to the value of a clear signal.
No problem? You might want to hang around in the biologically active system, canceling out other surveys.
Of course, the rules could be altered. And that’s a significant point. It’s not that this is an exercise in futility, but in its infancy, as it were, and this is a pioneering exercise. While we have a lot of information on
algorithm operations here already. In cases such as linear programming for allocating resources to run up scores, the objectives of a particular problem and the constraints set on it can vary. The constraints and objectives (penalty or benefit functions) can be concocted in light of having such a tool, but have to take into consideration issues such as described above: Criteria for target selection, stay times, the role of solar system based assets such as
large telescopes (e.g., you don’t want a probe to tell the same thing you found out ten years out about a system – but only 500 years later).
I don’t expect the author to come back with all that next week, but I look forward to all of us having an enjoyable opportunity to consider such issues more analytically. At least in this instance we won’t be rushed.
One other comment. Bryson et. al. from 2020 have suggested there are possibly 4 Earth-like planets within 30 light years of Earth. They based their calculations on Kepler data I believe. If we could determine actual locations for Earth-like planets within this distance, from TESS and other observation platforms this could give us our first real set of high value targets. It would be an additional input for your work and similar efforts Johannes.
Thanks for that hint, Gary. Of course, the more we know about a star system, the easier we can determine its stellar score. A star, that is known to host an earth-like planet has certainly a high value for our mission.
However, something which came to my mind already during writing the thesis, is that we have to be aware of our biased assumptions, as we only know our planet that has generated intelligent life: Is an earth-like planet orbiting around a sun-like star really the best target we can aim for? Or are there maybe other constellations which are actually a better choice when searching for habitable planets?
So, narrowing our search by focusing on earth-like planets may exclude other promising targets directly from the beginning.
I can’t get into this idea. I’m not that confident Earth will be habitable in a century, let alone planning space missions; but if it is who knows what they might be able to accomplish? Besides, the ideas here seem like a simple simulation not relevant to potential goals.
Flying past all the stars in a travelling-salesman fashion over thousands of years implies a lack of confidence in any further improvements in astronomy. But I’ve gone from not knowing as a child if we would *ever* discover another planet, to seeing a paper here about which way the winds blow on a tidally locked world around another star! How can any six thousand year mission pay off, even if the probe is shielded with adamantium?
Surveying all the nearby stars implies a lack of desire to boldly go beyond. A straight line seems more likely to reach the border of the Galactic Federation (or the Saberhagen Surprise).
Above all, stars are not dots. Some may have terraformable planets. Some may be suspected to have ecosystems of their own. Some are oddities – pulsars, black holes, something that can draw the eye of everyone who turns a sense organ toward the sky, and to which any of them might send probes of their own. Or they might notice if humans can unfurl 100 square kilometers of solar sail and block the pulses in a sensible pattern.
We might want many different missions to different kinds of places – some missions brutally industrial in nature, some scrupulously diplomatic and scientific, some paranoid and furtive, or perhaps excessively confident and welcoming contact.
No doubt everything would be planned, but very rarely should any two launches be part of the *same* plan. Every person, organization or culture taking on an exploration mission would need and want to set their own course, on Earth and beyond it.
Perhaps the best time to launch a fleet of interstellar probes is just BEFORE the anticipated collapse of our technical civilization. We can always hope that enough technology survives, or can be reconstituted, so that by the time the probes arrive we can pick up their reports.
IMO, the main point that this research makes is to show that optimization in principle applies to interstellar planning and it is possible to tailor strategies according to outcome. When the whole effort is measured in quadrillions of future dollars, it really means much. Of course, real detailed optimizations would be vastly more complex that the model that demonstrates how reasonable it is.
I thought of a similar and much more near-term task. As many have commented, even truly massive Solar-system-based observation projects would cost drastically less than a fleet of interstellar probes, and require much less advanced technology. Besides, the results are returned almost immediately compared to STL interstellar probes.
An optimization of an array of Solar gravitational lens observatories is what comes in mind. To observe extrasolar planetary system, a modest-to-big-sized telescope with a coronograph is sent to a point opposite to target system, at the 700 – 1000 AU distance from the Sun. Through SGL, even distant exoplanets could be observed in much detail and a precise “exploration value” could be assigned to each system.
The ultimate centuries-long-term task is to make an exhaustive survey of say, 1000 parsec-sphere, characterizing exoplanets based on their:
(1) colonizability
(2) habitability (which is not the same as (1)),
(3) in-situ exploration value, i.e., for some rare or peculiar life forms or ruins of long-dead civilizations: xenobiology and SETA surveys, both likely producing targets within long-term reach of advanced STL interstellar probes
(4) signs of currently active ETI (likely much farther away than targets of (3))
The task structure is quite different than for interstellar strategy. The more observatories, the more coverage. There is a tradeoff between lateral repositioning (requiring time and delta-vee) to observe several close targets, and more detailed study of a single close target accompanied with more background observations (a single close system with _all_ targets within several arcminutes of it vs. several close systems and _some_ background targets). Some observatories would “stick” to targets if they prove interesting, for some time based on how much interesting the target turned out to be.
A big unknown is whether extraterrestrial tech is already present at solar focal sphere, in example – gravitational lens communication relays.
There are already two approaches to sending observatories to SGL – cheaper and faster Plasma Magnet sail-based ones described some posts earlier here on Centauri Dreams (albeit less TRL and almost certainly very limited delta-vee for lateral repositioning), and nuclear-reactor electric propulsion: slower but more robust and with tons of delta-vee, so that maintaining position against orbital motion could almost be neglected and much repositioning is available.
This really could provide a 2.0. input for future optimizations of interstellar in-situ exploration!
Repositioning the probes on the SGL to travel from star to star focal lines is definitely easier and faster than actual travel from star to star. Even the shortest leg is 1 ly, i.e. 10 years of travel, yet the arc on the 550 AU spherical surface could be traversed with relatively slow velocity and needed delta_V. It offers all the advantages of a telescope and the probes, unless the probes can do very closeup imaging and even sample collection and analysis using daughter probes. Even chemical rockets could reach the SGL in about the same time as a 0.1c probe could reach Proxima, and more powerful propulsion techniques could reach it even more quickly and generate results in a fraction of the time an interstellar flyby probe could do, at a fraction of the energy and $ costs.
It would be very interesting to do the same optimization experiment, but using angular separation as the “distance” measure, with a value factor that is inversely proportional to a function of the actual stellar distance in ly (as distance reduces target resolution). As Astronist has noted, even landers have so far failed to find life on Mars. A lander or atmospheric flyer would be most useful on a planet where surface life is very evident (such as depicted in Wayne Douglas Barlowe’s Expedition: Being an account in words and artwork of the 2358 AD voyage to Darwin IV(. To me, that is where an interstellar probe/ship would have an insuperable scientific advantage that a telescope could never match. But one needs to be patient unless effective FTL interstellar travel is possible. [I am currently reading Stanislaw Lem’s “Fiasco”, where this is achieved by using cryosleep and subsequent time reversal in a black hole, a very novel, if fictitious, way to solve the problem without needing superluminal flight.]
While I would opt to take any advantage of gravitational lensing at 550 AU and further on, I am still puzzled about what or how would one control the field of view.
For example, if we were to set up to survey a particular star system, I suspect that the line of sight initially would be to the star. Thereafter, one could expect a search for a planet of interest – if this information was not already available in a catalog.
But given that, I would like to see further background on changes in aperture, resolution or magnification. After all, you don’t have a telescope mount that you can swivel; angular shifts would need to be obtained with thrust maneuvers. Assuming these things can be
mechanized, some AI might do some of the above.
But considering the light lag at 550 AU – 3.183 days…. There are HZ planets around red dwarfs with periods on that order.
And if an object is a parsec away, then an AU is an arcsec of separation. If this is something akin to a lever, at 550 AUs, the corresponding distance to stay on focus would be 272,700 kilometers or 1/550th of an AU. And that’s just one target. Unless a FOV of a few arc secs can be sustained.
The sticking point is still the powerful laser system:
https://amp-interestingengineering-com.cdn.ampproject.org/c/s/amp.interestingengineering.com/laser-powered-lightsail-could-reach-alpha-centauri-in-20-years
The communications issue is huge as well. No mission without solving it.
This is an interesting subject, which was first explored by the late James Strong, a Council member of the British Interplanetary Society, in Spaceflight magazine in 1970.
Strong sought to work out which were the most rewarding stars to visit from the Earth. He did not consider the timescale or speed aspects, as they didn’t really really affect the results. The assumption was a star-hopping strategy, that probes sent out would (eventually) be crewed ones, and that colonies would be founded on neighbouring systems from which in due course further probes would be sent. That is not too unlike the “mother-ship” strategy of the present article. There is a shared implication that interstellar travel will, for a long time at least, be difficult and expensive to resource.
Strong came to his conclusions by looking at star maps. I took his work further by using a computer together with distance penalties and objectively generated scores for the “attractiveness” of different stars.
Using the same algorithm, I also examined the likelihood that our solar system might be encountered by star-faring aliens on their way out from the centre of the Galaxy. The answer seemed to be: not very good, unless the aliens determine to go via Alpha Centauri, which system has a high attractiveness value.
“The Direction of Interstellar Exploration”, by A. Orme, pp 397-401, Spaceflight, Vol 21, No 10 (Oct 1979)
Didn’t see that you incorporated the paper showing a trip to Sirius would take less time than one to Proxima, because of accel-decel times for an orbital science mission.
was posted to Arxiv couple years ago.