We’ve talked about the ongoing work at the Jet Propulsion Society on the Sun’s gravitational focus at some length, most recently in JPL Work on a Gravitational Lensing Mission, where I looked at Slava Turyshev and team’s Phase II report to the NASA Innovative Advanced Concepts office. The team is now deep into the work on their Phase III NIAC study, with a new paper available in preprint form. Dr. Turyshev tells me it can be considered a summary as well as an extension of previous results, and today I want to look at the significance of one aspect of this extension.
There are numerous reasons for getting a spacecraft to the distance needed to exploit the Sun’s gravitational lens – where the mass of our star bends the light of objects behind it to produce a lens with extraordinary properties. The paper, titled “Resolved Imaging of Exoplanets with the Solar Gravitational Lens,” notes that at optical or near-optical wavelengths, the amplification of light is on the order of ~ 2 X 1011, with equally impressive angular resolution. If we can reach this region beginning at 550 AU from the Sun, we can perform direct imaging of exoplanets.
We’re talking multi-pixel images, and not just of huge gas giants. Images of planets the size of Earth around nearby stars, in the habitable zone and potentially life-bearing.
Other methods of observation give way to the power of the solar gravitational lens (SGL) when we consider that, according to Turyshev and co-author Viktor Toth’s calculations, to get a multi-pixel image of an Earth-class planet at 30 parsecs with a diffraction-limited telescope, we would need an aperture of 90 kilometers, hardly a practical proposition. Optical interferometers, too, are problematic, for even they require long-baselines and apertures in the tens of meters, each equipped with its own coronagraph (or conceivably a starshade) to block stellar light. As the paper notes:
Even with these parameters, interferometers would require integration times of hundreds of thousands to millions of years to reach a reasonable signal-to-noise ratio (SNR) of ? 7 to overcome the noise from exo-zodiacal light. As a result, direct resolved imaging of terrestrial exoplanets relying on conventional astronomical techniques and instruments is not feasible.
Integration time is essentially the time it takes to gather all the data that will result in the final image. Obviously, we’re not going to send a mission to the gravitational lensing region if it takes a million years to gather up the needed data.
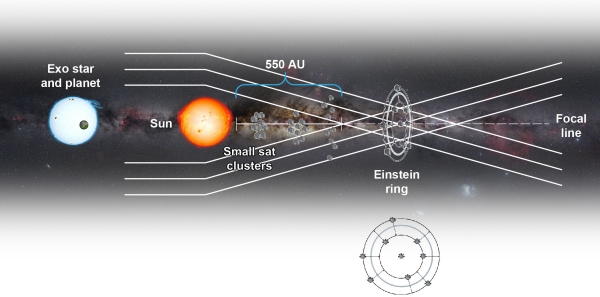
Image: Various approaches will emerge about the kind of spacecraft that might fly a mission to the gravitational focus of the Sun. In this image (not taken from the Turyshev et al. paper), swarms of small solar sail-powered spacecraft are depicted that could fly to a spot where our Sun’s gravity distorts and magnifies the light from a nearby star system, allowing us to capture a sharp image of an Earth-like exoplanet. Credit: NASA/The Aerospace Corporation.
But once we reach the needed distance, how do we collect an image? Turyshev’s team has been studying the imaging capabilities of the gravitational lens and analyzing its optical properties, allowing the scientists to model the deconvolution of an image acquired by a spacecraft at these distances from the Sun. Deconvolution means reducing noise and hence sharpening the image with enhanced contrast, as we do when removing atmospheric effects from images taken from the ground.
All of this becomes problematic when we’re using the Sun’s gravitational lens, for we are observing exoplanet light in the form of an ‘Einstein ring’ around the Sun, where lensed light from the background object appears in the form of a circle. This runs into complications from the Sun’s corona, which produces significant noise in the signal. The paper examines the team’s work on solar coronagraphs to block coronal light while letting through light from the Einstein ring. An annular coronagraph aboard the spacecraft seems a workable solution. For more on this, see the paper.
An earlier study analyzed the solar corona’s role in reducing the signal-to-noise ratio, which extended the time needed to integrate the full image. In that work, the time needed to recover a complex multi-pixel image from a nearby exoplanet was well beyond the scope of a practical mission. But the new paper presents an updated model for the solar corona modeling whose results have been validated in numerical simulations under various methods of deconvolution. What leaps out here is the issue of pixel spacing in the image plane. The results demonstrate that a mission for high resolution exoplanet imaging is, in the authors’ words, ‘manifestly feasible.’
Pixel spacing is an issue because of the size of the image we are trying to recover. The image of an exoplanet the size of the Earth at 1.3 parsecs, which is essentially the distance of Proxima Centauri from the Earth, when projected onto an image plane at 1200 AU from the Sun, is almost 60 kilometers wide. We are trying to create a megapixel image, and must take account of the fact that individual image pixels are not adjacent. In this case, they are 60 meters apart. It turns out that this actually reduces the integration time of the data to produce the image we are looking for.
From the paper [italics mine]:
We estimated the impact of mission parameters on the resulting integration time. We found that, as expected, the integration time is proportional to the square of the total number of pixels that are being imaged. We also found, however, that the integration time is reduced when pixels are not adjacent, at a rate proportional to the inverse square of the pixel spacing.
Consequently, using a fictitious Earth-like planet at the Proxima Centauri system at z0 = 1.3 pc from the Earth, we found that a total cumulative integration time of less than 2 months is sufficient to obtain a high quality, megapixel scale deconvolved image of that planet. Furthermore, even for a planet at 30 pc from the Earth, good quality deconvolution at intermediate resolutions is possible using integration times that are comfortably consistent with a realistic space mission.

Image: This is Figure 5 from the paper. In the caption, PSF refers to the Point Spread Function, which is essentially the response of the light-gathering instrument to the object studied. It measures how much the light has been distorted by the instrument. Here the SGL itself is considered as the source of the distortion. The full caption: Simulated monochromatic imaging of an exo-Earth at z0 = 1.3 pc from z = 1200 AU at N = 1024 × 1024 pixel resolution using the SGL. Left: the original image. Middle: the image convolved with the SGL PSF, with noise added at SNRC = 187, consistent with a total integration time of ?47 days. Right: the result of deconvolution, yielding an image with SNRR = 11.4. Credit: Turyshev et al.
The solar gravity lens presents itself not as a single focal point but a cylinder, meaning that we can stay within the focus as we move further from the Sun. The authors find that as the spacecraft moves ever further out, the signal to noise ratio improves. This heightening in resolution persists even with the shorter integration times, allowing us to study effects like planetary rotation. This is, of course, ongoing work, but these results cannot but be seen as encouraging for the concept of a mission to the gravity focus, giving us priceless information for future interstellar probes.
The paper is Turyshev & Toth., “Resolved imaging of exoplanets with the solar gravitational lens,” available for now only as a preprint. The Phase II NIAC report is Turyshev et al., “Direct Multipixel Imaging and Spectroscopy of an Exoplanet with a Solar Gravity Lens Mission,” Final Report NASA Innovative Advanced Concepts Phase II (2020). Full text.



So, we’ve got this hypothetical planet, whose image is 60 km wide. If it were standing still, that would be grand.
But, plugging Earth’s numbers in, the planet’s image would actually be moving around in an ellipse with a major axis of about 1.4 million km.
If the image were moving in a straight line, that wouldn’t be a big deal. (Actually, it will be, in addition to other motions, but compensating is almost trivial.) But unless you’ve got basically unlimited delta-v for station keeping, you’re only going to be in a position to do imaging for a limited period each “year”, when it comes back around. OTHO, each time it came back around you could scan another line across it.
Also, the planet will be rotating while being imaged.
None of this means that the imaging task is impossible, but the paper does NOT take them into account: “We also have not yet accounted
for the aforementioned temporal effects, including planetary motion, rotation, and varying illumination.”
They imply a longer period to collect a decent image, and because the integration time is limited unless you have massive delta-V, a larger telescope on the probe. The analysis was strictly best case and unrealistic, essentially imaging an exo-spherical cow.
Let’s say earth is 12k km wide, image is 60km wide, 12k/60=200.
Earth orbital speed is 30km/s, max image speed is 30/200=150m/s.
The delta-V required to follow planet image doesn’t seem to be impossible, and acceleration needed would be minuscule and well within capability of ion drive.
As for rotation, obvious we need to figure out the rotation period first, after that, it is just a matter of accumulating data over time and refine the image.
My gut feeling is, the biggest challenging is to send the probe to 550+ AU with enough mass and short enough time, if we can do that, all the others are comparably easier.
The first mission goes the other side of the
Sun from the galactic core-second? From Andromeda…third, Gliese 710…these don’t move much. Save Barnard’s Star for last after a lot of practice.
Here’s a thought – what about a static Newtonian reflector along the image tract, bouncing the light towards the main telescope detector?
Alternate could be a Fresnel type lens focusing the light to a main telescope detector.
Hi Paul
Fascinating work. Flipping it to the SETI quest, it seems a perfect technology for ETI’s to monitor their neighbouring star systems. Could the same gravitational amplification be their preferred means for transmitting data back from other systems? Seems logical too and at least one preprint has suggested looking at the line-of-sight on the other side of the Sun from possible target stars for any leakage from such signalling.
Stephen Baxter used it to great effect in his “Manifold: Space” (1999) novel, having the bio-mechanical Gaijin teleport between the stars by using their gravitational lenses. Greg Benford used it to spy on other star systems in “Across the Sea of Suns” (1983), though with a bit of artistic license he had one such lens looking at multiple star systems.
Turyshev & Toth continue to produce beautiful and highly useful work. I (like you, Paul) have been tracking the “gravscope” since Claudio Maccone’s first analyses of the mission issues, and the news just keeps improving with every fresh paper. Of all proposed space missions, this one is my personal favourite.
Doesn’t this invalidate the fear-mongering arguments about METI?
Only if ETI can determine the state of human technology from their imaging of Earth and that their sensors are in alignment with our Earth’s orbit around the sun.
METI signals leave no doubt as to the presence of technological species, and the signals can be sent to any star in the firmament.
The alignment issue is not so critical if ETI has local observation of the Earth and an SGL-based transmitter[s] to the ETI homeworld. [I think we had a post about such interstellar communication networks.]
“Better to remain radio silent and be thought a technological race than to METI and remove all doubt?” ;)
Needed a good laugh! Thanks.
Something that may make a difference in the amount of light coming from the solar corona is when the sun is at sunspot minimum. Coronal mass ejection (CME) at at their lowest in that time period. The spacecraft position should also be placed so that it is looking thru the corona at the star and exoplanets from the sun’s north or south pole since this has a much smaller amount of light coming polar corona.
http://paulnoll.com/China/Eclipse/I-eclipse-pic-big.jpg
Some comments;
1. Contrary to the previous post, the solar sail using a sundiver maneuver to reach 25AU/yr is deemed feasible within the same time frame as the SLS Block 1B approach, with far low cost. The perihelion distance is as little as 0.1 AU. For context, the Parker Solar Probe perihelion is 0.046 AU. Why the difference of opinion?
2. I am not clear about what the telescope does at the SGL. Each deconvolution is to create a 1 pixel representation of the target, requiring 1 million such pixels. If the image is spread out across 60 km, does this mean the telescope has to follow a complex path (because the planet and star is moving as well) to act as a raster tracker for the image? The text suggests that the telescope just has to slew to collect the data for the many pixels to be deconvolved. To me, that just suggests changing the pointing direction. Can someone explain what is happening exactly?
3. That “reasonable” sized telescope with 1-2m lenses can achieve 1 megapixel images within months is extremely impressive. While I won’t live long enough to see the result, I would be very in favor of such a mission if it proved technologically viable.
4. The NIAC report indicates that the telescope would use onboard AI for a number of purposes. Mention is made of Numenta’s HTM model for neural networks. I wonder if the use of AI can be used to best navigate the telescope when imaging the target as prior work has shown that such ANN techniques can surpass numerical modeling in speed for deriving solutions.
5. Lastly, the “string of pearls” approach for communication and redundancy would be very useful for increasing the number of telescopes to reduce the integration time for imaging. As suggested, they would allow for imaging multiple exoplanets that are in the same general field of view. This “swarm” approach solves the one target only issue of SGL missions when competing with other telescope projects. It is also an obvious extension of the idea of using many cheap, fast probes doing flybys to constantly monitor targets in our system, handing off the task to a stream of probes with short observing time at each target, but offering fast data collection rather than waiting years for a slow intercept and possible orbital craft to make such observations. This is particularly useful for rapidly evolving and transient phenomena.
I’ve only briefly skimmed the first paper and there appears to be an important omission. The planet is not sitting still waiting for its picture to be taken. It has both a proper motion and it is rotating. In addition, for some fraction of its orbit the light of its primary will prohibit data gathering.
To get around these issues the position and motion of the target must be known to exquisite accuracy so that the observatory motion can compensate or signal processing algorithms adapted to the residual motion. In particular, integration time should not exceed planetary motion (rotation and revolution) greater than one image pixel. If this isn’t possible the resolution will be degraded, perhaps to a degree where no algorithm can compensate.
Also, you really get only one shot at this since the spacecraft is unlikely to have a lot of fuel for maneuverability, and if the true motion of the target is unknown the required maneuvers will be unknown.
I think this is where they were implying that onboard AI could determine the required next position of the craft to capture the next pixels. I think one of the images in the NIAC paper shows the movement of a target system vs the sun’s disk. The planet’s motions and rate of spin are definitely complexities, although I have read other papers showing that rotation and orbital position can actually enhance the image.
As the data is transmitted back to Earth (about 6 days at 1000 AU) we would apply more powerful computers to process the data to build the image. Reality may make the image less good than the theory suggests, but at a minimum, the spatial data and spectral information would be very useful to characterize the state of the planet, even if the continents were a bit fuzzy. I wouldn’t be terribly upset if the pictures were better than Hubble’s imaging of Pluto, or similar in quality to the early 20th century’s images of Mars. A megapixel image with perfect mapping and perfect resolution is not going to be as good as a map generated from close orbit, but it is a lot better than a single pixel or few of an exoplanet that we have so far.
Look at the estimated signal integration times required for a static target. You would have to know the rotation period and inclination of the rotation axis and collect data every “day” to have enough to do the required integration. That’s a lot of maneuvering and fuel consumption, and risk of failure. Expect another imaging challenge due to the long integration time: weather and clouds that change daily.
Unfortunately we are nowhere near being able to do this type of observation, at any resolution. That said, the paper, if correct, provides valuable information about how imaging can be done. As I said, I just skimmed it, and I’m taking the calculations on faith.
Perhaps another great interstellar mission. I am impressed.
Could we do a smaller version, using one of the major planets of the solar system as a planetary gravitational lens? I know that David Kipping proposed that, and it certainly wouldn’t be as potent as the solar gravity lens. But it might be easier to reach.
I don’t see how. The focal length of the sun is about 550 AU while the focal length of Jupiter (the next best gravitational source) is about 5800 AU!
For more on this, see “Gravitational Lensing with Planets”:
https://centauri-dreams.org/2016/04/26/gravitational-lensing-with-planets/
Hi, Davis Kipping idea is called Terrascope was using the earth’s atmosphere as a telescope. Se this very good YouTube video about how it works;
Using Earth to See Across the Universe: The Terrascope with Dr. David Kipping.
https://www.youtube.com/watch?v=OjXN-SmHvC0
The more massive and smaller the object is, the closer the gravitational focus is. So, unfortunately, the Sun is the easiest object around the neighborhood for this
Here are two Centauri Dreams articles from 2019 on the Terrascope;
Planetary Lensing: Enter the ‘Terrascope’.
by PAUL GILSTER on AUGUST 12, 2019
https://centauri-dreams.org/2019/08/12/planetary-lensing-enter-the-terrascope/
The Terrascope: Challenges Going Forward.
by PAUL GILSTER on AUGUST 13, 2019
https://centauri-dreams.org/2019/08/13/the-terrascope-challenges-going-forward/
David Kipping suggest that the infrared would would work best along with microwaves. BREAKTHROUGH WATCH has been working on a new observing technique using a thermal infrared coronagraph to observe planets around Alpha Centauri’s planetary systems;
“Imaging potentially habitable exoplanets has presented a major technical challenge, since the starlight that reflects off them from their host stars is generally billions of times dimmer than the light coming to us directly from those stars. Resolving a small planet close to its star at a distance of several light years has been compared to spotting a moth circling a streetlamp dozens of miles away. To solve this problem, in 2016 Breakthrough Watch and ESO launched a collaboration to build a thermal infrared coronagraph, designed to block out most of the light coming from the star and optimized to capture the infrared light emitted by the warm surface of an orbiting planet.”
https://breakthroughinitiatives.org/news/32
Could this infrared coronagraph be used to block the light emitted from the bright earth in the one meter Terrascope? Could the refocused image after cancelling the earthlight also use a second infrared coronagraph to block the light from Alpha Centauri A or B to see the details on any planets found???
But for now what is needed is a CubeSat with a simple 100 mm lens sent out to the Hill radius or at about 1 million miles. The ASTERIA (Arcsecond Space Telescope Enabling Research in Astrophysics) would be a good model to work from with a near infrared chip. This would be a cheap test bed to see how well the idea of an infrared Terrascope would work…
One problem for the solar gravitational lens (SGL) is that a receiver must be close the ecliptic. Any effort to reach the area to observe the Alpha Centauri system would take huge amounts of energy to fly above or below the ecliptic plane that all the planets revolve around the sun. The Terrascope would be able to reach the same areas near earth with a simple ion engine. There are 12 to 20 nearby stars with exoplanets that are along the ecliptic plane or called the more conventional Zodiac.
These stars would be very easy to maneuver to with the ion engine to bring the Terrascope into the the correct position in the ecliptic
to see the stars thru the earth’s upper atmosphere. See chart below, the green line running across the chart is the ecliptic;
Location of stars with potentially habitable Exoplanets.
https://www.hpcf.upr.edu/~abel/phl/hec2/images/hec_starmap.png
The three most interesting; Trappist 1, Ross 128, Teegarden’s star are right on the ecliptic. Many more are not listed on this chart and are within 10 to 15 degrees of the north or south of the ecliptic. I have a hunch that something similar to the Kepler’s K2 orbit with the Terrascope facing earth would work…
How long would it take to do each of these projects and get results?
1. Solar Gravitational Lens (SGL): 30 to 50 years!
2. Terrascope: 3 to 5 years…
If nothing else, Terrascope would get the public excited about being able to see exoplanets in some detail instead of just a blip. It would also lend support to the SGL mission since the resolution would be much higher. Ignite the public’s imagination like UFOs did and you will have all the money you could possibly need…
The idea of making a lens with gravity won’t work since it breaks the laws of physics. We can’t make a telescope lens from warped gravity in empty space. Gravitational microlensing is detected as a increase in brightness of the star caused by an exoplanet passing in front of the star. The gravity concentrates the star light and makes it brighter. It only works one way when the exoplanet and star is distant from us, but our Sun’s gravity will distort both light of the star and exoplanet. so it doesn’t work both ways which is beside the point. I don’t think actual, optical lens can be made of warped space which is not the purpose of gravitational microlensing.
Hi Geoffrey Hillend
What are you reacting to? The paper uses the mass of the Sun to warp space and this has been discussed conceptually since at least the 1930’s.
Indeed. Which is why we talk about ‘Einstein rings’. Von Eshleman at Stanford was at work on pushing the equations much further half a century ago. And of course there’s the ground-breaking work of Claudio Maccone.
Sorry about my mistake. I did not read this paper carefully enough. I haven’t heard of the Einstein ring before and I should have looked that one up online first before jumping to a fast conclusion.
Would it be feasible to combine a gravity focus mission with an interstellar probe mission? Before launch an ideal planetary system could be chosen for gravitational lensing along with a destination star on opposite side of the sun. It would be interesting to see a study on the ideal instrumentation for each mission, and if they could be combined without exceeding mass constraints. Two birds could be had with the toss of a single stone.
Nat, one issue with this: for the interstellar probe “side” of the mission, you want the craft to be moving as rapidly as possible right from the get-go, like with laser-communicated acceleration beamed from earth orbit or from earth itself, à la Breakthrough Starshot. But for the gravity focus side of the mission, you presumably need enough maneuverability at 550 AU to keep the optical target behind you in focus, over the time necessary to collect enough photons. It seems like these are incompatible needs!
As with most things, this sounds like a really neat idea. However, the planning and feasibility studies alone (if approved at all) will likely be beyond my time left on this rock (i.e. 30-odd years). Figure in launch, getting into position and becoming operational – that will take it beyond my children’s time (70+ years (hopefully)) on this rock. We’re probably looking at about 100 years (or more) before we get data back…. which is fine and the planning and funding can accommodate that but does this not take us into the territory of “well what’s the point of sending out generation ships when we will have faster ships that will get to the destination way before them”… It could be we will have a different capability that allows the goals of this mission to be met way before the system ever becomes operational.
The “pixel” situation is the most serious issue, but I wonder if there is another way to solve it, taking a cue from the compound eyes of insects. To begin with, the cited amplification of 2E+11 is entrancing – that’s 28 orders of magnitude! If I take, say, Earth (absolute magnitude at -3.99 at 1 AU, 27.6 at 10 pc I think), then a similarly warm planet near us should have a negative magnitude. You shouldn’t need a Palomar telescope to get one pixel of light out of a planet like that, but just a tiny detector, with a sunshade flying somewhere in formation in front of it.
What if the telescope launched spreads into three or more fair-sized mother ships that collectively provide the power source, communications, and thrust, each of which can interrogate the tiny pixel observatories with lasers or lower-frequency links? The observatories would be like RFID chips, with no power except when a beam shines at them, and would need to be heard only by the mother ship doing the beaming. The beam would also provide light pressure to adjust their position, which the triangulated lightspeed delays would reveal.
I don’t know if you’d need electronics that functions natively at microwave-background temperature, or whether you could heat the pixel telescopes enough to work for the interval of their periodic interrogations.
I have to admit after reading through this post and the comments attached carefully to being quite confused now about the feasibility of doing an SGL mission in the near or medium term future. It’s a long way to 550 AU (that would be about 55 billion miles or nearly 75 light hours away I think). Surely this type of project i.e. to put a telescope of some sort at this location is decades or more away unless a huge propulsion breakthrough occurs so I have to agree with tesh and also including uncertainty about technical difficulties such as those Ron S. and others have mentioned. I look forward to any future posts on this subject.
There should be an update on the interesting ‘string of pearls’ payloads the team came up with in their Phase II report, so we’ll have more to work with as the Phase III effort continues.
This is the other big advantage of the David Kipping’s Terrascope, it is only 5 light seconds away instead of 75 light hours! The JWST would work because the earth sun angle at times is some 33 degrees but the scope can not be point at that position because of exposure to the sun’s rays will heat it up. What other telescopes are at the Sun-Earth L2 Lagrange point located about 1.5 million km from Earth or any other position at 1.5 million km? We have many spacecraft functioning at that distance with high speed data links. Close enough for a Starship repair…
List of objects at Lagrange points.
https://en.wikipedia.org/wiki/List_of_objects_at_Lagrange_points
L2
Present probes
Gaia and James Webb Space Telescope orbit around Sun-Earth L2
The ESA Gaia probe
The joint Russian-German high-energy astrophysics observatory Spektr-RG
The joint NASA, ESA and CSA James Webb Space Telescope (JWST)
Planned probes
The ESA Euclid mission, to better understand dark energy and dark matter by accurately measuring the acceleration of the universe.
The NASA Nancy Grace Roman Space Telescope (WFIRST)
The ESA PLATO mission, which will find and characterize rocky exoplanets.
The JAXA LiteBIRD mission.
The ESA ARIEL mission, which will observe the atmospheres of exoplanets.
The joint ESA-JAXA Comet Interceptor
The NASA Advanced Technology Large-Aperture Space Telescope, which would replace the Hubble Space Telescope.
The NASA Nancy Grace Roman Space Telescope (WFIRST) looks like it may be a good scope to see if the Terrascope would work. The ESA Euclid a visible to near-infrared space telescope to be launch in 2023 may actually be capable of using the earth’s atmosphere for super imaging exoplanets! It has a 1.2 meter mirror, but can the scope’s orbit bring the earth sun angle far enough to still keep it cool? Interesting…
Barnard’s Star is so fast…is it going to pass in front of any objects of interest so as to lens them for us?
Indeed, there is potentially a plethora of lensing stars out there relatively close by, each with its own set of potential target systems at their far side. The attraction of using a distant lensing sun instead of our own Sun is that it affords us the luxury of staying home while doing the relevant astronomy. However, gravscope performance degrades as one goes further out along the focal line. The performance drop-off in the case of a non-solar lensing star may be too severe. Only the maths will tell, and I fear that’s above my pay grade.
It’s not completely necessary to go all the way to 550 AU to start getting images, if multi craft are sent each spaced out equally and following the bending arc of the image light and communicating with each other. At 250 AU a 1 m mirror behaves as a 2 m mirror and it gets stronger much quicker at we approach the start of the focal line. If there are many craft communicating the shortish distance between them of say around 800 000 miles maximum via lasers a very high resolution image would be available quite quickly. The distance of communication again drops off quite fast as we approach the SFL.
Isn’t the Einstein ring the source of the massively increased resolving power? If so, do these separated telescopes see the ring at all until they reach the SGL? It seems to me that in extermis you are arguing that telescopes, at 1 AU, separated by the width of the sun, would be just as efficient as a single telescope at the SGL. I don’t see that.
What would the telescope see at 250AU? A partial Einstein ring? The same target?
Partial. You’ve probably seen the short arcs in astronomy pics, which are smears of large objects (e.g. galaxies) not precisely positioned behind the lens.
Being closer than 550 A.U. is not the same but there are important similarities. An exoplanet will produce a very very short arc in this instance. One resolvable target area on the exoplanet surface is approximately a point within that arc.
Clearly the light available is far less than that of the full ring and therefore the integration time will be far worse than shown in the paper, and that is already too long. I don’t believe that being closer than 550 A.U. would produce data of any value.
Although the Intergration time is greater there is plenty of time and in the end we get the image we wantake when we arrive at the SFL Even if the image data is small to start with we can still get some valuable information on the planet or maybe moon if there. Also if there are many mirrors there may be other planets around there that could be looked at.
If the many spacecraft transmit the image data towards a central collator probe it would have a resolving power of the sun’s diameter but only the sum of the collected image power of all the probe mirrors. So we have high resolution at the beginning and keep that resolving power as we move towards the 550 AU SFL but with increasing magnification. And yes each probe would have part of a eistein ring until they all reach the SFL.
Hello,
The gravitational focus of a small black hole, at what distance would it be?
I imagine a black hole with a mass like a planet. Like the supposed Planet X…
Best wishes, thanks
The focus of any small to moderate mass BH would certainly be closer. That isn’t useful since we don’t have one handy and the smaller diameter of the BH’s Einstein ring has less light gathering power. Although if there is no accretion disk there is less resolution impairment in comparison to using the sun.
In any case, there is no good reason to believe that naturally formed sub-solar mass BH exist, and there is no evidence of a solar mass BH nearby.
Very interesting! Thanks!
Of course, it’s like a theoretical exercise probably of fiction of mine.
I imagine if it could be with a very small radius and very, very small focal length.
So, some focal point of the BH could be aligned with the Sun. And this point could be…
A focal point with two lenses working at once. A point where the Sun’s focus is closer, approached, and then a little useful, but a view very limited.
Good wishes!