It’s hard to imagine what the field of exoplanet discovery will look like in a hundred years. Just as difficult as it is to imagine what might happen if we do get to a ‘singularity’ in machine intelligence beyond which we humans can’t venture. Will the study of other stellar systems become largely a matter of computers analyzing data acquired by AI, with human operators standing by only in case of equipment failure? Or will the human eye for pattern and detail so evident in many current citizen science projects always be needed to help us piece together what the machines find?
I wonder this when I read about the effort going into teasing new data out of older observations, as we saw recently in VASCO, a project to study old astronomical photographic plates looking for possible technosignatures. And I suspect we’ll always need human/machine collaboration to draw maximum knowledge out of our data. Today let’s look at how useful software tools are illuminating what we’ve already learned about an exceedingly interesting and relatively close planetary system.
Sometimes it becomes necessary to begin writing about something by carefully explaining what it is not. In this case, I’m talking about the planetary system e Eridani, otherwise known as 82 Eridani, and it’s important to add that this is not the system known as Epsilon Eridani. The latter, interesting in its own right, is nearby (10.5 light years) and in fact is the third closest individual star system visible to the naked eye. The former, our subject today, is 20 light years out, a G-class dwarf with several confirmed planets. In the southern hemisphere Gould star catalogs, compiled in the late 19th Century, it is listed as the 82nd star in the constellation Eridanus.
This is potentially confusing enough that I’m going to use 82 Eridani rather than e Eridani in this article, which will look at an interesting way to study exoplanet systems that are close by, and one that offers useful new insights into what may be found in the 82 Eridani system that we have yet to discover. We already know about two planets, now confirmed, that were found through radial velocity data, and the same data suggest another. As many as six planets may exist here based on recent analysis by Fabo Feng (University of Hertfordshire) and colleagues in a 2017 paper.
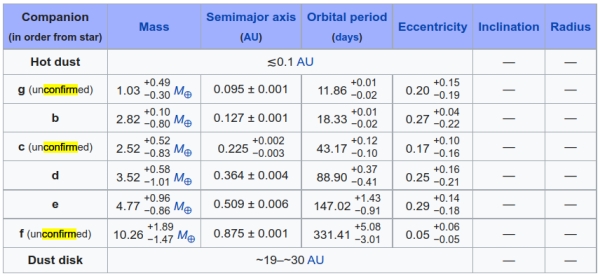
Image: This table shows what we currently know about the planetary system at 82 Eridani, including evidence for a dust disk. As we’re about to see, a hypothetical seventh planet turns up in the work we discuss below. Credit: Wikimedia Commons.
In a new paper in the Astronomical Journal, Ritvik Basant (University of Arizona) and colleagues go to work on the planetary architecture of 82 Eridani with a software package called DYNAMITE (developed by co-author Daniel Apai) that folds information specific to this system into a broader analysis incorporating what the authors call ‘exoplanet demographics.’ At stake here is this question: If an additional planet exists in a given system, what can we say about the probability distributions of its orbit, its eccentricity, its likely size? Let me quote from the paper:
To answer this question, DYNAMITE uses the robust trends identified in the Kepler exoplanet demographics data (orbital period distribution, planet-size distribution, etc., based on the ?2400 exoplanets that form the Kepler population) with specific data for a given single exoplanet system (detected planets and constraints on their orbits and sizes). Based on this information, DYNAMITE uses a Monte Carlo approach to map the likelihood of different planetary architectures, also considering the orbital dynamical stability and allowing for the freedom of statistical model choice.
I’m going into the weeds here because this package has already shown its worth. Back in 2020, Apai and co-author Jeremy Dietrich used DYNAMITE on 45 transiting systems discovered by TESS (Transiting Exoplanet Survey Satellite) to make predictions about undiscovered planets. Their work showed in multiple instances that an already discovered planet, if initially hidden from the software, would be retrieved by DYNAMITE, a test the software also passed when applied to the system at TOI-174, where more than one planet was removed and the probability of additional planets was noted in the software.
The accomplishments of DYNAMITE can be further examined in the paper, but I’ll mention its utility in the Tau Ceti system and its prediction of a habitable zone planet there, as well as interesting work on the K2-138 system, where it made what turns out to have been accurate predictions on two planets. So this seems to be a robust package, drawing heavily on existing data on planetary populations – it works best with the typical rather than the outlier, in other words, a fact to keep in mind before we extrapolate too freely.
Exoplanet science is all about tugging facts out of challenging data, as has been the case since the detection of 51 Pegasi b or, for that matter, the pulsar planets at PSR 1257+12. Continually refining our techniques through ever more sophisticated equipment sharpens radial velocity and transit detections, but we’re also learning how the right algorithms can be applied to the data we generate to suggest new targets for study. As our equipment improves, our algorithms are continually tuned up.
What we have so far for 82 Eridani shows the method at work in a system where our knowledge of several planet candidates is uncertain. DYNAMITE generates hypotheses exploring possible combinations of planet candidates. Each of these hypotheses produces predictions, and as it turns out, all four hypotheses produced for 82 Eridani result in planetary orbits that are quite similar. The authors also draw on a new DYNAMITE module that uses a statistical approach to explore possible surface temperatures. So this is a wide ranging look at the system, and they consider the work an “exploratory assessment” only, until more constraining data become available.
It will be interesting indeed to see how accurately this assessment describes what we will one day find with improved observational techniques. Beginning with the assumption of a system consisting of only the three known planets, DYNAMITE provides further support for the earlier work that predicted three more potential worlds (no information from the 2017 study, mentioned above, was used as input for the software). The parameters for the three candidate planets turn out to be in good agreement with the results of Fabo Feng and team. If all six planets, confirmed and unconfirmed, are used as input, DYNAMITE then predicts one additional planet in the habitable zone.
Here the software is suggestive in relation to the orbital eccentricity of these worlds:
From our eccentricity analysis, we find that if e Eridani is a three-planet system with planets b, d, and e, then the combined mean eccentricity for the system to be stable is ?0.05. If the system is a six-planet system instead, then the combined mean eccentricity for the system to be stable is of an order ?0.026. In either case, we find that the eccentricity of each planet should be significantly lower than the value fitted to the RV data, as also proposed by Feng et al. (2017a).
As the planetary system’s stability necessitates a lower-than-reported eccentricity for the planets, our analysis is based on this assumption. If better constraints on the eccentricities become available in future, then our analysis could be repeated again with the updated values.
So this is a rolling process, with the DYNAMITE results seeming to support seven planets at this star, including one additional candidate in the habitable zone, joining the previously predicted 82 Eridani f there. Indeed, the habitable zone around this star is wide enough, and the inner planetary system likely to be complex enough, to raise 82 Eridani higher on the list of planetary systems we will want to examine for life, using future direct imaging via space-based observatories and terrestrial extremely large telescopes. That new habitable zone planet candidate, by the way, would likely be a mini-Neptune rather than a terrestrial world based on the DYNAMITE results.
It’s interesting to see that Guillem Anglada-Escudé, the astronomer behind the discovery of Proxima Centauri b, worked with exoplanet hunter Paul Butler to develop an algorithm called TERRA to filter noise and sharpen radial velocity analysis. It was this algorithm that turned up the evidence for the three additional candidates at 82 Eridani in Feng and team’s 2017 paper that played into the work using DYNAMITE.
So we have three known planets at 82 Eridani, three more suggested by the TERRA analysis of the existing RV data and strengthened by the DYNAMITE results, and now a possible seventh world with an orbital period of 549-733 days in the habitable zone. Again, the new worlds here are planet candidates at this point and await further observation and analysis. The latter will give us one day the data that will tighten algorithms like these still further, giving us better options to distinguish between probabilities and decide which of them merit precious telescope time.
The paper is Basant et al, “An Integrative Analysis of the Rich Planetary System of the Nearby Star e Eridani: Ideal Targets for Exoplanet Imaging and Biosignature Searches,” Astronomical Journal Vol. 164, No. 1 (16 June 2022) 12 (full text). If you want to dig further into the background, the Feng et al. paper is “Evidence for at least three planet candidates orbiting HD?20794,” Astronomy & Astrophysics Vol. 605 (September 2017) A 103 (abstract).



The first 4 planets (g,b,c,d) in the table fit a normalized Titus-Bode Law sequence, although it rapidly falls apart with the 5th and 6th (e,f) orbits being too small.
They also are not a bad fit for a Fibonacci sequence:
Fibonacci 82 Eridani AU Normalized (to planet g)
1 0.095 1.0
1 0.127 1.3
2 0.225 2.4
3 0.364 3.8
5 0.509 5.4
8 0.875 9.2
Probably a coincidence and no doubt there is a sequence that will match the orbital distances quite well by chance.
This is where algorithms can also be useful – quickly testing the known planetary systems against a library of mathematical sequences to see if there are any sequences that match far more frequently than probability would suggest.
AI currently sits tantalizingly close to being able to do creative work. It can extract underlying math and physics from data sets and has long since been able to drive a robotic lab system to plan and execute genomic experiments to minimize cost (and eliminate bench work tedium). While humans still have the edge in scientific creativity, whether that will be true in a century may be in doubt. Some disciplines will succumb quickly, others not for a long time.
I doubt any of us will be around a century from now, but if I was, I would prefer AIs to be partners able to quickly determine if ideas are valid, or to produce analyses to inform ideas, as they are sometimes depicted in SciFi tv and movies. In the trivial case above, I added the planetary orbits to a spreadsheet, added the Fibonacci sequence, used Wikipedia to give me the Titus-Bode formula, then did some calculations to see that the Fibonacci sequence fit best. It would have been so much faster if I had been able to ask my AI to “Extract the orbits in the table I am viewing, and tell show me if they give a good match to a Fibonacci sequence or Titus-Bode Law.” After the results were shown ask: “Show any known math sequences that better fit the data.” “Does this best fit sequence apply to other planetary systems?” and so on. Much of this is not particularly “intelligent”, just a master algorithm in the old symbolic AI tradition with the “knowledge” to extract the required data from many sources and do the tedious calculations. There was once some idea to make clean data sets publicly available in a database (Google even had a basic platform), but this seems to have died. A smart Wikipedia that was able to find and extract data and information, do calculations, and compose reports would be the least intelligent system I would expect 100 years from now.
Using a spreadsheet, the confirmed and predicted 6 planets have orbital distributions that follow an exponential equation of the form:
orbital radius AU = a*e^(b*n) where n = planet number [1..6]
The R value for a linear trendline between the actual (and predicted) orbits of the planets and the exponential fit = 0.997
The Fibonacci data when plotted against the actual data as a scatterplot has a linear trendline with an R = 1.0 – a perfect fit, suggesting that adjusting the normalization values would provide a very good fit.
Is this in any way telling us something about the author’s model in a more basic form?
Here is a good article on DYNAMITE’s workings.
How astronomers are searching for exoplanets using 4 simple variables.
New mathematical technique enables astronomers to predict the whereabouts of missing worlds around nearby stars.
https://astronomy.com/news/2020/11/how-astronomers-are-searching-for-exoplanets-using-4-simple-variables
DYNAMITE’s main web site:
Alien Earths
https://eos-nexus.org/
https://eos-nexus.org/dynamite/
Here is a article on some of the alternates to the Titus-Bode Law sequence from the late 1920s–1930. The very interesting of idea of using the concept of quantum superposition relating the Quantized Nature of Orbital Systems.
https://www.science.org/doi/pdf/10.1126/science.71.1846.513
A better image of the original article:
https://www.science.org/cms/10.1126/science.71.1846.513/asset/d3881ab5-70e0-4767-9c80-1ef2c77d12cd/assets/science.71.1846.513.fp.png
The theory by Victor Goldschdimt of the law of harmonic relations of distances for planets and satellites, could we see how well it matches up with the results of DYNAMITE’s Undetected Planets in Multi-planet Systems?
X Marks the Region.
https://aasnova.org/2020/10/20/x-marks-the-region/
Hidden Worlds: Dynamical Architecture Predictions of Undetected Planets in Multi-planet Systems and Applications to TESS Systems.
https://arxiv.org/abs/2007.06745
A full 3 page article that includes A.E. Caswell theory; “The mean distance of the planets from the Sun are proportional to the squares of simple integral numbers.”
https://articles.adsabs.harvard.edu//full/1931PA…..39…75W/0000075.000.html
Bad link this should work better;
https://articles.adsabs.harvard.edu/full/1931PA…..39…75W
Bode’s and similar empirical laws – Wylie, C. C.
The arxiv.org preprint, the “X Marks the Region” article and the astronomy.com articles are good complements to the OP.
The DYNAMITE Python software package is available on GitHub to be used by interested parties.
It seems to me [naively?] that their model is a nice integration of components that outputs probability density functions for planets that, as Ron S. says:
. Note they did test the Solar System excluding Mars, and the model predicted a planet in Mars’ orbit. A 1995 paper by Chambers on multi-plamnet stability using the Hill radius is one method they use to predict planetary orbits.
[I don’t see any mathematical connection with resonance orbits, so I don’t know if this just conveniently appears in the PDF values, or could be used as a tweak to sharpen the PDF around an orbit.]
What is interesting is that the model could be used to test the concept of fitting planetary orbital distributions to simpler mathematical sequences [e.g. Titus-Bode Law, Fibonacci, exponential function, etc, etc], albeit tweaked with the impact of planetary masses. This seems like it could be a citizen science project if some initial sampled systems could be tested with confirmed and predicted possible planets.
[I do note that the authors state that our system is a bit of an outlier when compared to the discovered systems’ PDF of the planets and their orbits of multi-planet systems, although their DYNAMITE model does work by predicting a planet where an excluded Mars is.].
Using the Volk and Malhotra paper “Dynamical instabilities in systems of multiple short-period planets are likely driven by secular chaos: a case study of Kepler-102”, figure 3 shows a peak period ratio between adjacent planets of the Kepler 102 system as around 1.8.
The radius = cube_root(period^2)
This finding seems to be one of the 2 stability criteria (the other being Hill radius separation) that DYNAMITE uses to place the predicted stable planets. While planetary masses are important for the Hill radius separation, the Chamber’s papers show that stability is reasonably ensured if the multiple of Hill radius separation is large enough. This acts as a constraint on the possible orbital period ratios, which for Kepler 102 peaks.
If this ratio is fixed across all the planets in a system, and a converging value across most planetary systems, then an approximate exponential fit between the orbital radius of planets for systems with multiple planets in the same plane and with very low eccentricities then we can expect an exponential distribution of planetary semi-major axes with some deviations due to other formation factors, masses, resonance dynamics, etc.
As the DYNAMITE package uses the statistical data of planetary orbits from known transiting planets, this relationship might be locked in as part of the calculation to predict possible undiscovered planets.
Therefore the sequence of most common radii spacing is exponential. [Q.E.D. ?]
Here is a recent version of the concept of using Quantum Mechanics for planetary orbits in our solar system and exoplanetary systems.
Planetary orbits in solar and extrasolar systems.
Rub?i?, Antun; Rub?i?, Jasna
Source / Izvornik: Fizika A, 2010, 19, 133 – 144
Conclusion.
“We applied our model of quantization of orbits in the solar system on newly discovered extrasolar planetary systems. We confirmed that the square law for the distribution of orbits deduced from observational orbital parameters in solar system
(Eq. (1) and/or Eq. (2)) also holds for the extrasolar planetary systems. Both integers, the orbital number n and the spacing number k, can easily be determined from observed periods and semi-major axes of planets in systems considered. All this may be useful in the classification of orbits. Thus third root of the period divided by some small integer number n needs to be nearly constant for all planets in the system. Then, n is the number of orbit. We emphasize that the square law of orbits defines only the architecture of the planetary system, but details
can only be determined by using observational parameters of some real objects belonging to the system considered. When the possible set of orbits is defined on the basis of occupied orbits, then one can anticipate which empty orbits could
contain unobserved planets.
For example, the 55 Cnc planets e, b, c, f, and d are, according to our analysis, located at orbits 1, 2, 3, 5 and 14. Eight orbits at n = 4, 6,..13 are empty. The first thought is that at orbit 4 could be a small yet undetected planet. Moreover, the authors in Ref. [6] presume that in the gap between periods of 260 days to 13 yr
several planets could exist and probably maintain dynamical stability.
In the HD 10180 planetary system, the first five orbits are occupied by the planets b, c, d, e, and f. The last planet h with relatively large mass is at the orbit 14. But at orbit 9 there is the planet g. Similarity with 55 Cnc system is impressive.
The procedure outlined above has also been applied to the origin of the Moon. Namely, in the terrestrial planets, the orbit 7 is empty and is located between Mars and Ceres. We have put forward a hypothesis that the Moon originated at that
orbit and later on migrated to be captured by the Earth [1e]. The argument for such an assertion is that definite mass and volume of the Moon are expected when compared with the same quantities of all terrestrial planets.
We hope that determination of possible orbits according to square law could be a guide in the search for extrasolar planetary systems.”
https://repozitorij.pmf.unizg.hr/islandora/object/pmf%3A7119/datastream/FILE0/view
Quantization and Discretization at Large Scales; Kindle Edition
Free with Kindle Unlimited!
As I understand this work it is quite different to our historical approach to predicting new planets in our own system. Orbital data in the solar system was not consistent with the planetary complement. The deviation of observation and calculation was used to predict the possible orbits and physical parameters of Uranus, Pluto and Vulcan. The latter, of course, turned out instead to be a limitation of the existing theory of gravitation.
The resolution of the data for other stellar systems is, at least so far, insufficient to do the same kind of prediction for undiscovered planets. What I glean from this article is that they assume the system is stable (which is reasonable) and calculate the phase space of planetary orbits and physical parameters that would not disturb the assumed long term stability of the system, and that do not cause observable deviations of the orbits of the already discovered exoplanets.
This does not assure that these planets exist, only that they could exist. As they say, further observation is needed to see if they are indeed there.
This is a strange system – an old, low metallicity star with three large solid? planets in close orbits, plus a potential dust disk further out.
I wonder if those three inner worlds aren’t the cores of Neptune sized worlds that migrated inwards during their formation and have slowly evaporated since then. The putative dust disk can be the condensed remains of the evaporated material.
I wonder how accurate the data on Wikipedia is.
Take planet f, r = .875 AU. Kepler’s Third Law, for a star the mass of the sun, gives a period of 0.81849 earth years, or 298.95 earth days, NOT 331.41 days. That means the star has a mass of 81.37% of our sun.
The wiki article gives M = 0.70 M sol, implying a year of 357.3 days.
The difference in mass between 0.70 and 0.8137 is non-trivial.
???
The paper referenced by Wikipedia shows they used a stellar mass of 0.813Msol, which is more or less what you have calculated. The mass in the wiki article and the mass used by the paper have come from different sources, that probably explains the discrepancy.
So it has two potential sub-Neptunian gas dwarf planets in its HZ? That doesn’t sound promising for life – they would have pushed out any Earth-like world in that HZ.
Moons? Double planets?
Looking at the proper motion and radial velocity components of 82 erandini it must have been a lot closer to the sun in the past.
Orbital resonances.
There was a post some time ago about the number of orbital resonances. I cannot recall if it was for an exoplanet system such as Trappist-1, or for planets and moons in our system.
It did get me thinking about this as a driver. The Volk and Mahotra paper Dynamical instabilities in systems of multiple short-period planets are likely driven by secular chaos: a case study of
Kepler-102 on the probability distribution (figure 5) of exoplanet distances between pairs of adjacent orbits peaking around 1.8 that is used in the DYNAMITE package implies a resonance of 9/5 that is fairly universal.
While this works for adjacent pairs, if resonances should extend over a wider range of orbits, for example, planets 1 and 3, 2 & 5, etc, is there some optimum arrangement of resonances that can be made to fit more of a system? The optimization has the lowest integers for the numerator (orbital period of the outer planet) and denominator (orbital period of the inner planet).
For example, in a 3-planet system, the orbital multipliers would not be 1.8 between each adjacent pair as this creates a 3.24 (81/25) resonance between planets 1 and 3. Optimization might be for the difference of 1.8 between planets 1 and 2 (9/5) resonance, and a 3.33 (10/3) between planets 1 and 3, leaving a 1.85 (close to 1.83 = 11/6) multiple between planets 2 and 3. Planetary mass would be a factor in which pairs of planet resonances would be most dominant so that if planet 3 was a Jupiter-class planet, it would have the most influence on the resonances that best work for planets 1 and 2.
A brute force algorithm could offer a set of optimized planetary orbits with resonances across as much of a planetary system as possible, with the largest mass planet being the “anchor” to align the orbits and maximize the resonances.
A Monte Carlo approach using different numbers of planets in a system with differing arrangements of planet mass should show a distribution of planet orbital period multiples that match the distribution observed by Volk and Malhotra.
Does any of this make any sense, or is this excessive “numerology” to force-fit resonances rather like Kepler s Platonic Solids Model of the Solar System?
Excessive numerology? Perhaps, but it depends on what it is you’re trying to accomplish. The Titius-Bode law and its legion of improvements by later investigators have some value. However, it is really little more than a heuristic when you need a rapid analysis of a system, say, on the back of a napkin.
Reliance on those simple models was understandable centuries ago when it simply wasn’t possible to model a system, even though Newton’s theory of gravitation was quite adequate to run a model through many millions of years to test for stability and to locate “holes” where system stability is unlikely to be disturbed. Of course it couldn’t be done because the computation capacity did not exist.
With a better theory of gravitation and ample computation capacity, these simple laws are in many respects merely articles of curiosity. At best they are good for initial hypothesis generation. Since the system can be well modelled over eons — only phase space since all gravitational systems are chaotic — a precise analysis will pay not the slightest attention to these simple models: they are not needed and can be terribly misleading.
Nevertheless, it is interesting that n-body gravitational system can so often be roughly analyzed and predictions facilitated with a few elementary calculations. That’s part of the beauty of phase space in chaos theory.
Phase space and quantum mechanics – phase space and quantum gravity are very similar, but we the earth and everything else are just waves. The most fundamental particle the electron is just a phase locked cavity, a trapped photon standing wave. Over billion of years systems will gravitate to this pattern on a celestial scale as we see in redshift quantization.
So you reject the particle-wave duality of quantum mechanics? If so, how do you explain the experiments that demonstrate the point-like particle nature of photons and electrons?
Yes, the point is the waves of the electrons going at the speed of light. See R. C. Jennison; https://www.lenr-forum.com/attachment/1195-jennison2-pdf
I have no idea what any of this means.
I agree with what you are saying. However, simple models that can provide useful answers with few computations can be very useful for predicting unknowns, such as planets that have yet to be discovered in systems with confirmed planets. Running large numbers of calculations on limited computational resources is of value if those calculations provide statistically correct answers.
I have just run a calculation to find all the lowest resonances with integer values to fill in the possible high probability period multiples of exoplanets found by Volk and Malhotra. (Maximum integer as a numerator = 29.)
A spot check suggests that our system is an anomaly. There could be a planet between Mercury and Venus, as well as 2 planets between Mars and Jupiter. Either the model is wrong, or is missing something important.
This is my output of possible integer periods as resonances that fit V&M’s exoplanet multiples where the probability >= 0.5. This includes the period multiple ranges [1.5…1.9] and [2.1…2.2]
The table shows the period multiple values for the discovered inter periods and teh calculated orbital radius multiples as a result.
This can be used as a lookup table to chain orbital periods and semi-major radii through resonances to find best fits to known orbits and to infer orbits where there is no planet or moon.
Period Mult. Resonance Radius mult.
1.500 3/2 1.310
1.526 29/19 1.326
1.529 26/17 1.327
1.533 23/15 1.330
1.538 20/13 1.333
1.545 17/11 1.337
1.556 14/9 1.343
1.563 25/16 1.347
1.571 11/7 1.352
1.583 19/12 1.358
1.588 27/17 1.361
1.600 8/5 1.368
1.611 29/18 1.374
1.615 21/13 1.377
1.625 13/8 1.382
1.636 18/11 1.389
1.643 23/14 1.392
1.647 28/17 1.395
1.667 5/3 1.406
1.688 27/16 1.417
1.692 22/13 1.420
1.700 17/10 1.424
1.706 29/17 1.428
1.714 12/7 1.432
1.727 19/11 1.440
1.733 26/15 1.443
1.750 7/4 1.452
1.769 23/13 1.463
1.778 16/9 1.468
1.786 25/14 1.472
1.800 9/5 1.480
1.813 29/16 1.487
1.818 20/11 1.490
1.833 11/6 1.498
1.846 24/13 1.505
1.857 13/7 1.511
1.867 28/15 1.516
1.875 15/8 1.521
1.889 17/9 1.528
1.900 19/10 1.534
2.100 21/10 1.640
2.111 19/9 1.646
2.125 17/8 1.653
2.143 15/7 1.662
2.154 28/13 1.668
2.167 13/6 1.674
2.182 24/11 1.682
2.200 11/5 1.692
The CD post on orbital resonances:
TOI-178: Six Transiting Planets & a Unique Resonance Chain
From the posted table, it does strike me that the eccentricities are large compared to the Solar System (only Mercury in the inner system is comparable), although the error bars are large too.
This seems concerning, as such large eccentricities imply that the 2 inner planets, b and g, would have g’s apoapsis and b’s periapsis that allows a collision. This also applies to confirmed planets d, e.
The Table from Wikipedia appears to be derived from the Feng et al paper Evidence for at least three planet candidates orbiting HD20794 (Table 4) which has these very wide error bars for the eccentricities. I have to wonder if the large range of eccentricities and their averages are an artifact of the authors’ modeling approach rather than reality. [Their model is too difficult for me to follow.]