Aerospace engineer Wes Kelly continues his investigations into gravitational lensing with a deep dive into what it will take to use the phenomenon to construct a close-up image of an exoplanet. For continuity, he leads off with the last few paragraphs of Part I, which then segue into the practicalities of flying a mission like JPL’s Solar Gravitational Lens concept, and the difficulties of extracting a workable image from the maze of lensed photons. The bending of light in a gravitational field may offer our best chance to see surface features like continents and seasonal change on a world around another star. The question to be resolved: Just how does General Relativity make this possible?

by Wes Kelly

Conclusion of Part I

At this point, having one’s hands on an all-around deflection angle for light at the edges of a “spherical lens” of about 700,000 kilometers radius (or b equal to the radius of the sun r_S), if it were an objective lens of a corresponding telescope, what would be the value of the focal length for this telescopic component expressed in astronomical units?

The angle of 700,000 km solar radius observed from 1 AU, gives an arcsine of 0.26809 degrees. This is consistent with the rule of thumb solar diameter estimate of ~0.5 degrees.

Expressed in still another way, solar radius from this arcsine measure is 965 arc seconds. When the solar disc itself is observed to be about 1.75 arc seconds in radius, that’s where you will find the focus for this objective lens.

If we take the ratio of 965 to 1.75, we obtain a value 551.5. In other words, a focal point for the relativistic effect at 551.5 AU’s out. Thus, the General Relativity effect implies that light bent by the sun’s gravity near its surface radius is focused about 550 AUs out from the sun. And like the protagonist of Moliere’s 16th century comedy play, as I run off to tell everyone I know, I discover a feeling akin to, “For more than forty years I have been speaking prose while knowing nothing of it.”

This could be a primary lens for a very unwieldy telescope. True, but not unwieldy in all manners. When we consider the magnification power of a telescope system, we speak of the focal length of the objective lens over that for an eye piece or sensor lens focal length. And habitually one might assume it is enclosed in a canister – as most telescopes sold over the counter at hobby stars are. But it is not always necessary or to any advantage. Consider the largest ground-based optical reflectors, or the JWST and radio telescopes. Their objective focal lengths extend through the open air or space. The JWST focal length is 131.4 meters or taller than its Ariane V launch system. Its collected light reaches sensors through a succession of ricochets in its instrumentation package, but not through. a cylindrical conduit extending out from the reflector any significant distance to the front. [Note: The Jupiter deflection case mentioned above would make the focal length 100x longer.]

Continued Discussion

(Tables, Figures and References for Parts I and II are sequential).

In contrast with a 130-meter objective lens focal length, with 550 AU, any focal length for a conventionally manufactured “eyepiece” lens optical system of any size would have enormous magnification or light gathering potential. Were it a lens of 1 or 10 or 100 meter focal length at the instrument end of the telescope, with the “Oort Cloud radius sized” objective lens focal length (550 x 1.5xe8 meters = 8.2 x 10e8 meters) it would not matter much so far as interstellar mapping would be concerned now. We should add as well that the magnification is in terms of area rather than diameter or radius. In effect magnification is multiplication of projected surface area or surface light.

Given the above, issues that remain to be addressed related to the field of view.

1. The spherical lens (the sun) is a light source itself, which needs to be blocked out with a coronagraph on board the SGL spacecraft.

2. The signal obtained from the star (but especially the planet!) is “convoluted” by passage around the perimeter of the solar lens. This must be undone by a deconvolution process.

3. In application for examining an exoplanet in orbit around another star, the fix on the star must be either adjusted to center on the related planetary target or else the planet’s data must be extracted from an enormous extraneous data package.

On issue 1, there are many coronagraph techniques already applied in telescopes for blocking solar or stellar light sources. The Nancy Roman Space Telescope device when launched will be the state of the art and likely to influence SGL coronagraph design. For issue 2, it would be interesting to see a simple illustrative example (e.g., a sphere with a simple pattern such as broad colored latitudinal and longitudinal bands alternating in some patterns… a yellow or green smiley face?), transformed and then converted back. On issue 3, however, I believe that discussion below will provide more immediate insights.

Figure-6 As noted in [7], a meter class telescope with a coronagraph to block solar light is placed In the strong interference region of the solar gravitational lens (SGL) and is capable of imaging an exoplanet at a distance of up to 30 parsecs with a few 10-km scale resolution on its surface. The picture shows results of a simulation of the effects of the SGL on an Earth-like exoplanet image.

Left: Original RGB (red, green, blue) image with a 1024 x 1024 pixel array.

Center: Image blurred by the SGL, sampled at an SNR (signal to noise ratio) of 103 per color channel or overall SNR of 3 x 130.

Right: Result of image deconvolution.

In Reference 7 by Turyshev et al., with Figure-7, potential benefits of an SGL telescope are illustrated with a targeted planet similar to the Earth within a range of 100 light years. What follows is a reference point which we would like to examine as well; in this case, with a specific range (10 parsecs) to illustrate engineering and operational questions, concerns or trades. In archives, see also [ref. A12].

Figure-7 Contrast of benefits illustration with planet observed with an orbital plane in the line of sight of the GLT.

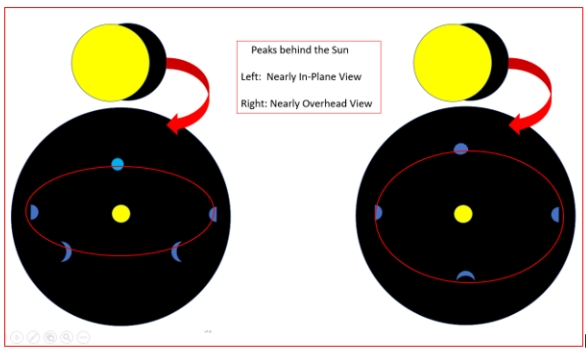
Figure-8 Observation of a target planet with an orbital plane inclined to the line of GLT line of sight.

Left side, with perpendicular to the orbital plane tipped forward, we can observe crescent phases similar to the planets orbiting the sun interior to the Earth, but at low angles, the illuminated exoplanet face is not illuminated. On the aft side of the sun it is in full phase, but perhaps experiencing significant glare. On the right side, with higher inclination, the exoplanet appears as a cat’s eye above the center point; below, as a crescent rotated at a right angle to its path.

What to Do about Slew?

As for deploying a telescope out into the Oort Cloud out to ~550 AUs: This seems explicable and feasible with a combination of conventional propulsion and orbital mechanics taken to a higher state of the art, nuclear thermal, nuclear fusion electric or thermal, sized based on constraints such as mass, mission duration, infrastructure and finance. It is assumed here, by this aerospace engineer, that trajectory, propulsion, navigation and guidance issues of deployment with resources not yet available but will be with larger spacecraft assembled and tested in the future. However, operational issues of this baseline or reference mission, I would still like to explore. In pursuit of this, we will add a reference target (perhaps the first of an enlarging set), an exoplanet similar to the earth in a solar system similar to ours at a viewing distance used to set stellar absolute magnitudes, a distance of ten parsecs.

Now if a stellar system were ten parsecs away or 32.26 light years off, the maximum radial offset of an Earth-like planet from a Sol like star (1 AU) would be 0.1 arc seconds. Hence, the Earth analog would be in the “nominal” field of view (FOV) but the FOV would encompass a radius of 175 AUs – If the center of the nominal FOV can be considered the center of the target star. The stellar absolute magnitude measure distance (10 parsecs ) is a middle distance for this exercise and a parsec (3.23 light years), also basic to astronomy, could be considered a minimum just below Alpha Centauri distance (4.3 light years).

However, FOV behind the sun used for now, might be misleading or unclear in these circumstances. Because it is not clear to me how much of the blocked celestial sphere is transferred back via the gravity lens phenomenon. In this analysis, without full understanding of how the coronagraph or convolutions will work, I am unsure whether there is any control over what the steradian field behind the sun will be; whether it can be entirely controlled. Focusing on the star could provide all the 175 AU radius in the field of view, or some fraction thereof. But if centering on a planetary target can limit the wasted scan area, I highly recommend such.

For argument’s sake, of this celestial “blockage” region, it could range from the infinitesimal to the whole. The image obtained might be treated akin to a point source from which we might extract image data somewhat akin to extracting the spectrum of a similar un-dimensioned source. Or there might be several different deconvolution methods which provide options. But the aspect that concerns me here is how one searches for a point source in this so-called FOV, more characterized by the blockage of the sun’s angular width. The FOV might be described as an area within an FOB, a field of blockage. Whether discerned directly without need of a deconvolution – or not – at ten parsec distance the field of “blockage” (FOB?) would include a radius of 175.5 AUs in the 17.5 arcsecond maximum field of view.

The diameter of a G2V sun like ours is about 0.01 AU and a terrestrial planet like our own is 0.01 of that. And then what kind of transformation or convolution would be required to take the information from the other side and convert it back into an image? An image we would recognize as a planet with continents, oceans and clouds. Not knowing for sure, I suspected that if the position of the target planet were known, it would make more sense to focus the telescope on it rather than the star itself. On the other hand, if obtaining a coronagraphic blocking of the star required centering on the star, and capturing the planet required processing the thick ring around the star, then the total amount of data processing could become enormous – as the following table shows.

In terms of terrestrial planet viewed area vs. that of the 1 AU radius region and the 175 AU radius encompassing the entire celestial pane blocked by the sun, the ratios are 1 to 500 million and 168 billion respectively. Depending on the resolution sought for the planetary analysis ( e.g., 10 kilometer features distinguishable), then data bits characterizing individual “squares” of smaller dimensions must be processed. For present purposes, we can select ten kilometers for illustration.

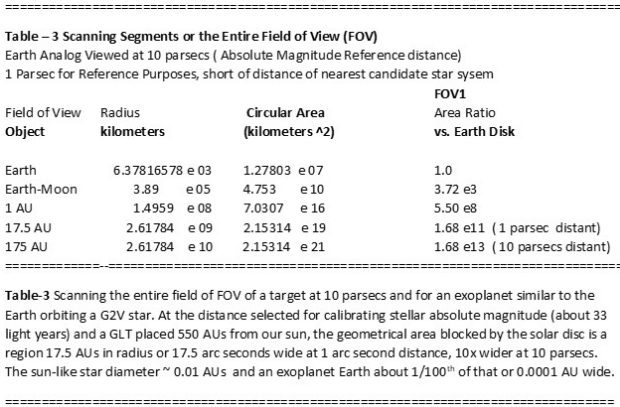
Table-3 Scanning the entire field of FOV of a target at 10 parsecs and for an exoplanet similar to the Earth orbiting a G2V star. At the distance selected for calibrating stellar absolute magnitude (about 33 light years) and a GLT placed 550 AUs from our sun, the geometrical area blocked by the solar disc is a region 17.5 AUs in radius or 17.5 arc seconds wide at 1 arc second distance, 10x wider at 10 parsecs. The sun-like star diameter ~ 0.01 AUs and an exoplanet Earth about 1/100th of that or 0.0001 AU wide.

As the NIAC Phase II Report and AIAA journal article [7 and 8] indicate, targeted resolution objectives are on the order of 10 kilometers, indicative of sampling cells of lower dimensions. A one-kilometer-wide sample cell we select for sake of argument. However, with each observed cell, the GLT telescope instrument suite will include 3 -5 color band sweeps (e.g., ultraviolet, blue, yellow, red, infra-red) which would include intensity levels. A spectrometer could also seek evidence of discrete spectral lines or molecular bands. So, for each square kilometer scanned, there could be considerable binary coded data for the telemetry link. More than one data-bit for sure associated with each polygon of space scanned by the SGL telescope. If each polygon has a location defined in a 2-dimensional grid, then that point likely has two 32 or 64-bit position assignments; then each color filter has an intensity. In addition, if spectral lines are tracked another databit code will be assigned to that point as well.

Processing the FOV indiscriminately with focus on the star is like searching for a needle (or data) in a haystack. Tracking the planet itself could eliminate orders of magnitude of excess data processing. On the other hand, slewing at 550 AU circular orbit entails 40,000 km magnitude oscillations over a year to follow the target, distances equivalent to a tenth of Earth-Moon separation, but an expenditure of propulsive resources. Consequently, this would become at least one resource trade between data handling and maneuverability. One possible solution would be multiple telescopes formation flying over “seasonal” tracking points a quarter of orbital revolution apart in the projected orbital track.

The scenario for deploying the telescope assumes considerable outbound velocity accumulated in the form of continuous low thrust acceleration. Consequently, on station a very large radial velocity will remain. Remarkably, at 550 AU distance, circular orbit velocities are still over a kilometer per second ( e.g., Earth orbital about 29.7 km/sec over square root of 550, about 1.27 km/sec). With the Earth-based example at 10 parsecs and the requirement to cover 40,000 km back and forth within about 6 months, the corresponding constant velocity would be 0.0025 km/sec to hold the alignment. This type of slewing would work better with a more rapidly orbiting exoplanet located in the HZ of a red dwarf. But the M star case would require more frequent reverses of direction. Significantly, were we to do this exercise for a target at 1 parsec such as the Alpha Centauri stars, the oscillations would be ten times larger (400,000 km) or about the distance to the moon.

Additionally, the rotation rate about the planetary axis could be star synchronous or, as with the Earth or Mars, much faster than the orbital revolution. There could be moons in its near vicinity. All these are natural considerations for a habitable zone exoplanet survey. And reasons that features on the exoplanet surface could become blurred. Other cases would generate different requirements, no doubt. And all this will affect how long it will take to process square kilometer data sets into each of their relevant maps.

Beside stellar glare, galactic background needs to be considered too. A dark field behind the target star would be preferable as well, achieving a higher signal to noise ratio. It would be a shame if threshold levels for observing a planet vs. magnified stellar backgrounds could not be assessed prior to flight. A potential problem making out the planet against the background would make a planetary ephemeris important; linkage to home base guide telescopes directing the GLT pointing, where in a sense the GLT will be blind. We have discussed just an Earth analog so far, but HZ targets at cooler K and M stars as well as hotter F main sequence stars could possess eye-opener properties too.

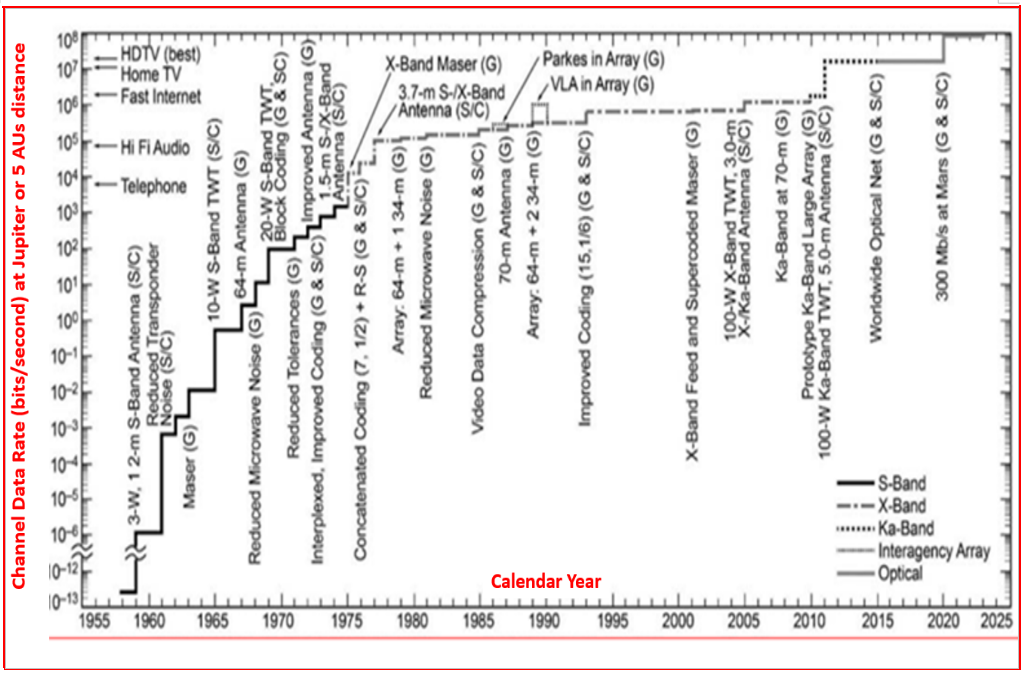
Several decades ago, during an undergraduate satellite design project I participated as the communications engineer – and then space navigation assignments called on putting on that hat again. An interesting experience each time and I found some overall equations that formulated relations among distance, signal to noise thresholds, signal rates and power required to stay in touch at both ends, spacecraft and the Deep Space Network. Unfortunately, I lost our first team’s final report in a flood, not of information like that discussed, but of tropical storm water. But it is not necessary to reconstruct the methods found then. At this date there is now an old literature base for communications with spacecraft situated in deep space, thanks to publications of the Jet Propulsion Laboratory, illustrative examples such as Voyager and other Jupiter bound spacecraft, even earlier spacecraft examined as if they were beaming from there and received with network capabilities of a given epoch (see Figure 9).

Figure-9 Figure-9 A diagram from Ref. 5 pegs down one end of the trade issues, chronological increases in data rates obtained from spacecraft in Jupiter vicinity. Reception is associated with 5.2 AU distance from the sun (varying with the Earth) vs. the 550 AUs or more anticipated for the GLT. On one axis, acquisition data rates are shown. For each spacecraft that sets out on these Jovian missions (some, of course, actually did not), a liftoff limit on power or data rate can be assumed for the spacecraft or observatory. Once launched, most of the growth was likely at the Earth based part of the communication link.

In comparison with attenuation of signals from the Jovian system at 5.2 AU for the various systems shown in the Figure-9 JPL diagram, signals 100x further out will be decreased in strength to ~1/10,000th or less with movement beyond 550 AU. Consequently, data rates shown in the diagram for various extent technologies will be dropped by a factor of 1/10,000th or 1.0 e-04 as well.

Depending on when such an SGL space observatory will be launched, some technologies will improve data transmission rates or storage capacities with respect to mass density or power required. Other technologies likely will not experience similar trends. For example, it is unclear what new Deep Space Network type tracking facilities will be employed in support of the SGL mission. However, if the data load is driven by a full scan of the equivalent of the solar angular area or FOV, the spacecraft system requirements for data storage and transmission are increased enormously.

On the other hand, as shown, slewing from the stellar focal point to a planetary position will require propellant resources and attitude control increases over those for the stellar fix. Even at 550 AU, there is a 1.28 km/sec characteristic circular orbit velocity. And depending on time of flight to outpost station delivery, in coast the spacecraft can be considered on an extremely hyperbolic heliocentric path. Consequently, fixed on a target planet, low thrust would be required without planet tracking even to maintain stellar focus.

My own quick assessment is that narrow field of view scanning in the planetary vicinity as it tracks around the star in some arbitrary orbital plane is the better procedure. The actual orbital plane’s normal could be inclined by some angle to the line of sight (See Figure 8). Hence, a circular path would be perceived as an elliptical projection; more complex if actually eccentric to a considerable fraction. But with a mean likelihood of 45-degree inclination and circular orbit, half phases would appear at greatest stellar elongation. Near the line of sight, a cat’s-eye would appear behind the star and a crescent in front with lowest elongation and greatest glare. With zero inclination of the planet, we are bound to learn much about its northern hemisphere and much less about its south, depending on its rotational axis alignment.

Now if a stellar system were ten parsecs away or about 33 light years off, the maximum radial offset of an Earth-like planet from a Sol like star (1 AU) would be 0.1 arc seconds. Hence, the Earth analog would be in the “nominal” field of view (FOV) but the FOV would encompass a radius of 17.5 AUs – If the center of the nominal FOV can be considered the center of the target star.

FOV, used for now, might be misleading in these circumstances. Because it is not clear to me how much of the blocked celestial sphere is transferred back via the gravity lens phenomenon.

For argument’s sake, of this celestial “blockage” region, it could range from the infinitesimal to the whole. The image obtained might be treated akin to a point source from which we might extract image data somewhat akin to extracting the spectrum of a similar un-dimensioned source. So the aspect that confuses me here is how one searches for a point source in this so-called FOV, more characterized by the blockage of the sun’s angular width. The FOV might be described as an area within an FOB, a field of blockage.

In this situation, there would have to be some fore-knowledge of where the target planet should be. You would need a tracker observatory probably closer to Terra home. You still need a means to locate a body orbiting an object about a hundredth of an AU in diameter and in turn a planet about 1/10,000 of an AU wide. To relay information from a stellar observatory not experiencing this occultation by the sun to 550 AUs out, the lag would be about 3.174 days based on the speed of light.

And then, presumably, the observatory would need to slew toward this planetary target from the reference point of the stellar primary – or perhaps even the center of mass in a binary system. Alpha Centauri could be such an example.

A Mission for One Star System and Exoplanet or More?

Additional trade issues to consider are related to completion of observation and characterization of one planetary system. Perhaps there is more than one planet (or a moon) in a target system to study. But there is also the issue of observing more than one planetary system. Minimal angular separation of two “good” candidate systems in the celestial sphere would have to be weighed against the “excellence” of an isolated stellar system with no potential for a phase II mission elsewhere, say within one degree of circular arc. Faced with such a dilemma I would hope that observing the isolated system over years until system deactivation will be well worthwhile.

At this writing we are aware of about 5000 exoplanets with attributable features, providing a range of reasons for continued or closer observation. Like the other design issues described above, eventually there will be the dilemma of which exoplanet or planets to select.

In terms of steradians, the whole celestial sphere has an area of 4 ? units. With some experimentation I discover that it is possible to determine the equidistant position of any number of stars – which can illustrate the dilemma of deciding how to deploy the SGL Telescope. The celestial arc A between equally spaced stars of a given number n can be described with the answer in radians convertible to degrees. Once n equals or exceeds 3, the equidistant points can be viewed as vertices to equilateral and equiangular spherical triangles of given arc segments, the latter the significant parameter. The total of 5000 exoplanets is not distributed with an equal spacing, but there is an element of likelihood with the fractional degree separation overall. And, of course, a smaller selection of select exoplanet systems will have wider individual separations overall, but perhaps a few will be less than a degree apart. For the case of ten parsec distant planetary system we noted that a traverse to cover 17.5 AUs encompassed about 400,000 kilometers at 550 AU. A one degree traverse is 205 times as large but it does not have tracking determined maneuver velocity requirements.

It is likely that by some set of selected parameters, several exoplanets can be selected for further scrutiny. However, if several parameters are involved and a couple of candidates or alternates can be identified in proximity, it is possible that two close star systems could outscore focus on one, even if it generally acknowledged the best, but located on the wrong side of the sky for total mission benefit.

Consequently, the mission analysis could become more complicated as time passes with a larger and larger selection of nearby systems identified with one or more planets.

What would the parameters tend to be to warrant such a trade? Even if there is no evidence of life, an exoplanet of exceptional nature could transcend parameters associated with habitable zone parameters or signs of life. And for examination of signs of life, our knowledge will have to exceed such identifications as diameter, albedo and placement in a habitable zone: atmospheric composition, nature of hydrosphere, traces of processes similar to terrestrial ones… Cost benefit issues too of propulsion and maneuver to survey two planets would need to have an identifiable threshold against the additional spacecraft weight budget for propulsion. If the two candidate systems are far apart, then the choice might be easier in a way if it requires launching two distinct missions.

Whether going for two exoplanets separated by a degree or more is worthwhile, is difficult to ascertain at this early stage. But the determination will depend on establishing criteria for a trade. To first order it will depend on how outstanding signs of life might be within a future database of exoplanets. And if not clear, which parameters of an exoplanet or a maneuverable spacecraft should be considered and with what weight. Reflecting on an earlier orbital application proposal, Arthur C. Clarke suggested geosynchronous orbit for a single communications relay station, elaborated as a call center with humans at switchboards. Instead, we have numerous geosats with no one aboard. It could be that SGL spacecraft will proliferate similarly and for several purposes. At the very least, we can be thankful to be able to consider such possibilities, coming from a time decades back when exoplanets were simply considered fantasy like Spock’s planet – or more locally – Lescarbault’s and Le Verrier’s Vulcan.

References for Part I and Part II

1.) Pais, Abraham, Subtle is the Lord … The Science and Life of Albert Einstein, Oxford University Press, 1982.

2.) https://www.stsci.edu/jwst/science-execution/observing-schedules

3.) Vallado, David A., Fundamentals of Astrodynamics and Applications, 2nd edition, Appendix D4, Space Technology Library, 2001.

4.) Moulton, Forest Ray, An Introduction to Celestial Mechanics, 2nd Edition, Dover, 1914 Text.

5.) Taylor, Jim et al. Deep Space Communications, online at https://descanso.jpl.nasa.gov/monograph/series13_chapter.html

6.) Wali, Kamshwar, C., Chandra – A Biography of S. Chandrasekhar, U. of Chicago Press, 1984.

7.) Turyshev et al., ”Direct Multipixel Imaging and Spectroscopy of an Exoplanet with a Solar Gravity Lens Mission,” Final Report, NASA Innovative Advanced, Concepts (NIAC) Phase II.

8.) Helvajian, H. et al., “Mission Architecture to Reach and Operate at the Focal Region of the Solar Gravitational Lens,” Journal of Spacecraft and Rockets, American Institute of Aeronautics and Astronautics (AIAA), February 2023, on line pre-print.

9.) Xu, Ya et al., ”Solar oblateness and Mercury’s perihelion precession”, MNRAS, 415, 3335-3343, 2011.

A1.) Archives: In the Days before Centauri Dreams… An Essay by WDK (centauri-dreams.org)

A2.) Archives: A Mission Architecture for the Solar Gravity Lens (centauri-dreams.org)

Here in Houston, the University of Houston, Clear Lake Physics and Astronomy Club had a recent meeting when the sky was obscured by clouds and the president had asked in advance, just in case of such circumstances, would I have any presentation I could give that night. There were some other ones that had grown all out of control, so I decided to start on a fresh topic. This article grew out of the evening presentation and consequently, it is dedicated to the club and its members.

WDK
13 April 23