Centauri Dreams
Imagining and Planning Interstellar Exploration
SunVoyager: A Fast Fusion Mission Beyond the Heliosphere
1000 AU makes a fine target for our next push past the heliosphere, keeping in mind that good science is to be had all along the way. Thus if we took 100 years to get to 1000 AU (and at Voyager speeds it would be a lot longer than that), we would still be gathering solid data about the Kuiper Belt, the heliosphere itself and its interactions with the interstellar medium, the nature and disposition of interstellar dust, and the plasma environment any future interstellar craft will have to pass through.
We don’t have to get there fast to produce useful results, in other words, but it sure would help. The Thousand Astronomical Unit mission (TAU) was examined by NASA in the 1980s using nuclear electric propulsion technologies, one specification being the need to reach the target distance within 50 years. It’s interesting to me – and Kelvin Long discusses this in a new paper we’ll examine in the next few posts – that a large part of the science case for TAU was stellar parallax, for classical measurements at Earth – Sun distance allow only coarse-grained estimates of stellar distances. We’d like to increase the baseline of our space-based interferometer, and the way to do that is to reach beyond the system.
Gravitational lensing wasn’t on the mind of mission planners in the 1980s, although the concept was being examined as a long-range possibility by von Eshleman at Stanford as early as 1979, with intense follow-up scrutiny by Italian space scientist Claudio Maccone. Today reaching the 550 AU distance where gravitational lensing effects enable observation of exoplanets is much on the mind of Slava Turyshev and team at JPL, whose refined mission concept is aimed at the upcoming heliophysics decadal. We’ve examined this Solar Gravity Lens mission on various occasions in these pages, as well as JHU/APL’s Interstellar Probe design, whose long-range goal is 1000 AU.

What Kelvin Long does in his recently published paper is to examine a deep space probe he calls SunVoyager. Long (Interstellar Research Centre, Stellar Engines Ltd) sees three primary science objectives here, the first being observing the nearest stars and their planets both through transit methods as well as gravitational lensing. A second objective along the way is the flyby of a dwarf planet that has yet to be visited, while the third is possible imaging of interstellar objects like 2I/Borisov and ‘Oumuamua. Driven by fusion, the craft would reach 1000 AU in a scant four years.
Image: The Interstellar Research Centre’s Kelvin Long, here pictured on a visit to JPL.
This is a multi-layered mission, and I note that the concept involves the use of small ‘sub-probes’, evidently deployed along the route of flight, to make flybys of a dwarf planet or an interstellar object of interest, each of these (and ten are included in the mission) to have a maximum mass of 0.5 tons. That’s a lot of mass, about which more in a moment. Secondary objectives involve measurements of the charged particle and dust composition of the interstellar medium, astrometry (presumably in the service of exoplanet study) and, interestingly, SETI, here involving detection of possible power and propulsion emission signatures as opposed to beacons in deep space.
Bur back to those sub-probes, which by now may have rung a bell. Active for decades in the British Interplanetary Society, Long has edited its long-lived journal and is deeply conversant with the Daedalus starship concept that grew out of BIS work in the 1970s. Daedalus was a fusion starship with an initial mass of 54,000 tons using inertial confinement methods to ignite a deuterium/helium-3 mixture. SunVoyager comes nowhere near that size – nor would it travel more than a fraction of the Daedalus journey to Barnard’s Star, but you can see that Long is purposely exploring long-range prospects that may be enabled by our eventual solution of fusion propulsion.
Those fortunate enough to travel in Iceland will know SunVoyager as the name of a sculpture by the sea in central Reykjavik, one that Long describes as “an ode to the sun or a dream boat that represents the promise of undiscovered territory and a dream of hope, progress, and freedom.” As with Daedalus, the concept relies on breakthroughs in inertial confinement fusion (ICF), in this case via optical laser beam, and in an illustration of serendipity, the paper comes out close to the time when the US National Ignition Facility announced its breakthrough in achieving energy breakeven, meaning the experiment produced more energy from fusion than the laser energy used to drive it.

Image: The Sun Voyager (Sólfarið) is a large steel sculpture of a ship, located on the road Sæbraut, by the seaside of central Reykjavík. The work of sculptor Jón Gunnar Árnason, SunVoyager is one of the most visited sights in Iceland’s capitol, where people gather daily to gaze at the sun reflecting in the stainless steel of this remarkable monument. Credit: Guide to Iceland.
Long’s work involves a numerical design tool called HeliosX, described as “a system integrated programming design tool written in Fortran 95 for the purpose of calculating spacecraft mission profile and propulsion performance for inertial confinement fusion driven designs.” As a counterpart to this paper, Long writes up the background and use of HeliosX in the current issue of Acta Astronautica (citation below). The SunVoyager paper contemplates a mission launched decades from now. Long acknowledges the magnitude of the problems that remain to be solved with ICF for this to happen, notwithstanding the encouraging news from the NIF.
…a capsule of fusion fuel, typically hydrogen and helium isotopes, must be compressed to high density and high temperature, and this must be sustained for a minimum period of time. One of the methods to achieve this is by using high-powered laser beams to fire at a capsule in a spherical arrangement of individual beam lines. The lasers will mass ablate the surface of the capsule and through momentum exchange will cause the material to travel inward under spherical compression. This must be done smoothly however, and any significant perturbations from spherical symmetry during the implosion will lead to hydrodynamic instabilities that can reduce the implosion efficiency. Indeed, the interaction of a laser beam with a high-temperature plasma involves much complex physics, and this is the reason why programs on Earth have found it so difficult.
Working through our evolving deep space mission designs is a fascinating exercise, which is why I took the time years ago to painstakingly copy the original Daedalus report from an academic library – I kept the Xerox machine humming in those days. Daedalus, a two-stage vehicle, used electron beams fired at capsules of deuterium and helium-3, the resulting plasma directed by powerful magnetic fields. Long invokes as well NASA’s studies of a concept called Vista, which he has also written about in his book Deep Space Propulsion: A Roadmap to Interstellar Flight (Springer, 2011). This was a design proposal for taking a 100-ton payload to Mars in 50 days using a deuterium and tritium fuel capsule ignited by laser. Long explains:
The capsule design was to utilize an indirect drive method, and so a smoother implosion symmetry may give rise to a higher burn fraction of 0.476. This is where the capsule is contained within a radiation cavity called a Hohlraum and where the lasers heat up the internal surface layer of the cavity to create a radiation bath around the capsule; as opposed to direct laser impingement onto the capsule surface and the associated mass ablation through the direct drive approach.
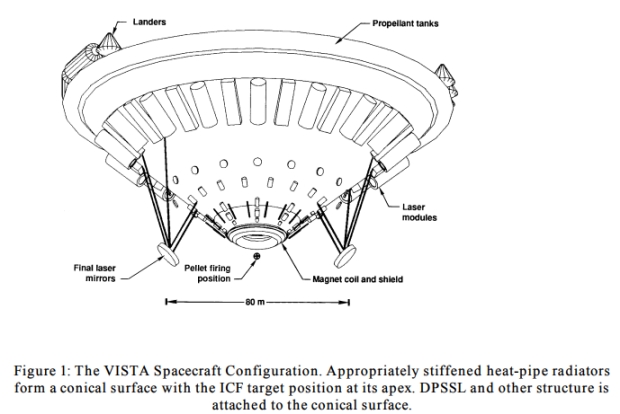
Image: Few images of the Vista design are available. I’ve swiped this one from a presentation made by C. D. Orth to the NASA Advanced Propulsion Workshop in Fusion Propulsion in 2000, though it dates back all the way to the 1980s. Credit: NASA.
SunVoyager would, the author comments, likely use a similar capsule design, although the paper doesn’t address the details. Vista feeds into Long’s thinking in another way: You’ll notice the unusual shape of the spacecraft in the image above. Coming out of work by Rod Hyde and others in the 1980s, Vista was designed to deal with early ICF propulsion concepts that produced a large neutron and x-ray radiation flux, sufficient to prove lethal to the crew. The conical design was thus an attempt to minimize the exposure of the structure to this flux, with a useful gain in jet efficiency of the thrust chamber. SunVoyager is designed around a similar conical propulsion system. The author proceeds to make predictions for the performance of SunVoyager by using calculations growing out of the Vista design as modeled in the HeliosX software.
In the tradition of Daedalus and Vista, SunVoyager explores ICF propulsion in the context of current understanding of fusion. I want to talk more about this concept next week, noting for now that a fast mission to 1000 AU –SunVoyager would reach that distance in less than four years – would take us into an entirely new level of outer system exploration, although the timing of such a mission remains hostage to our ability to conquer ICF and generate the needed energies to actualize it in comparatively small spacecraft systems. This doesn’t even get into the matter of producing the required fuel, another issue that will parallel those 1970s Daedalus papers and push us to the limits of the possible.
The paper is Long, “Sunvoyager: Interstellar Precursor Probe Mission Concept Driven by Inertial Confinement Fusion Propulsion,” Journal of Spacecraft and Rockets 2 January 2023 (full text). The paper on HeliosX is Long, “Development of the HeliosX Mission Analysis Code for Advanced ICF Space Propulsion,” Acta Astronautica, Vol. 202, Jan. 2023, pp. 157–173 (abstract). See also Hyde, “Laser-fusion rocket for interplanetary propulsion,” International Astronautical Federation conference, Budapest, Hungary, 10 Oct 1983 (abstract).

Gathering the Evidence for Life on Enceladus
With a proposal for an Enceladus Orbilander mission in the works at the Johns Hopkins Applied Physics Laboratory, I continue to mull over the prospects for investigating this interesting moon. Something is producing methane in the ocean under the Enceladus ice shell, analyzed in a 2021 paper from Antonin Affholder (now at the University of Arizona) and colleagues, using Cassini data from passages through the plumes erupting from the southern polar regions. The scientists produced mathematical models and used a Bayesian analysis to weigh the probabilities that the methane is being created by life or through abiotic processes.
The result: The plume data are consistent with both possibilities, although it’s interesting, based on what we know about hydrothermal chemistry on earth, that the amount of methane is higher than would be expected through any abiotic explanation. So we can’t rule out the possibility of some kind of microorganisms under the ice on Enceladus, and clearly need data from a future mission to make the call. I won’t go any further into the 2021 paper (citation below) other than to note that the authors believe their methods may be useful for dealing with future chemical data from exoplanets of a wide variety, and not just icy worlds with an ocean beneath a surface shell.
Now a new paper has been published in The Planetary Science Journal, authored by the same team and addressing the potential of such a future mission. A saltwater ocean outgassing methane is an ideal astrobiological target, and one useful result of the new analysis is that it would not take a landing on Enceladus itself to probe whether or not life exists there. Says co-author Régis Ferrière (University of Arizona):
“Clearly, sending a robot crawling through ice cracks and deep-diving down to the seafloor would not be easy. By simulating the data that a more prepared and advanced orbiting spacecraft would gather from just the plumes alone, our team has now shown that this approach would be enough to confidently determine whether or not there is life within Enceladus’ ocean without actually having to probe the depths of the moon. This is a thrilling perspective.”
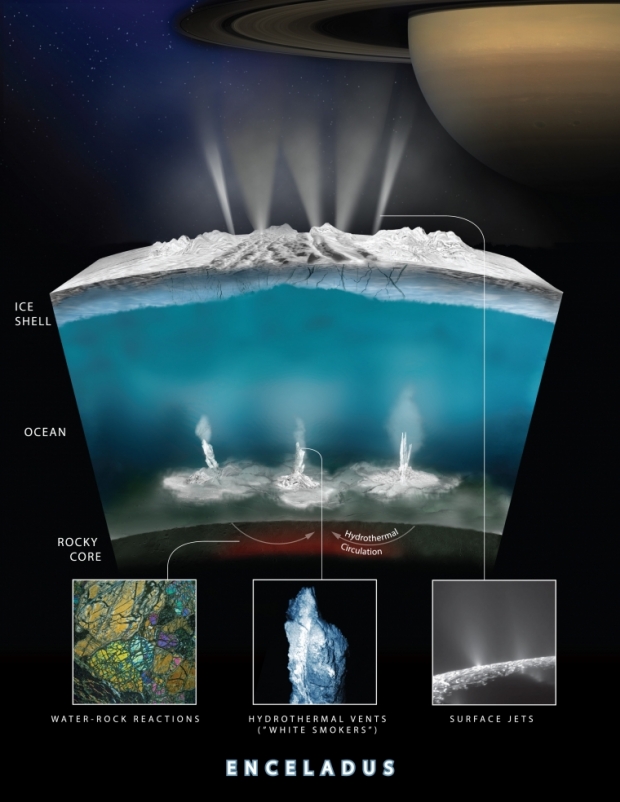
Image: This graphic depicts how scientists believe water interacts with rock at the bottom of Enceladus’ ocean to create hydrothermal vent systems. These same chimney-like vents are found along tectonic plate borders in Earth’s oceans, approximately 7000 feet below the surface. Credit: NASA/JPL-Caltech/Southwest Research Institute.
Microbes on Earth – methanogens – find ways to thrive around hydrothermal vents deep below the surface of the oceans, in regions deprived of sunlight but rich in the energy stored in chemical compounds. Indeed, life around ‘white smoker’ vents is rich and not limited to microbes, with dihydrogen and carbon dioxide as an energy source in a process that releases methane as a byproduct. The researchers hypothesize that similar processes are at work on Enceladus, calculating the possible total mass of life there, and the likelihood that cells from that life might be ejected by the plumes.
The team’s model produces a small and sparse biosphere, one amounting to no more than the biomass of a single whale in the moon’s ocean. That’s an interesting finding in itself in contrast to some earlier studies, and it contrasts strongly with the size of the biosphere around Earth’s hydrothermal vents. But the quantity is sufficient to produce enough organic molecules that a future spacecraft could detect them by flying through the plumes. The mission would require multiple plume flybys.
Actual cells are unlikely to be found in the plumes, but detected organic molecules including particular amino acids would support the idea of active biology. Even so, we are probably going to be left without a definitive answer, adds Ferrière:
“Considering that according to the calculations, any life present on Enceladus would be extremely sparse, there still is a good chance that we’ll never find enough organic molecules in the plumes to unambiguously conclude that it is there. So, rather than focusing on the question of how much is enough to prove that life is there, we asked, ‘What is the maximum amount of organic material that could be present in the absence of life?'”
An Enceladus orbiter, in other words, would produce strong evidence of life if its measurements were above the threshold identified here. Back to the JHU/APL Enceladus Orbilander, thoroughly described in a concept study available online. The mission includes both orbital operations as well as a landing on the surface, with thirteen science instruments aboard to probe for life in both venues. The mission would measure pH, temperature, salinity and availability of nutrients in the ocean as well as making radar and seismic measurements to probe the structure of the ice crust.

Image: Artist’s impression of the conceptual Enceladus Orbilander spacecraft on Enceladus’ surface. Credit: Johns Hopkins APL.
Here the chances of finding cell material are much higher than in purely orbital operations, where survival through the outgassing process of plume creation seems unlikely. The lander would target a flat space free of boulders at the moon’s south pole with the aim of collecting plume materials that have fallen back to the surface. The team points out that the largest particles would not reach altitudes high enough for sampling from orbit, making the lander our best chance for a definitive answer.
The paper, indeed, points to this conclusion:
…cell-like abiotic structures (abiotic biomorphs) that may form in hydrothermal environments could cause a high risk of a false positive… Assuming that cells can be identified unambiguously…, we find that the volume of plume material that needs to be collected to confidently sample at least one cell might require a large number of fly-throughs in the plume, or using a lander to collect plume particles falling on Enceladus’s surface (e.g., the Enceladus Orbilander; MacKenzie et al. 2021).
The paper is Affholder et al., “Putative Methanogenic Biosphere in Enceladus’s Deep Ocean: Biomass, Productivity, and Implications for Detection,” Planetary Science Journal Vol. 3, No. 12 (13 December 2022), 270 (full text). The paper on methane on Enceladus is Affholder at al., “Bayesian analysis of Enceladus’s plume data to assess methanogenesis,” Nature Astronomy 5 (07 June 2021), 805-814 (abstract).

Chasing nomadic worlds: Opening up the space between the stars
Ongoing projects like JHU/APL’s Interstellar Probe pose the question of just how we define an ‘interstellar’ journey. Does reaching the local interstellar medium outside the heliosphere qualify? JPL thinks so, which is why when you check on the latest news from the Voyagers, you see references to the Voyager Interstellar Mission. Andreas Hein and team, however, think there is a lot more to be said about targets between here and the nearest star. With the assistance of colleagues Manasvi Lingam and Marshall Eubanks, Andreas lays out targets as exotic as ‘rogue planets’ and brown dwarfs and ponders the implications for mission design. The author is Executive Director and Director Technical Programs of the UK-based not-for-profit Initiative for Interstellar Studies (i4is), where he is coordinating and contributing to research on diverse topics such as missions to interstellar objects, laser sail probes, self-replicating spacecraft, and world ships. He is also an associate professor of space systems engineering at the University of Luxembourg’s Interdisciplinary Center for Security, Reliability, and Trust (SnT). Dr. Hein obtained his Bachelor’s and Master’s degree in aerospace engineering from the Technical University of Munich and conducted his PhD research on space systems engineering there and at MIT. He has published over 70 articles in peer-reviewed international journals and conferences. For his research, Andreas has received the Exemplary Systems Engineering Doctoral Dissertation Award and the Willy Messerschmitt Award.
by Andreas Hein

If you think about our galaxy as a vast ocean, then the stars are like islands in that ocean, with vast distances between them. We think of these islands as oases where the interesting stuff happens. Planets form, liquid water accumulates, and life might have emerged in these oases. Until now, interstellar travel has been primarily thought in terms of dealing with how we can cross the distances between these islands and visit them . This is epitomized by studies such as Project Daedalus and most recently Breakthrough Starshot, Project Daedalus aiming at reaching Barnard’s star and Breakthrough Starshot at Proxima Centauri. But what if this thinking about interstellar travel has missed a crucial target until now? In this article, we will show that there are amazing things hidden in the ocean itself – the space between the stars.
It is frequently believed that the space between the stars is empty, although this stance is incorrect in several ways, as we shall elucidate. The interstellar community is firmly grounded in this belief. It is predominantly focused on missions to other star systems and if we talk about precursors such as the Interstellar Probe, it is about the exploration of the interstellar medium (ISM), the incredibly thin gas long known to fill the spaces between the stars, and also features of the interaction between the ISM and our solar wind, such as the heliosheath, or with its interaction with microscopic physical objects or phenomena linked to our solar system. However, no larger objects between the stars are taken into account.

Image: Imaginary scenario of an advanced SunDiver-type solar sail flying past a gas-giant nomadic world which was discovered at a surprisingly close distance of 1000 astronomical units in 2030 by the LSST. The subsequently launched SunDiver probes spotted several potentially life-bearing moons orbiting it. (Nomadic world image: European Southern Observatory; SunDivers: Xplore Inc.; Composition: Andreas Hein).
Today, we know that the space between the stars is not empty but is populated by a plethora of objects. It is full of larger flotsam and smaller “driftwood” of various types and different sizes, ejected by the myriads of islands or possibly formed independently of them. Each of them might hold clues to what its island of origin looks like, its composition, formation, and structure. As driftwood, it might carry additional material. Organic molecules, biosignatures, etc. might provide us with insights into the prevalence of the building blocks of life, and life itself. Most excitingly, some important discoveries have been made within the last decade which show the possibilities that could be obtained by their exploration
In our recent paper (Lingam, M., Hein, A.M., Eubanks, M. “Chasing Nomadic Worlds: A New Class of Deep Space Missions”), we develop a heuristic for estimating how many of those objects exist between the stars and, in addition, we explore which of these objects we could reach. What unfolds is a fascinating landscape of objects – driftwood and flotsom – which reside inside the darkness between the stars and how we could shed light on them. We thereby introduce a new class of deep space missions.
Let’s start with the smallest compound objects between the stars (individual molecules would be the smallest objects). Instead of driftwood, it would be better to talk about sawdust. Meet interstellar dust. Interstellar dust is tiny, around one micrometer in diameter, and the Stardust probe has recently collected a few grains of it (Wetphal et al., 2014). It turns out that it is fairly challenging to distinguish between interstellar dust and interplanetary dust but we have now captured such dust grains in space for the first time and returned them to Earth.
The existence of interstellar dust is well-known, however, the existence of larger objects has only been hypothesized for a long time. The arrival of 1I/’Oumuamua in 2017 in our solar system changed that; 1I is the first known piece of driftwood cast up on the beaches of our solar system. We now know that these larger objects, some of them stranger than anything we have seen, are roaming interstellar space. There is still an ongoing debate on the nature of 1I/’Oumuamua (Bannister et al., 2019; Jewitt & Seligman, 2022). While ‘Oumuamua was likely a few hundred meters in size (about the size of a skyscraper), larger objects also exist. 2I/Borisov, the second known piece of interstellar driftwood, was larger, almost a kilometer in size. In contrast to ‘Oumuamua, it showed similarities to Oort Cloud objects (de León et al., 2019). The Project Lyra team we are part of has authored numerous papers on how we can reach such interstellar objects, even on their way out of the solar system, for example, in Hein et al. (2022).
Now comes the big driftwood – the interstellar flotsam. Think of the massive rafts of tree trunks and debris that float away from some rivers during floods. We know from gravitational lensing studies that there are gas planet-sized objects flying on their lonely trajectories through the void. Such planets, unbound to a host star, are called rogue planets, free-floating planets, nomads, unbound, or wandering planets. They have been discovered using a technique called gravitational microlensing. Planets have enough gravity to “bend” the light coming from stars in the background, focusing the light, brightening the background star, and enabling the detection even of unbound planets.
Until now, about two hundred of these planets (we will call them nomadic worlds in the following) have been discovered through microlensing. These detections favor the more massive bodies, and so far objects with a large mass (Jupiter-sized down to a few Earth masses) have been detected. Although our observational techniques do not yet allow us to discover smaller nomadic worlds (the smallest ones we have discovered are a few times heavier than the Earth), it is highly likely that smaller objects, say between the size of the Earth and Borisov, exist. Fig. 1 provides an overview of these different objects and how their radius is correlated with the average distance between them according to our order of magnitude estimates. Note that microlensing is good at detecting planets at large interstellar distances, even ones thousands of light years away, but it is very inefficient (millions of stars are observed repeatedly to find one microlensing event), and with current technology is not likely to detect the relative handful of objects closest to the Sun.
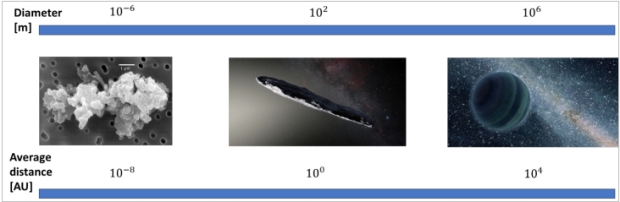
Fig. 1: Order of magnitude estimates for the radius and average distance of objects in interstellar space
We have already explored how to reach interstellar objects (similar to 1I and 2I) via Project Lyra. What we wanted to find out in our most recent work is whether we can launch a spacecraft towards a nomadic world using existing or near-term technology and reach it within a few decades or less. In particular, we wanted to find out whether we could reach nomadic worlds that are potentially life-bearing. Some authors have posited that nomadic worlds larger than 100 km in radius may host subsurface oceans with liquid water (Abramov & Mojzsis, 2011), and larger nomadic planets certainly should be able to do this. Now, although small nomadic worlds have not yet been detected, we can estimate how far such a 100 km-size object is from the solar system on average. We do so by interpolating the average distance of various objects in interstellar space, ranging from exoplanets to interstellar objects and interstellar dust. The size of these objects spans about 13 orders of magnitude. The result of this interpolation is shown in Fig. 2. We can see that ~100 km-sized objects have an average distance of about 2000 times the distance between the Sun and the Earth (known to astronomers as the astronomical unit, or AU).
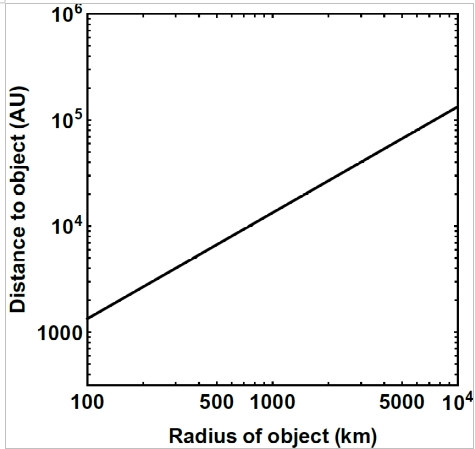
Fig. 2: Radius of nomadic world versus the estimated average distance to the object
This is a fairly large distance, over 400 times the distance to Jupiter and about five times farther away than the putative Planet 9 (~380 AU) (Brown & Batygin, 2021). It is important to keep in mind that this is a rough statistical estimate for the average distance, meaning that the ~100 km-sized objects might be discovered much closer or farther away than the estimate. However, in the absence of observational data, such an estimate provides us with a starting point for exploring the question of whether a mission to such an object is feasible.
We use such estimates to investigate further whether a spacecraft with an existing or near-term propulsion system may be capable of reaching a nomadic world within a timeframe of 50 years. The result can be seen in Table 1.
Table 1: Average radius of nomadic world reachable with a given propulsion system in 50 years
It turns out that chemical propulsion combined with various gravity assist maneuvers is not able to reach such objects within 50 years. Solar sails and magnetic sails also fall short, although they come close (~75 km radius of nomadic object).
However, electric sails seem to be able to reach nomadic worlds close to the desired size and already have a reasonably high technology readiness level. Electric sails exploit the interaction between charged wires and the solar wind. The solar wind consists of various charged particles such as protons which are deflected by the electric field of the wires, leading to a transfer of momentum, thereby accelerating the sail. Proposed by Pekka Janhunen in 2004 (Janhunen, 2004), electric sails have also been considered for interplanetary travel and even into interstellar space (Quarta & Mengali, 2010; Janhunen et al., 2014). Up to 25 astronomical units (AU) per year seem to be achievable with realistic designs (Janhunen & Sandroos, 2007). Electric sail prototypes are currently being prepared for in-space testing (Iakubivskyi et al., 2020). Previous attempts to deploy an electric sail by the ESTCube-1 CubeSat mission in 2013 and Aalto-1 in 2022 were not successful (Slavinskis et al., 2015; Praks et al., 2021).
It turns out that more advanced propulsion systems are required, if we want to have a statistically good chance of reaching nomadic worlds significantly larger than 100 km radius. Laser electric propulsion and magnetoplasmadynamic (MPD) thrusters would get us to objects of 150 and 230 km respectively. Laser electric propulsion uses lasers to beam power to a spacecraft with an electric propulsion system, thereby removing a key bottleneck of providing power to an electric propulsion system in deep space (Brophy et al., 2018). MPD thrusters would be capable of providing high specific impulse and/or high thrust (the VASIMR engine is an example), although it remains to be seen how sufficient power can be generated in deep space or sufficient velocities be reached in the inner solar system by solar power.
Reaching even larger objects (i.e., getting to significantly further distances) requires propulsion systems which are potentially interstellar capable: nuclear fusion and laser sails, as the closest such objects might be at distances of as much as a light year off. These propulsion systems could even reach nomadic worlds of a similar size as Earth, nomadic worlds comparable to those we have already discovered. The average distance to such objects should still be a few times smaller than the distance to other star systems (~105 AU from the solar system, versus Proxima Centauri, for example, at about 270,000 AU). Hence, it is no surprise that the propulsion systems (fusion and laser sail) have a sufficient performance to reach large nomadic planets in less than 50 years, although the maturity of these propulsion system is at present fairly low.
Laser electric propulsion and MPD propulsion are also on the horizon, although there are significant development challenges ahead to reach sufficient performance at the system level, integrated with the power subsystem.
What does this mean? The first conclusion we draw is that while we develop more and more advanced propulsion systems, we become capable of reaching larger and larger (and potentially more interesting) objects in interstellar space. At present, electric sails appear to be the most promising propulsion system for nomadic planet exploration, possessing sufficient performance and a reasonably high maturity at the component level.
Second, instead of seeing interstellar space as a void with other star systems as the only relevant target, we now have a quasi-continuum of exploration-worthy objects at different distances beyond the boundary of the solar system. While star systems have been “first-class citizens” so far with no “second-class citizens” in sight, we might now be in a situation where a true class of “second-class citizens” has emerged. Finding these close nomads will be a technological and observational challenge for the next few decades.
Third, and this might be controversial, the boundary defining interstellar travel is destabilized. While traditionally interstellar travel has been treated primarily as travel from one star system to another, we might need to expand its scope to include travel to the “in-between” objects. This would include travel to aforementioned objects, but we might also discover planetary systems associated with free-floating brown dwarfs. It seems likely that nomadic worlds are orbited by moons, similar to planets in our solar system. Hence, is interstellar travel if and only if we travel between two stars, where stars are objects maintaining sustained nuclear fusion? How shall we call travel to nomadic worlds then? Shall we call this type of travel “transstellar” travel, i.e. travel beyond a star, or in-between-stellar travel?
Furthermore, nomadic worlds have likely formed in a star system of origin (although they may have formed at the end, rather than at the beginning, of the stellar main sequence). To what extent are we visiting that star system of origin by visiting the nomadic world? Inspecting a souvenir from a faraway place is not the same as being at that place. Nevertheless, the demarcation line is not as clear as it seems. Are we visiting another star system if and only if we visit one of its gravitationally bound objects? While these are seemingly semantic questions, they also harken back to the question of why we are attempting interstellar travel in the first place. Is traveling to another star an achievement by itself, is it the science value, or potential future settlement? Having a clearer understanding of the intrinsic value of interstellar travel may also qualify how far traveling to interstellar objects and nomadic worlds is different or similar.
We started this article with the analogy of driftwood between islands. While the interstellar community has been focusing mainly on star systems as primary targets for interstellar travel, we have argued that the existence of interstellar objects and nomadic worlds opens entirely new possibilities for missions between the stars, beyond an individual star system (in-between-stellar or transstellar travel). The driftwood may become by itself a worthy target of exploration. We also argued that we may have to revisit the very notion of interstellar travel, as its demarcation line has been rendered fuzzy.
References
Abramov, O., & Mojzsis, S. J. (2011). Abodes for life in carbonaceous asteroids?. Icarus, 213(1), 273-279.
Bannister, M. T., Bhandare, A., Dybczy?ski, P. A., Fitzsimmons, A., Guilbert-Lepoutre, A., Jedicke, R., … & Ye, Q. (2019). The natural history of ‘Oumuamua. Nature astronomy, 3(7), 594-602.
Brophy, J., Polk, J., Alkalai, L., Nesmith, B., Grandidier, J., & Lubin, P. (2018). A Breakthrough Propulsion Architecture for Interstellar Precursor Missions: Phase I Final Report (No. HQ-E-DAA-TN58806).
Brown, M. E., & Batygin, K. (2021). The Orbit of Planet Nine. The Astronomical Journal, 162(5), 219.
de León, J., Licandro, J., Serra-Ricart, M., Cabrera-Lavers, A., Font Serra, J., Scarpa, R., … & de la Fuente Marcos, R. (2019). Interstellar visitors: a physical characterization of comet C/2019 Q4 (Borisov) with OSIRIS at the 10.4 m GTC. Research Notes of the American Astronomical Society, 3(9), 131.
Hein, A. M., Eubanks, T. M., Lingam, M., Hibberd, A., Fries, D., Schneider, J., … & Dachwald, B. (2022). Interstellar now! Missions to explore nearby interstellar objects. Advances in Space Research, 69(1), 402-414.
Iakubivskyi, I., Janhunen, P., Praks, J., Allik, V., Bussov, K., Clayhills, B., … & Slavinskis, A. (2020). Coulomb drag propulsion experiments of ESTCube-2 and FORESAIL-1. Acta Astronautica, 177, 771-783.
Janhunen, P. (2004). Electric sail for spacecraft propulsion. Journal of Propulsion and Power, 20(4), 763-764.
Janhunen, P., Lebreton, J. P., Merikallio, S., Paton, M., Mengali, G., & Quarta, A. A. (2014). Fast E-sail Uranus entry probe mission. Planetary and Space Science, 104, 141-146.
Janhunen, P., & Sandroos, A. (2007, March). Simulation study of solar wind push on a charged wire: basis of solar wind electric sail propulsion. In Annales Geophysicae (Vol. 25, No. 3, pp. 755-767). Copernicus GmbH.
Jewitt, D., & Seligman, D. Z. (2022). The Interstellar Interlopers. arXiv preprint arXiv:2209.08182.
Lingam, M., & Loeb, A. (2019). Subsurface exolife. International Journal of Astrobiology, 18(2), 112-141.
Praks, J., Mughal, M. R., Vainio, R., Janhunen, P., Envall, J., Oleynik, P., … & Virtanen, A. (2021). Aalto-1, multi-payload CubeSat: Design, integration and launch. Acta Astronautica, 187, 370-383.
Quarta, A. A., & Mengali, G. (2010). Electric sail mission analysis for outer solar system exploration. Journal of guidance, control, and dynamics, 33(3), 740-755.
Slavinskis, A., Pajusalu, M., Kuuste, H., Ilbis, E., Eenmäe, T., Sünter, I., … & Noorma, M. (2015). ESTCube-1 in-orbit experience and lessons learned. IEEE aerospace and electronic systems magazine, 30(8), 12-22.
Westphal, A. J., Stroud, R. M., Bechtel, H. A., Brenker, F. E., Butterworth, A. L., Flynn, G. J., … & 30714 Stardust@ home dusters. (2014). Evidence for interstellar origin of seven dust particles collected by the Stardust spacecraft. Science, 345(6198), 786-791.

A Role for Comets in Europa’s Ocean?
The role comets may play in the formation of life seems to be much in the news these days. Following our look at interstellar comets as a possibly deliberate way to spread life in the cosmos, I ran across a paper from Evan Carnahan (University of Texas at Austin) and colleagues (at JPL, Williams College as well as UT-Austin) that studies the surface of Europa with an eye toward explaining how impact features may evolve.
Craters could be cometary in origin and need not necessarily penetrate completely through the ice, for the team’s simulations of ice deformation show drainage into the ocean below from much smaller events. Here comets as well as asteroids come into play as impactors, their role being not as carriers of life per se but as mechanisms for mixing already existing materials from the surface into the ocean.
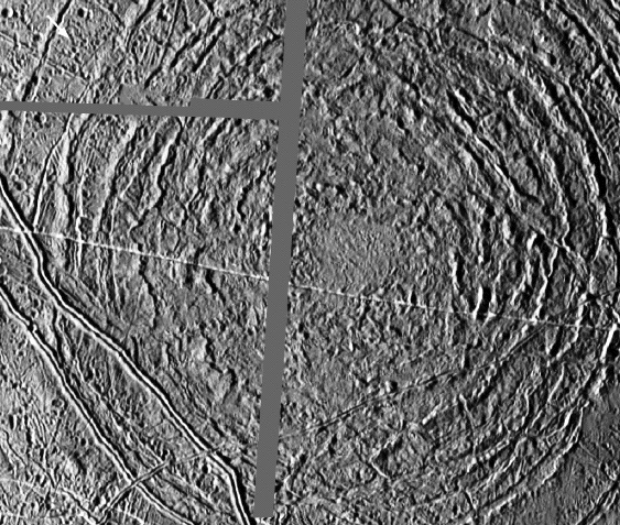
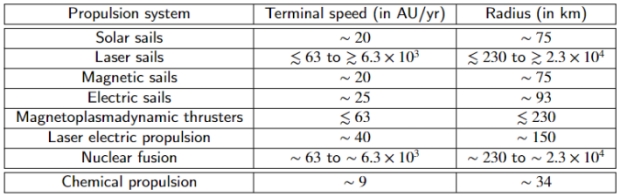
Image: Tyre, a large impact crater on Europa. Credit: NASA/JPL/DLR.
That, of course, gets the attention, for getting surface oxidants produced by solar irradiation through the ice has been a challenge to the idea of a fecund Europan ocean. The matter has been studied before, with observational evidence for processes like subduction, where an ice surface moves below an adjacent sheet, and features that could be interpreted as brine drainage, where melting occurs near the surface, although this requires an energy source that has not yet been determined. But many craters show features suggestive of frozen meltwater and post-impact movement of meltwater beneath the crater.
The Carnahan paper notes, too, how many previous studies have been done on impacts that penetrate the ice shell and directly reach the ocean, which would move astrobiologically interesting materials into it, but while impacts would have been common in the history of the icy moon, the bulk of these may not have been penetrating. Much depends upon the thickness of the ice, and on that score we await data from future missions like Europa Clipper and JUICE to probe more deeply. Current thinking seems to be coalescing around the idea that the ice is tens of kilometers thick.
The authors believe that impacts need not fully penetrate the ice to have interesting effects. Such impacts should produce melt chambers, some of them of considerable size, allowing heated meltwater to then sink through the ice remaining below them. This meltwater mechanism copes with a thick ice shell and does not require that it actually be penetrated to mix surface ingredients with the water below. The observational evidence can support this, not only on Europa but elsewhere. Implicit in the discussion is the idea that the ice surrounding a melt chamber is not rigid. From the paper:
…impacts that generate melt chambers also significantly warm and soften the surrounding ice making it susceptible to viscous deformation. Furthermore, although not explored here, the impact may generate fractures that allow for transport of melts short distances away from the crater melt pond… Importantly, the crater record of icy moons includes craters of varying complexities (Schenk, 2002; Turtle & Pierazzo, 2001) with anomalous features such as collapsed pits, domes, and central Massifs that imply post-impact modifications (Bray et al., 2012; Elder et al., 2012; Korycansky, 2020; Moore et al., 2017; Silber & Johnson, 2017; Steinbrügge et al., 2020). These observed crater features suggest that both impact structures and the generated melts experience significant post-impact evolution that has so far received little attention.
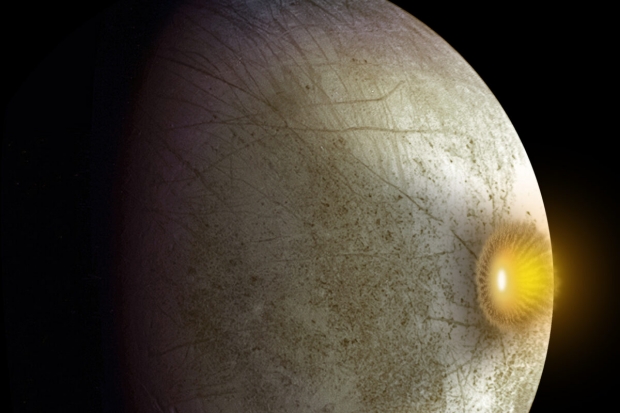
Image: An artist’s concept of a comet or asteroid impact on Jupiter’s moon Europa. Credit: NASA/JPL-Caltech.
The method here is to deploy mathematical simulations to study the evolution of these melt chambers on Europa. The term is ‘foundering,’ which is the movement of meltwater through the ice as it potentially transports oxidants below. If surface ice can be transferred into the ocean in a sustained way, and thus not just through massive impacts but through a range of smaller ones, the chances of developing interesting biology below only increase. The work also implies that Europa’s so-called ‘chaos’ terrain, which some have explained as the result of meltwater near the surface, may have other origins, for in this model most of the meltwater does not remain near the surface. Says Carnahan: “We’re cautioning against the idea that you could maintain very large volumes of melt in the shallow subsurface without it sinking.”
The researchers modeled comet and asteroid impacts using a shock-physics cratering simulation and massaged the output by factoring in both the sinking of dense meltwater and its refreezing within the ice shell. The modeling required analysis of the energies involved as well as the deformation of the surface ice after impact. UT’s Carnahan developed the ice shell convection model that the authors extended to match the geometry of surface impact simulations and subsequent changes in the ice.
The conclusions are striking:
Our simulations show that impacts that generate significant melt chambers lead to substantial post-impact viscous deformation due to the foundering of the impact melts. If the transient cavity depth of the impact exceeds half the ice shell thickness the impact melt drains into the underlying ocean and forms a continuous surface-to-ocean porous column. Foundering of impact melts leads to mixing within the ice shell and the transfer of melt volumes on the order of tens of cubic kilometers from the surface of Europa to the ocean.
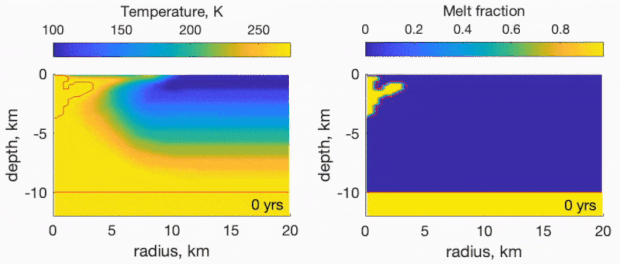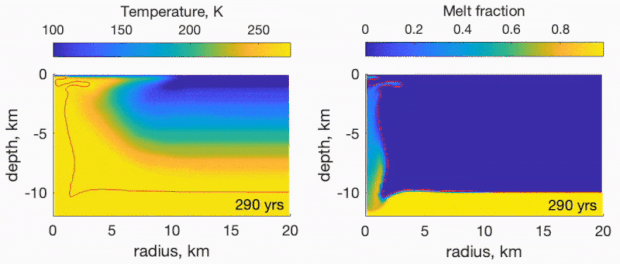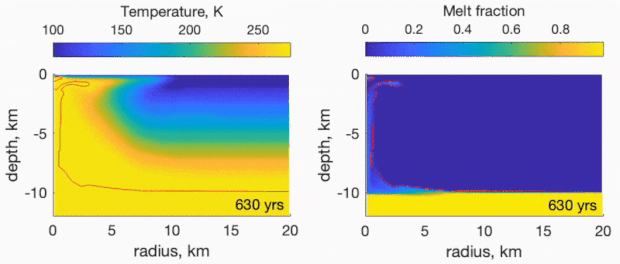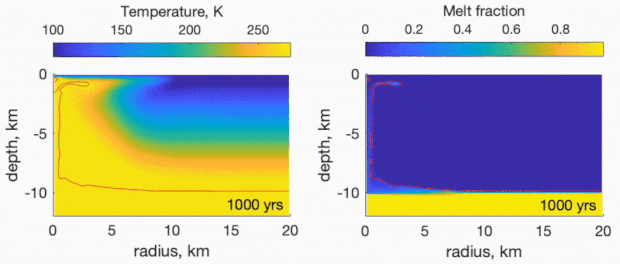
Image: A computer-generated simulation of the post-impact melt chamber of Manannan Crater, an impact crater on Europa. The simulation shows the melt water sinking to the ocean within several hundred years after impact. Credit: Carnahan et al.
So we have a way to get surface materials through to the Europan ocean, a method that because it does not require large impacts, has likely been widespread throughout Europa’s history. It’s interesting to speculate on how this process could leave evidence beyond what we’ve already uncovered in the craters visible on the surface and what corroboration in support of the analysis Europa Clipper and JUICE may be able to provide. Other icy worlds come to mind here as well, with the authors mentioning Titan as a place where even an exceedingly thick ice shell may still be susceptible to exchanging material with the surface.
Given how little we know about abiogenesis, it’s conceivable not only that life might develop under Europan ice, but that icy moons elsewhere in the Solar System may hold far more life in the aggregate than exists in what we view as the habitable zone. If that is the case, then the argument that life is ubiquitous in the universe receives strong support, but it will take a lot of hard exploration to find out, a process of discovery whose next steps via Europa Clipper and JUICE will represent only a beginning.
The paper is Carnahan et al., “Surface-To-Ocean Exchange by the Sinking of Impact Generated Melt Chambers on Europa,” Geophysical Research Letters Vol. 49, Issue 24 (28 December 2022). Full text.

The Ethics of Directed Panspermia
Interstellar flight poses no shortage of ethical questions. How to proceed if an intelligent species is discovered is a classic. If the species is primitive in terms of technology, do we announce ourselves to it, or observe from a distance, following some version of Star Trek‘s Prime Directive? One way into such issues is to ask how we would like to be treated ourselves if, say, a Type II civilization – stunningly more powerful than our own – were to show up entering the Solar System.
Even more theoretical, though, is the question of panspermia, and in particular the idea of propagating life by making panspermia a matter of policy. Directed panspermia, as we saw in the last post, is the idea of using technology to spread life deliberately, something that is not currently within our power but can be reasonably extrapolated as one path humans might choose within a century or two. The key question is why we would do this, and on the broadest level, the answer takes in what seems to be an all but universal assumption, that life in itself is good.

Image: Can life be spread by comets? Comet 2I/Borisov is only the second interstellar object known to have passed through our Solar System, but presumably there are vast numbers of such objects moving between the stars. In this image taken by the NASA/ESA Hubble Space Telescope, the comet appears in front of a distant background spiral galaxy (2MASX J10500165-0152029, also known as PGC 32442). The galaxy’s bright central core is smeared in the image because Hubble was tracking the comet. Borisov was approximately 326 million kilometres from Earth in this exposure. Its tail of ejected dust streaks off to the upper right. Credit: ESA/Hubble.
How Common is Life?
Let’s explore how this assumption plays out when weighed against the problems that directed panspermia could trigger. I turn to Christopher McKay, Paul Davies and Simon Worden, whose paper in the just published collection Interstellar Objects in Our Solar System examines the use of interstellar comets to spread life in the cosmos. An entry point into the issue is the fi factor in the Drake Equation, which yields the fraction of planets on which life appears.
We need to know whether life is present in any system to which we might send a probe to seed new life forms – major problems of contamination obviously arise and must be avoided. If we assume a galaxy crowded with life, we would not send such missions. Directed panspermia becomes an issue only when we are dealing with planets devoid of life. To the objection that everything seems to favor life elsewhere because we couldn’t possibly live in the only place in the universe where life exists, the answer must be that we have no understanding of how life began. Abiogenesis remains a mystery and the cosmos may indeed be empty.
We live in the fascinating window of time in which our civilization will begin to get answers on this, particularly as we probe into biomarkers in exoplanet atmospheres and conceivably discover other forms of life in venues like the gas giant moons. But we don’t have such answers yet, and it is sensible to point out, as the authors do, that the Principle of Mediocrity, which suggests that there is nothing special about our Solar System or Earth itself, is a philosophical argument, not one that has been proven by science. We have no idea if there is life elsewhere, even if many of us hope it is there.
Protecting existing life is paramount, and the authors point to the planetary protection issues we face in terraforming Mars, the latter being a local kind of directed panspermia. They cite the basic principle: “…planetary protection would dictate that life forms should not be introduced, either in a directed mode or through random processes, to any planet which already has life.”
I like the way McKay, Davies and Worden present these issues. In particular, assuming we picked out a likely planet in the habitable zone of its star, would there ever be a way to demonstrate that life does not exist on it? The answer is thorny, it being impossible to prove a negative. This gives rise to the possibilities the authors consider when evaluating whether directed panspermia could be used. From the paper:
1. Life might exist on a target planet in low abundance and be snuffed out by seeding.
2. Alien life might be abundant on a planet but present unfamiliar biosignatures yielding a false negative.
3. A comet might successfully seed a barren target planet but go on to contaminate others that already host life, either in the same planetary system or another. The long-term trajectory of a comet is almost impossible to predict.
4. Even if terrestrial life does not directly engage with alien life, it may be more successful in appropriating resources, thus driving indigenous biota to extinction by starvation
There are ways around these issues. Snuffing out life would not be likely if we seeded a protoplanetary disk rather than a fully formed world, which would also remove objection 2, for there would be no biosignatures to be had. A planet that turns out not to be barren might be saved from our seeding efforts by using some kind of ‘kill switch’ that is available to destroy the inoculated life. But all these issues loom large, so large that directed panspermia collapses unless we establish that numerous habitable but lifeless worlds do exist. If life is vanishingly rare, then a kind of galactic altruism can be invoked, seeing our species as gifted with the chance to spread life in the galaxy.
Off on a Comet
All this is dependent on advances in exoplanet characterization and research into life’s origins on Earth, but the questions are worth asking because we may, relatively soon as civilizations go, begin to learn tentative answers. It seems natural that the authors would turn to interstellar comets as a delivery vehicle of choice. Here’s a passage from the paper, examining how spores from a directed panspermia effort could be spread through passing comets by the injection of a biological inoculum into comets whose trajectories are hyperbolic or could otherwise be modified. Such objects need not impact another planet but could be effective simply passing through their stellar system:
These small particles are subsequently shed as the comet passes through systems that have, or will form into, suitable planets, such as protostellar molecular clouds, planet-forming nebulae around stars, and recently formed planetary systems. The comets themselves are unlikely to be gravitationally captured or collide as they move through star systems… but the small dust particles released by the comet—as observed in 2I/Borisov—will be captured. Particles measuring a few 10s to 100s microns in radius are large enough to hold many microorganisms but small enough to enter a planetary atmosphere without significant heating.

Image: This artist’s impression shows the first interstellar object discovered in the Solar System, `Oumuamua. Note the outgassing the artist inserts into the image as a subtle cloud being ejected from the side of the object facing the Sun. Credit: ESA/Hubble, NASA, ESO, M. Kornmesser.
The focus on comets is natural in the era of ‘Oumuamua and 2I/Borisov, and the expectation is widespread that we will be learning of interstellar objects in huge numbers moving through the Solar System as we expand our observing efforts. Why not hitch a ride? There is every expectation that the inoculum injected into a comet could survive the journey, to one day settle into a planetary atmosphere. Thus:
One meter of ice reduces the radiation dose by about five orders of magnitude… In a water-rich interstellar comet, internal radiation from long-lived radioactive elements (U, Th, K) would be expected to be less than crustal levels on the Earth. In such an environment, known terrestrial organisms might remain viable for tens to hundreds of millions of years. We can also take into account advances in gene editing and related technologies that might enable psychrophiles, which are able to very slowly metabolize and repair genetic damage at temperatures as low as-40°C…, to ”tick over,” although slowly, at still lower temperatures. That would enable them to remain viable for even longer durations.
The time scales for delivering an inoculum to an exoplanet are mind-boggling, on the order of 105 to 106 years just to pass near another stellar system. The authors point out that given the hyperbolic velocity of 2I/Borisov, it would take the comet approximately 40,000 years to travel the distance to Alpha Centauri, and 500 million years to travel the distance of the Milky Way’s radius. Indeed, the most likely previous encounter of ‘Oumuamua with another star occurred 1 million years ago.
Perhaps orbital interventions when seeding the comet could alter its trajectory toward specific stars, to avoid the random nature of the seeding program. And I think they would be necessary: Random trajectories might well take our comet into stellar systems with living worlds that we know nothing about. Thus the authors’ point #3 above.
The Rhythms of Panspermia
Clearly, directed panspermia by interstellar comet is for the patient at heart. And as far as I can see, it’s also something a civilization would do completely out of philosophical or altruistic motives, for there is no conceivable return from mounting such an effort beyond the satisfaction of having done it. I often address questions of value that extend beyond individual lifetimes, but here we are talking about not just individual but civilizational lifetimes. Is there anything in human culture that suggests an adherence to this kind of ultra long-range altruism? It’s a question I continue to mull over on my walks. I’d also appreciate pointers to science fiction treatments of this question.
There is an interesting candidate for directed panspermia close to the Sun: Epsilon Eridani. Here we have a youthful system, thought to be less than a billion years old, with two debris belts and two planets thus far discovered, one a gas giant, the other a sub-Neptune. If there is a terrestrial-class world in the habitable zone here, it would be a potential target for a life-bearing mission. So too might a Titan-class world, which raises the interesting question of whether different types of habitability should be considered. We may well find exotic life not just on Titan but also under the ice of Europa, giving us three starkly different possibilities. Would a directed panspermia effort be restricted to terrestrial class worlds like Earth?
Whatever our ethical concerns may be, directed panspermia is technologically feasible for a civilization advanced enough to manipulate comets, and thus we come back to the possibility, discussed decades ago by Francis Crick and Leslie Orgel, that our own Solar System may have been seeded for life by another civilization. If this is true, we might find evidence of complex biological materials in comet dust. We would also, as the authors point out, expect life to be phylogenetically related throughout the Solar System, whether under Europan ice or on the surface of Mars or indeed Earth.
Always complicating such discussions is the possibility of natural panspermia establishing life widely through ejecta from early impacts, so we are in complex chains of causation here. We’re also in the dense thicket of human ethics and aspiration. Let’s assume, as the authors do, that directed panspermia is out for any world that already has life. But if life is truly rare, would humanity have the sense of obligation to embark on a program whose results would never be visible to its creators? We cherish life, but where do we find the imperative to spread it into a barren cosmos?
I’ll close with a lengthy passage from Olaf Stapledon, a frequent touchstone of mine, who discussed “the forlorn task of disseminating among the stars the seeds of a new humanity” in Last and First Men (1930):
For this purpose we shall make use of the pressure of radiation from the sun, and chiefly the extravagantly potent radiation that will later be available. We are hoping to devise extremely minute electro-magnetic “wave-systems,” akin to normal protons and electrons, which will be individually capable of sailing forward upon the hurricane of solar radiation at a speed not wholly incomparable with the speed of light itself. This is a difficult task. But, further, these units must be so cunningly inter-related that, in favourable conditions, they may tend to combine to form spores of life, and to develop, not indeed into human beings, but into lowly organisms with a definite evolutionary bias toward the essentials of human nature. These objects we shall project from beyond our atmosphere in immense quantities at certain points of our planet’s orbit, so that solar radiation may carry them toward the most promising regions of the galaxy. The chance that any of them will survive to reach their destination is small, and still smaller the chance that any of them will find a suitable environment. But if any of this human seed should fall upon good ground, it will embark, we hope, upon a somewhat rapid biological evolution, and produce in due season whatever complex organic forms are possible in its environment. It will have a very real physiological bias toward the evolution of intelligence. Indeed it will have a much greater bias in that direction than occurred on the Earth in those sub-vital atomic groupings from which terrestrial life eventually sprang.
The paper is McKay, Davies & Worden, “Directed Panspermia Using Interstellar Comets,” Astrobiology Vol. 22 No. 12 (6 December 2022), 1443-1451. Full text.

Life from Elsewhere
The idea that life on Earth came from somewhere else has intrigued me since I first ran into it in Fred Hoyle’s work back in the 1980s. I already knew of Hoyle because, if memory serves, his novel The Black Cloud (William Heinemann Ltd, 1957) was the first science fiction novel I ever read. Someone brought it to my grade school and we passed the copy around to the point where by the time I got it, the paperback was battered though intact. Its cover remains a fine memory. I remember being ingenious about appearing to be reading an arithmetic text in class while actually reading the Hoyle novel.

In the book, the approach of a cloud of dust and gas in the Solar System occasions alarm, with projections of the end of photosynthesis as the Sun’s light is blocked. Even more alarming are the unexpected movements of the cloud once it arrives, which suggest that it is no inanimate object but a kind of organism.
I’ve been meaning to re-read The Black Cloud for years and this post energizes me to do just that, though this time around the old paperback will have to give way to a Kindle, as I had to pass the original back to its owner for continued circulation, after which it disappeared.
But back to panspermia. As the novel shows, Hoyle was interested not just in the nature of consciousness but likewise the matrix in which it can be embedded. By the 1980s, working with a former doctoral student named Chandra Wickramasinghe (Cardiff University), he was suggesting that dense molecular clouds could contain biochemistry, possibly concentrated in the volatiles of comets in their trillions. The notion that the inside of a comet could have become the source for life on Earth led the duo to propose that space-borne clouds might even evolve bacteria, which they explored in a 1979 book called Diseases from Space, an idea that was widely dismissed.
But leaving bacteria born in space aside, the idea that life can move between planets continues to intrigue scientists. We have, after all, objects on Earth that have fallen from the sky and turn out to have been the result of impacts on Mars. So if we can move past the question of life’s origin and focus instead on life’s propagation, panspermia takes on new life. Abiogenesis may be operational on the early Earth, but perhaps incoming materials from comets or other planets had their own unique role to play. Life in this case is not an either/or proposition but a combination of factors.
Be aware of a special issue of Astrobiology (citation below) which delves into these matters, with ten essays by the likes of Paul Davies, Fred Adams, Charles Lineweaver, as well as Avi Loeb and Ben Zuckerman, who from their own perspectives tackle the question of ‘Oumuamua as a technological object rather than a comet. The latter discussion reminds us that the discovery of interstellar comets moving through our Solar System widens the panspermia debate. Now we’re talking about the potential transfer of materials not just between planets but between stellar systems.
If panspermia does operate, meaning that life can survive space journeys lasting perhaps millions of years, then we might begin to speak of a common molecular basis for the living things we would expect to find widely in the universe. Paul Davies and Peter Worden point this out in their introduction to the special collection, noting that this view contrasts enormously with the more common view that life emerges on its own wherever suitable conditions can be found. In both cases, the implication is for a cosmos filled with life, but only panspermia argues for its natural spread between worlds.
The key word there is ‘natural.’ If panspermia does not occur via natural processes, what about the possibility of ‘directed panspermia,’ in which a civilization makes the decision to use technology to spread life as a matter of policy? It startled me in reading through these essays to realize that Francis Crick and the British chemist Leslie Orgel had proposed as far back as 1973 in a paper in Icarus that we investigate present-day organisms to see whether we can find “any vestigial traces” of extraterrestrial origins. Their paper offers this startling finish:
Are the senders or their descendants still alive? Has their star inexorably warmed up and frizzled them, or were they able to colonise a different Solar System with a short-range spaceship? Have they perhaps destroyed themselves, either by too much aggression or too little? The difficulties of placing any form of life on another planetary system are so great that we are unlikely to be their sole descendants. Presumably they would have made many attempts to infect the galaxy. If the range of their rockets were small this might suggest that we have cousins on planets which are not too distant. Perhaps the galaxy is lifeless except for a local village, of which we are one member.
I like that word ‘frizzled.’ It even gets past the spell-check!
We’ve looked at proposals for directed panspermia before in these pages, as for example in Robert Buckalew’s Engineered Exogenesis: Nature’s Model for Interstellar Colonization and my entry Directed Panspermia: Seeding the Galaxy, which focuses on Michael Mautner and Greg Matloff’s ideas on spreading life in the cosmos. Next time I want to dig into an essay from the new Astrobiology collection by Christopher McKay, Paul Davies and Simon Worden on the question of how we might use interstellar comets of the sort we now believe to be common to spread life in the galaxy.
A key question: Why would we want to do this? Or more precisely, how would we go about deciding whether spreading life into the cosmos is an ethical thing to do?
The paper we’ll look at next time is McKay, Davies & Worden, “Directed Panspermia Using Interstellar Comets,” Astrobiology Vol. 22 No. 12 (6 December 2022), 1443-1451. Full text. This is a paper in the Astrobiology special collection Interstellar Objects in Our Solar System (December 2022). The Crick and Orgel paper is “Directed Panspermia,” Icarus Vol. 19 (1973), 341-346.


