Two brown dwarfs relatively near to the Sun may be just the first such objects we’ll soon identify with data from the WISE (Wide-field Infrared Survey Explorer) satellite. Ralf-Dieter Scholz (Leibniz-Institut für Astrophysik, Potsdam) and colleagues have gone to work on a search for brown dwarfs with high proper motion, looking for brown dwarfs in the immediate solar neighborhood using not just the preliminary WISE data release but the previous near-infrared (2MASS) and deep optical (SDSS) surveys. The search has already begun to pay off.
The two brown dwarf discoveries — WISE J0254+0223 and WISE J1741+2553 — are at estimated distances of 15 and 18 light years respectively. Their strong infrared signature and their extremely faint appearance at visible wavelengths attracted the team’s attention, and both show the high proper motion across the sky that flags nearby stellar objects. The team was able to use the Large Binocular Telescope (LBT) in Arizona to determine spectral type and distance more accurately. Interestingly, both objects fit into the category of T-type brown dwarfs, at the boundary of the still not well defined class of Y-type brown dwarfs.
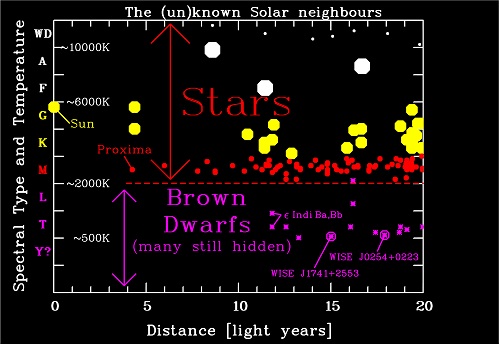
Image: The (un)known Solar neighbors. The stars are shown with symbols of different sizes and colours, roughly corresponding to their real sizes and spectral types. Most stars in the Solar neighborhood are red dwarf stars of spectral type M (in the middle of the figure) with surface temperatures of slightly more than 2000 Kelvin. Proxima, our nearest known neighbor, also belongs to this class. The number of brown dwarf discoveries (almost all with spectral types L and T, and surface temperatures below 2000 K) is already higher than the number of white dwarfs (shown as small white dots at the top). The two nearest brown dwarfs, epsilon Indi Ba and Bb, the discovery of which was reported by the AIP in 2003 and 2004, and the newly found objects are marked. (Credit: AIP).
Do brown dwarfs, hitherto undetected, surround us in large numbers? We certainly can’t rule out the possibility, and we can expect much more data mining from the riches WISE has accumulated. And yes, the case for a brown dwarf closer than the Alpha Centauri stars is still open, making the brown dwarf hunt of unusual interest for identifying potential targets for future probes. But the two brown dwarfs in question could prove useful in many ways in their own right, as the paper on this work notes:
While WISE J0254+0223 and WISE J1741+2553 are likely similar to the few other T8-T10 brown dwarfs known, they are the first ultracool brown dwarfs detected in both 2MASS and SDSS. With their relatively bright magnitudes they are excellent targets for detailed spectroscopic investigations and for high resolution imaging in search of possible binarity. They may become important laboratory sources at the boundary between the T-type and the suggested Y-type (Kirkpatrick et al. 1999) classes of brown dwarfs.
Image: False-colour images of the two brown dwarf discoveries WISE J0254+0223 and WISE J1741+2553 (composite of three images taken by the Wide-field Infrared Survey Explorer (WISE) with different filters in the infrared). In the WISE colours, the extremely cool brown dwarfs appear as yellow-green objects. The positions of the objects as observed by a previous near-infrared sky survey about ten years before the WISE observations are also marked. Every image covers a sky field about 200 times smaller than the full moon. After 700 and 1200 years, respectively, the proper motions of the two objects lead to a shift in their position as large as the full moon diameter. (Credit: AIP, NASA/IPAC Infrared Science Archive).
The paper is Scholz et al., “Two very nearby (d ~ 5 pc) ultracool brown dwarfs detected by their large proper motions from WISE, 2MASS, and SDSS data” (preprint).




Michael Simmons, if there were repulsive forces at certain distances for solar mass objects gravity would not be a conservative force. I can see how this might not matter on a scale beyond that of a galaxy, but surely it would create sever problems if it occurred both within a galaxy and to such an extent that it noticeably effected the distribution of stars. If you crank MOND up that much, surely it must give galaxies a tendency to either expand of shrink with time, save for those on the knife’s edge of certain parameters.
ENIAC, if the mechanism I speak of has any significant at all to these shells, we find that the first one is at 11 light years, the one at 4 light years being obviously due to the first effect that I spoke of in my comment on July 28 (note that the “group” at 4ly is actually a single data point).
Additionally this effect must scales as per the gravitational potential which is proportional to (solar mass + mass of surveyed star) / radius. One way to think of this is that gravitational acceleration scales as (star+sun) / R^2, but the time a passing star takes to transverse this sphere of influence is proportional to the radius of that inferred zone of influence, and both effects combined produce the above scaling. I suspect that in a new chart plotting distance per combined mass against star mass will show that red dwarfs join the first shell.
Eniac: imagine you have two stars of equal mass passing by each other. Their paths will bend together. They will accelerate whilst approaching and decelerate after the closest point. Their paths are deflected from their original paths.
Gravity causes them to spend longer nearer to each other than would be the case if there were no gravity. There would not be any shell effect caused by Rob’s mechanism. It is the REVERSE of that.
The liquid phase molecules are a poor analogy to stellar dynamics. This is because liquid-phase moleculs are large compared to their separation distances and intermolecular binding forces exceed the average molecular energy.
The gas phase is the model to use. An ideal gas has no intermolecular forces and the individual molecules take up negligible volume. The simple gas laws follow from this. In a REAL gas, there ARE intermolecular (van der Waals) forces, which we can equate to gravity between stars. This modifies the ideal gas behaviour and the deviation from non-ideal behaviour is increased by lower temperature and higher pressure.
In the galactic disk, this departure from non-ideal behaviour will be happening, but I suspect the situation is not far from ideal. I bit like the gases in our atmosphere, where the departure from non-ideality can be neglected in ordinary uses.
“imagine you have two stars of equal mass passing by each other. Their paths will bend together. They will accelerate whilst approaching and decelerate after the closest point. Their paths are deflected from their original paths. Gravity causes them to spend longer nearer to each other than would be the case if there were no gravity.”
That is a great start kzb, but then you leap to an incorrect conclusion. Actually this is just a restatement of point 1) that I made on 28 July. Try calculating the extra time in total that such a star spends in the zone where Sol influence predominates, and not just its extra proximity and you will get a shock. Think of a brown dwarf approaching Sol 10 times more closely than it would otherwise. By conservation of angular momentum, it must have accelerated to 10 times its previous relative speed at perihelion, and for a much longer it must be travelling twice its normal speed. Its extra curved path can not make up for this since its shape is just hyperbolic . Actually similar arguments can be made for every point along its perturbed trajectory, so a detailed calculation is unnecessary.
I feel that for the sake of completeness I should also prove the first effect:
1) When a random vacant position is compared to a star filled one, we will see that a star will more frequently have a “very close” (but unbound) stellar neighbour than expected,
Consider just the paths of the closest stars to another star, and how its position is perturbed by the presence of that star. Now think of how their proximity to that star might be altered by a factor F to that which it might otherwise be. This would have the effect of increasing the density of stars at the level of the new proximity by a factor of F^3 from normal. By conservation of angular momentum this would then speed through this area at F times the velocity that it would have otherwise, thus reducing the density of stars like it there because the reduced time that they spend there, by roughly 1/F. This is still an increase of F^2 to the stellar density of regions that are so close in that they would not be expected to contain a neighbour.
kzb, here’s a conundrum for you, imagine a universe that looks just like ours and in which gravity is also a conservative force, yet it works in such a way that a star in a galaxy of originally randomly distributed stars will tend to attract others in such a way that at every radius it tends to have more neighbours than a random spot in this galaxy. Sure, this means that the stars here have to have higher velocities because gravitational + kinetic energy are conserved, but this extra kinetic energy is irrelevant to the stars outside this region. They just see a big clump of stars and get drawn into it. What can stop galaxies in this universe from being prone to spontaneous collapse?
I suppose a pendulum spends more time near its high points than it does near its low point, so if I think of it like that it makes more sense.
The only way I’d be able to calculate it would be via spreadsheet, calculate time between points in trajectory and separation distance both with and without gravitational attraction. So quite a long job.
HOWEVER, if this mechanism is significant, how come you don’t see the same pattern in the red dwarfs?
Rob Henry, you are describing our universe and I claim my $1m.
What stops everything collapsing is kinetic energy exceeding the binding energy. If you could extract most of the kinetic energy from the stellar population, it would indeed collapse.
Elliptical galaxies and globular clusters are in virial equilibrium. So is a spiral galaxy disk, except from the perspective of a star orbiting within the disc, the attraction appears to be towards the mid-plane of the disc rather than to a central point.
Kzb, this effect scales as per gravitational attraction which is directly proportional to the mass of the sun PLUS the neighbouring star. If you adjust for this several join the first shell at 11 light years, but I still feel that it needs much hand-waving to explain the outer shells (if indeed these others are real).
Note that it is best to replot against distance cubed so that a random distribution should spread evenly.
Kzb, I will hold off your million till you address the relevant point, which you did not above. It is true that if kinetic energy exceeds binding energy, then an ISOLATED clump of matter must EVENTUALLY disburse. Here the added condition to the rules of our universe is equivalent to stating that that disbursal time is significantly longer than the time that it takes to attract new matter into that shell of influence! IT MUST STILL COLLAPSE
Rob Henry, I’m afraid the mathematics of virial equilibrium are well beyond my capabities. But your reasoning cannot be correct, because it allows only two final outcomes, either collapse or dispersal. Since globular clusters and elliptical galaxies are observed, and they are stable structures over cosmological timescales, we know that long-term equilibrium can and often is established.
Also I suspect we are being tripped up by terminology. By “binding energy” I meant between two individual particles. If the kinetic energy exceeds the binding energy of the structure AS A WHOLE, then agreed the particles will disipate.
So when we see a galaxy or globular cluster, we are seeing a collection of particles whose kinetic energy exceeds the inter-particle binding energy but does not exceed the binding energy of the whole galaxy or cluster.
I now realised that my analysis has been remise at examining the effects of the bulk of stars with each other.
Firstly, if the motions of stars in the examined field are in equilibrium (ie if there has not been a recent injection of new stars into our part of the galaxy, and if a wave of altered stellar density/velocity is not currently passing over our region) then the typical stellar velocities are set by elastic interactions between the particles as in an ideal gas, so typical velocities of stars when compared to the background average, might be expected to scale inversely to the root of their masses. This would be yet another reason why red dwarfs are less effected by the earlier discussed mechanism.
Secondly, setting the typical velocities of stars in this way would ensure that relative velocities of average mass stars are not too fast for the examined effect to play a role in creating shells.
Thirdly , if significant cavities are created then even very high mass systems of stars cannot “back off’ from other stars much further than the average separation between stars, creating a maximum distance at which stars of all masses join the common shell.
Actually, I would like to also add, that while I still stand by every facet of every factor that I have presented so far, I can’t believe that the effect is really strong enough to show-up as clearly as it seems to have.
Rob Henry: I think you hit the nail on the head with your last sentence. There is no way this miniscule effect (if it operates at all) could give such a strong pattern.
I must say I don’t really understand stellar dynamics. I was thinking last night, if this pendulum effect is important, why is the stellar disk not hollow?
Stars are bobbing up and down through the galactic mid-plane. Their maximum velocity component in the z-axis will occur at the mid-plane, and their minimum velocity at the greatest distance from the plane. So you’d expect the disk to have a mid-plane minimum in stellar density. But in reality density is greatest at the mid-plane and reduces “up” or “down” as a natural log plot.
Possibly most stars have only a small velocity in the z-axis so that is the explanation.
Kzb, I would like to share with you, that which I think a miracle. I find it amazing that some interstellar clouds can dissipate enough energy to form globular clusters in the first place – while gravity effectively acts the opposite way. Note that the net gravitational effect of other stars passing through open clusters is to disburse them – and not to tighten their gravitational effect.
To set some other things straight we are at times discussing 3 very different sorts of attraction. Pendulums attract as per distance from centre point squared, stars attract each other according to the inverse of this, and are attracted to the centre of the galactic plane independently of distance. Even so, your case of the bobbing stars should work if all stars shared the same velocity in the direction of the galactic axis as they crossed the galactic plane, but they do not. Only a few stars can bob really high, and some hardly bob at all, so this mitigates your “pendulum” effect.
Also note that, above I should have allowed that our galaxy is not a random field of stars, but one circulating about a gravitation centre. As a result, faster stars will “cool off” by migrating outwards, and the resulting velocity distribution with mass will thus be flatter than I suggested.
Here’s an interesting new paper. About galaxy thick disks containing a lot more stars than previously thought. (Rob Henry, notice the kind of language used in modeling the stellar disk.):
http://arxiv.org/PS_cache/arxiv/pdf/1108/1108.0037v1.pdf
Yes I think the lack of a hollow disk is explicable, it’s just that a large component of stellar population has a low velocity dispersion.
I think it just might be the case that your effect biases star positions to a slightly non-random, more crystalline structure than a perfect gas. However I am reserving judgement because we still don’t know if the pattern is just some artifact of the plotting procedure.